

1. ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ
ЧАСТЬ 1. Спектральное представление и спектральные
характеристики периодического сигнала
ax + b, |
x [−`; 0) |
1.1. Дана кусочно-линейная функция f0(x) = ½ cx + d, |
x [0; `) |
(значения коэффициентов см. в таблице на с. 33), являющаяся математической моделью некоторого сигнала.
1.2.Продолжите эту функцию периодически на всю числовую ось, постройте график полученной периодической функции f (x) и проверьте выполнение условий Дирихле.
1.3.Постройте график функции S(x) суммы ряда Фурье.
1.4.Запишите ряд Фурье для полученной кусочно-линейной периодической функции в действительной и комплексной форме.
1.5.Запишите частичные суммы ряда Фурье S0(x), S1(x), S2(x), S3(x) и постройте их графики на одном чертеже с графиком f (x) .
1.6.Постройте амплитудную и фазовую диаграммы кусочнолинейной периодической функции (для n = 1, 2, ..., 8 ).
1.7.Запишите равенство Парсеваля и проверьте его выполнение. Найдите среднюю мощность сигнала. Запишите математический смысл равенства Парсеваля.
1.8. Продолжите функцию y1(x) = cx + d, x [0; `) периодически на всю числовую ось четным образом, запишите ряд Фурье для полученной функции в действительной и комплексной форме, постройте график S(x) суммы ряда, постройте амплитудную
ифазовую диаграммы четной функции.
1.9.Продолжите функцию y1(x) = cx+d, x [0; `) периодически на всю числовую ось нечетным образом, запишите ряд Фурье для полученной функции в действительной и комплексной форме, постройте график S(x) суммы ряда, постройте амплитудную
ифазовую диаграммы нечетной функции.
1.10.Сравните полученные в пп. 3, 8, 9 аппроксимации для функции
y1(x) = cx + d, x [0; `) и сделайте выводы.
6

ЧАСТЬ 2. Спектральное представление и спектральные
характеристики четной непериодической
|
функции |
|
|
|
|
2.1. Дан прямоугольный импульс g1(t) = ½ |
`, |
t [−`; `] |
|||
0, |
t (−2`; `) (`; 2`). |
||||
Для сравнения спектральных характеристик периодического и непериодического сигналов продолжите сначала этот импульс периодически на всю числовую ось, запишите ряд Фурье для четного периодического импульса в комплексной форме, постройте спектральную диаграмму коэффициентов Cn .
2.2. Запишите преобразование Фурье для четного прямоугольного
импульса g(t) = ½ |
`, t |
[−`; `] |
Запишите формулу для спек- |
0, t / |
[−`; `]. |
тральной плотности и постройте ее график в частотной области. Сравните график спектральной плотности непериодического импульса с огибающей спектральной диаграммы периодического импульса. Запишите, как выглядит график спектральной плотности четного сигнала.
2.3.Запишите, как изменяется спектральная плотность при увеличении амплитуды импульса g(t) в |a| раз, постройте графики нового импульса g2(t) и его спектральной плотности.
2.4.Запишите, как изменяется спектральная плотность при увели-
чении длительности импульса g2(t) в |b| раз, постройте графики нового импульса g3(t) и его спектральной плотности.
2.5.Запишите, как изменяется спектральная плотность при сдвиге
импульса g3(t) на |c| секунд по оси времени, постройте графики нового импульса g4(t) и модуля его спектральной плотности.
ЧАСТЬ 3. Спектральное представление и спектральные
характеристики произвольного
непериодического сигнала
3.1. Найдите спектральную |
dt, t 6 |
0 |
|
сигнала q(t) = ½ |
edt, t > 0 |
|
0, t < 0, |
||||
плотность |
|
|
|||
(если d < 0 ) или q(t) = ½e |
0, t < |
0, |
(если d > 0 ). Постройте гра- |
||
фики амплитудного и фазового спектров сигнала. Запишите равенство Парсеваля и проверьте его выполнение. Запишите энергетический смысл этого равенства.
7

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ.
ПЕРИОДИЧЕСКИЙ СИГНАЛ (ЧАСТЬ 1)
1.1. Пусть задана кусочно-линейная функция
f0(x) = |
½ −2x − 2, |
x [0; 3), |
(3) |
|
x − 1, |
x [−3; 0); |
|
являющаяся математической моделью некоторого сигнала.
1.2. Продолжим эту функцию периодически на всю числовую ось, получим периодическую функцию f (x) с периодом T = 2` = 6 , график которой изображен на рис. 1.
|
|
|
6f (x) |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
1 |
|
|
|
|
−6 |
µ |
|
µ |
6 |
µ - |
−9 |
U |
−3 |
U 0 |
3 |
U |
9 x |
|
|
|
−1 |
|
|
|
|
|
|
−2 |
|
|
|
Рис. 1. |
График периодически продолженной функции |
|||||
Эта функция удовлетворяет условиям Дирихле:
1)f (x) непрерывна на главном периоде [−3; 3] , за исключением конечного числа точек разрыва первого рода;
2)производная f 0(x) имеет на отрезке [−3; 3] конечное число точек разрыва первого рода.
Выполнение этих условий означает, что функция является на отрезке [−3; 3] кусочно-гладкой. Ряд Фурье кусочно-гладкой функции сходится к значению f (x) в каждой точке непрерывности функции
и к значению 12 ¡f (x−0)+f (x+0)¢ в каждой точке разрыва.
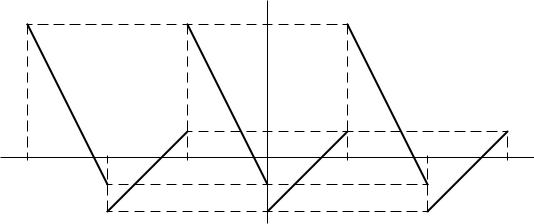
1.3. График суммы ряда Фурье приведен на рис. 2. В точках непрерывности функции график суммы ряда полностью совпадает с графиком функции. В точках разрыва первого рода значения суммы ряда отличаются от значений заданной функции и равны среднему арифметическому левого и правого пределов функции в этой точке.
8
|
|
|
|
6S(x) |
|
|
|
K |
|
K |
5 |
|
K |
|
|
r |
|
r |
|
|
r |
|
|
|
|
|
1 |
|
|
|
|
|
−6 |
µ |
|
|
µ |
6 |
µ - |
−9 |
U |
−3 |
U 0 |
3 |
U |
9 x |
|
|
r |
|
−1 |
r |
|
r |
|
|
ª |
|
ª |
|
ª |
|
|
|
|
|
−2 |
|
|
|
|
Рис. 2. |
График суммы ряда Фурье периодической функции |
||||||
1.4. Для функции f (x) , периодической с периодом T = 2` и удовлетворяющей на отрезке [−`; `] условиям Дирихле, можно записать ряд Фурье:
f (x) a0 + |
∞ |
|
|
|
|
|
|
|
|
||||||||
an cos πnx + bn sin πnx . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
n=1 |
|
|
|
` |
` |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
` |
|
|
|
πnx |
|
|
|
|
|
|||||
an = |
|
|
Z |
|
f (x) cos |
|
|
|
dx, |
n = 0, 1, 2, ...; |
|||||||
` |
|
|
` |
|
` |
|
|||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
` |
|
|
πnx |
|
|
|
|
|
|||||
bn = |
|
|
Z |
f (x) sin |
|
|
|
dx, |
n = 1, 2, ... . |
||||||||
` |
|
|
|
` |
|
||||||||||||
|
|
|
− |
` |
|
|
|
|
|
|
|
|
|
|
|||
(4)
(5)
(6)
Соотношение (4) означает, что функции f (x) соответствует ряд Фурье, записанный справа. Согласно теореме Дирихле, равенство левой и правой частей в (4) выполняется в отдельных точках. Из этого, однако, еще не следует равенство функций, т.е. что ряд в правой части (4) сходится, причем именно к f (x) . Действительно, если значения двух функций отличаются только в конечном числе точек, то интегралы (5), (6), определяющие их коэффициенты Фурье, будут одинаковыми. Такие функции имеют один и тот же ряд Фурье.
Вычислим по формулам (5), (6) коэффициенты ряда Фурье заданной функции:
9
a0 |
= 3 |
|
|
3 |
f (x)dx = 3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
(7) |
|||||||||||
|
|
|
|
|
(−2x − 1)dx + (x − 2)dx = 2 ; |
||||||||||||||||||||||||||||||||
|
|
1 |
|
Z |
|
|
|
|
|
1 |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
an = |
1 |
|
Z |
|
|
|
|
|
πnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f (x) cos |
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
(x − 2) cos |
3 |
dx = |
|
||||||||||||
|
|
|
|
(−2x − 1) cos |
|
dx + |
|
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
πnx |
|
Z |
|
|
|
πnx |
|
|
|
|
||||||||||
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
9 |
|
|
(cos πn − 1) = |
|
|
|
9 |
|
|
|
(−1)n − 1 ; |
n = 1, 2, ...; |
|
(8) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
πn)2 |
|
(πn)2 |
|
|
||||||||||||||||||||||||||||||||
bn |
= |
( |
|
|
3 |
f (x) sin πnx dx = |
|
|
|
¡ |
|
¢ |
1 |
4(−1)n − 1 . (9) |
|||||||||||||||||||||||
1 |
|
Z |
1 (4 cos πn − 1) = |
||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
πn |
|
|
|
|
|
|
|
πn |
¡ |
|
|
|
¢ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По формуле (4) запишем искомый ряд Фурье |
|
|
|
|
# . (10) |
||||||||||||||||||||||||||||||||
f (x) 4 + |
" |
|
|
|
|
π2n2 |
|
|
|
cos |
3 |
|
+ −1 +πn |
|
sin |
3 |
|||||||||||||||||||||
|
|
|
3 |
|
|
|
∞ |
¡ |
|
|
|
|
|
|
¢ |
|
|
|
|
πnx |
|
4(−1)n |
|
πnx |
|
||||||||||||
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равенство в (10) имеет место во всех точках непрерывности функ-
ции f (x) . В точках разрыва значение суммы ряда равно: |
|
|||||||||||||||||||||||||||||||||||
S(0) = |
1 |
f (0 − 0) + f (0 + 0) |
= |
|
−1 − 2 |
= − |
3 |
; |
|
|||||||||||||||||||||||||||
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
1 + 5 |
|
2 |
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
S(−3) = |
|
|
f (−3 − 0) + f (−3 + 0) |
= |
|
|
|
|
|
= 3 |
|
|
(11) |
|||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||
S(3) = |
1 |
¡f (3 − 0) + f (3 + 0) |
=¢ |
1 + 5 |
= 3 |
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x = 0. |
|
Подставляя |
||||||||
Проверим |
выполнение условия (11) в точке |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x = 0 в правую часть (10) и учитывая, что |
cos 0 = 1, |
sin 0 = 0, |
по- |
|||||||||||||||||||||||||||||||||
лучим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
∞ |
|
|
|
18 |
|
|
|
3 |
|
18 |
|
∞ |
1 |
|
|
|
|
|
|||||||||||||
S(0) = |
|
|
− |
X |
|
|
|
|
|
|
|
|
= |
|
− |
|
|
X |
|
|
|
|
|
|
|
|
= |
|
||||||||
|
4 |
k=1 |
π2(2k − 1)2 |
4 |
π2 |
|
|
|
(2x − 1)2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
3 |
|
18 |
|
|
π2 |
3 |
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
||||||||
= |
|
|
− |
|
|
|
|
· |
|
= |
|
− |
|
= − |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
π2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
8 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
10
Здесь использована известная сумма ряда (приложение 1).
Ряд Фурье (4) в общем случае можно записать в комплексной форме с комплексными коэффициентами. Воспользуемся формулами Эйлера:
πnx |
|
|
|
ei |
πnx |
+ e−i |
πnx |
|
|
|
|
|
|
|
πnx |
|
|
|
ei |
πnx |
− e−i |
πnx |
|
|||||||||||||||||||||||||
|
|
|
|
` |
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
` |
|
|
(13) |
|||||||||||||||||||||||
cos |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
sin |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a |
|
|
|
|
∞ |
|
|
|
|
ei |
πnx |
|
|
+ e−i |
πnx |
|
|
|
|
|
|
ei |
πnx |
− e−i |
πnx |
|
|||||||||||||||||||
f (x) |
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
` |
|
|
|
|
|
|
|
|
|
` |
|
` |
|
|
|
||||||||||||||||||
|
|
0 + an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ bn |
|
|
|
|
|
|
|
= |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
n=1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
|
|
|
|
∞ |
|
|
a |
n |
− ib |
|
|
|
i |
πnx |
|
|
|
a |
n |
|
+ ib |
|
|
− |
i |
πnx |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
0 |
|
|
X |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(14) |
|||||||||||||
= 2 + |
n=1 |
|
|
|
|
2 |
|
|
|
|
e |
|
|
` |
+ |
|
|
|
|
|
2 |
|
|
|
|
|
e |
|
` |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если ввести обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
C |
0 |
= |
a0 |
, C |
|
= |
an − ibn |
, C− |
n |
= |
an + ibn |
, |
|
|
|
|
(15) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ряд (14) можно переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
πnx |
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
πnx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f (x) C0 |
+ Cnei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
` |
|
|
+ C−ne−i |
|
` |
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
πnx |
|
|
|
|
−1 |
|
|
|
|
|
πnx |
|
|
|
|
|
+∞ |
|
πnx |
|
|||||||||||||||
= C |
+ |
|
|
|
|
C ei |
+ |
|
|
|
|
|
C ei |
= |
|
|
|
|
|
|
|
(16) |
||||||||||||||||||||||||||
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
C ei ` . |
||||||||||||||||||||||||||||
0 |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n=−∞ |
|
|
|
|
|
|||||||||||||
Это и есть комплексная форма ряда Фурье с комплексными коэффициентами, определяемыми по формулам (15).
Коэффициенты комплексного ряда Фурье можно получить и непосредственно, вычисляя их по формуле
`
1 |
Z |
i |
πnx |
|
|
− |
(17) |
||||
Cn = |
|
f (x)e |
|
` dx. |
|
2` |
|
|
|
|
|
−`
Непосредственное интегрирование по формуле (17) приводит к тем же выражениям для комплексных коэффициентов, что и формулы (15) (ПОЛУЧИТЬ эти коэффициенты интегрированием).
Запишем теперь в комплексной форме ряд Фурье заданной функ-
11
ции:
f (x) |
|
∞ |
|
C ei |
3 , |
|
|
где |
C |
= 3 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
X |
|
|
|
|
πnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
9 |
|
¡(−1)n − 1¢ − |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Cn = |
|
|
|
|
¡4(−1)n − 1¢, |
n = ±1, ±2, ... . |
(18) |
|||||||||||||||||||||||||||||||
2(nπ)2 |
2nπ |
|||||||||||||||||||||||||||||||||||||
1.5. Запишем частичные суммы ряда (10): |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
S0(x) = |
3 |
; |
|
|
S1(x) = |
3 |
|
− |
18 |
|
cos |
πx |
− |
5 |
sin |
πx |
; |
|
|
|
|
|||||||||||||||||
4 |
|
|
π2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
π |
3 |
|
|
|
|
|
||||||||||||
S2(x) = |
3 |
− |
18 |
cos |
πx |
− |
|
5 |
sin |
πx |
+ |
3 |
sin |
2πx |
= S1(x) + |
3 |
sin |
2πx |
||||||||||||||||||||
4 |
|
3 |
|
3 |
|
|
|
|
2π |
3 |
|
|||||||||||||||||||||||||||
|
|
|
π2 |
|
|
π |
|
|
|
2π |
3 |
|
|
|
|
|
||||||||||||||||||||||
S3(x) = S2(x) − |
2 |
|
cos πx − |
5 |
|
sin πx. |
|
|
|
|
|
|
|
|
(19) |
|||||||||||||||||||||||
π2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
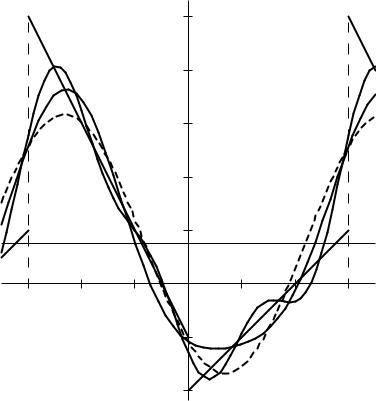
Графики частичных сумм приведены на рис. 3. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
f (x) |
5 |
6 |
|
|
|
|
|
4 |
|
|
|
S3(x) |
|
|
|
|
|
|
S2(x) |
|
|
3 |
|
|
|
S1(x) |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
S0(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
−3 −2 −1 |
|
0 |
1 |
2 |
3 x |
|
|
|
−1 |
|
|
|
|
|
|
−2 |
|
|
|
|
Рис. 3. |
Графики частичных сумм ряда Фурье |
|||||
Вывод: с ростом n графики частичных сумм Sn(x) в точках непрерывности x (−3; 0) (0; 3) приближаются к графику функ-
12
ции f (x) . В точках разрыва значения частичных сумм приближа-
ются к |
1 |
f (x − 0) + f (x + 0) . |
n |
|
|
` |
|
|
|
|
|
|
|
|||||||||||
1.6. |
|
2 |
¡ |
n |
|
|
|
` |
¢ |
|
|
|
|
|
|
|
|
|
||||||
|
Выражение |
a |
cos πnx + b |
|
sin πnx |
в ряде Фурье называется |
||||||||||||||||||
n -й гармоникой. Известно, что |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
an cos |
πnx |
+ bn sin |
πnx |
= An cos |
|
πnx |
− ϕn , |
(20) |
|||||||||||||
|
|
|
|
|
|
³ ` |
||||||||||||||||||
|
|
|
|
` |
|
|
|
` |
|
|
= |
bn |
|
|
a´n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
+ b2 , |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
An = pan |
|
bn n |
sin ϕn |
|
An |
, |
cos ϕn = An |
(21) |
|||||||||||||
или |
|
|
ϕn = arctg |
|
|
с учетом четверти. |
|
|
|
|
||||||||||||||
|
|
an |
|
|
|
|
|
|||||||||||||||||
Совокупности |
{An} |
и |
{ϕn}, |
|
|
n = 1, 2, ... , называются соответ- |
||||||||||||||||||
ственно амплитудным и фазовым спектром периодической функции. Графически спектры изображаются в виде отрезков длины An
или ϕn , проведенных перпендикулярно оси, на которую наносит- |
|
ся значение n = 1, 2, ... или ωn = πn . Спектры имеют дискретный |
|
|
` |
характер, причем расстояние между отдельными линиями спектра |
|
равно |
π для 2` -периодической функции. Графическое изображе- |
`
ние соответствующего спектра называется амплитудной или фазовой
диаграммой.
Вычислим несколько первых значений амплитудного и фазового
спектра: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
−18 |
|
|
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
||||||||||
|
|
; A1 =qa12+ b12 ≈ 2,42060; ϕ1 = arctg |
|
|||||||||||||||||||||||||||
a1 |
= |
|
|
|
|
; b1 = |
|
|
|
|
|
|
|
− π ≈ −2,4241. |
||||||||||||||||
π2 |
π |
a1 |
||||||||||||||||||||||||||||
Так как |
a1 < 0, b1 < 0, |
то ϕ1 III - четверти. |
|
|
||||||||||||||||||||||||||
a =0; |
b |
= |
3 |
; |
|
A |
= |
3 |
≈ 0,47746; |
ϕ |
= |
π |
≈ 1,5708. |
(22) |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
2π |
2 |
|
2π |
|
|
|
2 |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
−2 |
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
|
b3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
a3 |
= |
|
; b3 = |
|
; A3 =qa32+ b32 ≈ 0,56789; ϕ3 = arctg |
|
|
− π ≈ −1,9357. |
||||||||||||||||||||||
π2 |
3π |
a3 |
||||||||||||||||||||||||||||
|
Продолжим эти вычисления для |
n = 4, 5, ..., 8 |
и занесем дан- |
|||||||||||||||||||||||||||
ные в таблицу. Откладывая на графиках вертикальные отрезки соответствующей длины, получим амплитудную и фазовую диаграммы данной функции. Диаграммы приведены на рис. 4 и 5.
13

n |
|
|
an |
bn |
An |
ϕn |
||
1 |
−1,8238 |
−1,59160 |
2,42060 |
−2,4241 |
||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
0,47746 |
0,47746 |
1,5708 |
||
3 |
−0,20264 |
−0,53053 |
0,56789 |
−1,9357 |
||||
|
|
|
|
|
|
|
|
|
4 |
0 |
|
|
0,23873 |
0,23873 |
1,5708 |
||
5 |
−0,07295 |
−0,31831 |
0,32656 |
−1,7961 |
||||
|
|
|
|
|
|
|
|
|
6 |
0 |
|
|
0,15916 |
0,15916 |
1,5708 |
||
|
|
|
|
|
|
|
|
|
7 |
−0,03722 |
−0,22737 |
0,23039 |
−1,7331 |
||||
|
|
|
|
|
|
|
|
|
8 |
0 |
|
|
0,11937 |
0,11937 |
1,5708 |
||
|
|
|
|
|
|
|
|
|
|
An 6 |
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
- |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
n |
Рис. 4. Амплитудная диаграмма периодического сигнала
Вывод: с ростом n амплитудный спектр убывает (не монотонно).
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
6 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
1 |
|
2 |
|
3 |
|
4 |
|
|
|
5 |
6 |
7 |
|
8 |
|
|
|
n |
||||||||||||||||||||||||||||||||||
− |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5. Фазовая диаграмма периодического сигнала
14

Вывод: с ростом n фазовый спектр ϕ2k = π2 , ϕ2k−1 → −π2 . 1.7. Энергия периодического сигнала, длящегося от t = −∞ до
t = +∞ бесконечно велика. При рассмотрении энергетических характеристик периодического сигнала основной интерес представляет средняя мощность, которая совпадает с мощностью, средней за один период T = 2` :
|
` |
|
|
1 |
|
Ef = |
2` Z f 2(t) dt . |
(23) |
−`
Распределение этой мощности между отдельными гармониками основано на равенстве Парсеваля, справедливого для любой полной ортогональной системы базисных функций (в том числе и для системы гармонических функций). Равенство Парсеваля можно рассматривать как аналог формулы линейной алгебры, в которой квадрат нормы вектора равен сумме квадратов координат:
|
1 |
|
|
` |
|
|
|
|
|
|
|
a2 |
|
∞ |
|
|
|
||
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
a2 |
1 |
|
|
|
|
X ¡ |
¢ |
|
|||||||
|
|
|
|
|
` |
|
∞ |
|
|
||||||||||
|
|
|
|
|
f |
2 |
(x) dx = |
0 |
|
+ |
|
an2 + bn2 |
, |
(24) |
|||||
|
` |
|
|
|
|
|
|
|
|
|
2 |
|
|
n=1 |
|
|
|
||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
|
0 |
+ |
|
|
X ¡ |
a2 |
+ b2 |
¢ |
|
(25) |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
E = |
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
f |
|
|
|
4 |
|
2 n=1 |
n |
n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, смысл равенства Парсеваля состоит в следующем: полная средняя мощность периодического сигнала равна сумме средних мощностей, выделяемых отдельными гармониками.
С физической точки зрения равенство Парсеваля означает, что для того, чтобы найти c заданной точностью приближенное значе-
ние средней мощности, достаточно сложить квадраты амплитуд нескольких первых гармоник. Так как амплитудный спектр убывает, гармоники с достаточно большими номерами не будут вносить существенного вклада в среднюю мощность.
Проверим выполнение равенства Парсеваля для заданной функции (3). Вычислим интеграл в левой части (24):
3 |
|
3 |
f 2(x) dx = 3 |
" |
|
0 |
3 |
(26) |
|
|
|
(−2x − 1)2dx + |
(x − 2)2dx# = 8. |
||||
1 |
Z |
1 |
|
Z |
Z |
|
||
− |
3 |
|
|
− |
3 |
0 |
|
|
Вычислим правую часть равенства (24). Для этого подсчитаем
15
квадраты коэффициентов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
a02 |
|
= 9 |
= 1,125, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(27) |
|||||
|
|
a2 |
= 162 |
|
|
|
1 |
|
1 − (−1)n , |
|
|
b2 |
|
|
|
|
1 |
|
|
17 − 8(−1)n . |
|||||||||||||||||||||||||||||||||||
|
|
· |
|
|
|
= |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
π4 |
|
|
|
n4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
π2n2 |
¡ |
|
|
|
|
|
|
|
|
¢ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
части (24): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Найдем сумму ряда¡в правой ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
∞ |
|
|
|
162 |
|
1 |
|
|
|
|
|
162 (−1)n+1 |
17 |
|
|
|
1 |
|
|
|
|
|
8 |
|
|
|
|
1)n+1 |
|
|
|
||||||||||||||||||||||||
n=1 ³ |
|
+ |
|
· |
|
+ |
|
|
|
|
|
|
´ = |
|
|||||||||||||||||||||||||||||||||||||||||
π4 · |
n4 |
|
π4 |
· |
|
|
|
|
n4 |
|
|
|
+ π2 |
n2 |
|
|
π2 |
· (−n2 |
|
|
|
||||||||||||||||||||||||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= 162 |
∞ |
1 |
+ |
|
162 |
∞ |
|
(−1) |
n+1 |
|
|
|
∞ |
1 |
|
|
+ |
8 |
∞ |
|
|
|
n+1 |
= (28) |
|||||||||||||||||||||||||||||||
X |
|
X |
|
|
|
+ 17 |
X |
|
|
X |
(−1) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
π4 |
n=1 |
n4 |
|
|
|
|
|
π4 |
n=1 |
|
|
|
n4 |
|
|
|
π2 |
n=1 |
|
n2 |
|
|
|
π2 |
n=1 |
|
n2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
162 |
· |
π4 |
|
162 |
· |
7π4 |
|
|
|
17 |
· |
π2 |
|
|
8 |
|
· |
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= |
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
= 6,875 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
π4 |
90 |
|
|
π4 |
720 |
π2 |
6 |
π2 |
12 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Здесь использованы известные суммы некоторых рядов. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
X ¡ |
an2 + bn2 |
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(29) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
= 1,125 + 6,875 = 8. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для ряда (10) равенство Парсеваля выполняется. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Согласно (25) и (26), средняя мощность сигнала |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(30) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ef = 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Запишем математический смысл равенства Парсеваля. Отметим, что тригонометрический ряд Фурье обладает важным
свойством: при фиксированном числе слагаемых ряда N он обеспе-
чивает наилучшую аппроксимацию в смысле минимума среднеквадратической ошибки, т.е. среднеквадратическая ошибка
M = v |
|
|
|
|
|
|
|
|
|
3 |
f (x) − N |
an cos |
πnx |
+ bn sin |
πnx |
2dx (31) |
|||
|
3 |
|
3 |
||||||
u Z µ |
|
|
|
|
¶ |
|
|||
u |
3 |
X |
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
− |
n=0 |
|
достигает минимума, когда коэффициенты ряда вычисляются по формулам (5), (6).
С математической точки зрения выполнение равенства Парсеваля означает, что ряд Фурье сходится в среднем к функции f (x), т.е. что среднеквадратическая ошибка стремится к нулю и выполняется соотношение
|
3 |
|
N |
|
|
|
|
Z µ |
|
|
πnx |
¶ |
|||
|
|
|
X |
πnx 2 |
|||
|
3 |
|
|
|
|
dx = 0. (32) |
|
lim |
|
f (x) − |
an cos |
3 |
+ bn sin |
3 |
|
N →∞ |
|
|
n=0 |
|
|
||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16
Из этого, однако, еще не следует, что ряд Фурье сходится к функции f (x) равномерно, т.е. что при достаточно больших N при всех значениях x из отрезка [−3; 3] модуль разности можно сделать сколь угодно малым:
|
|
N |
3 |
+ bn sin |
3 |
¯ |
< ε. |
(33) |
|
¯f (x) − n=0 an cos |
|||||||
|
¯ |
X |
πnx |
|
πnx |
¯ |
|
|
В |
¯ |
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
¯ |
|
|
некоторых точках оси Ox эта разность может быть и велика, важно только, чтобы интеграл от ее квадрата по отрезку [−3; 3] был мал для больших N.
Итак, из сходимости в среднем ряда Фурье к функции f (x) , для которой он составлен, еще не следует, что суммой этого ряда является f (x). В то же время, ряд Фурье, составленный для функции, непрерывной и кусочно-гладкой на всей числовой оси, сходится к этой функции равномерно. Такой ряд можно почленно дифференцировать, интегрировать, и его сумма равна функции.
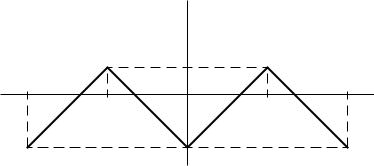
1.8. Продолжим функцию y1 = x−2, x [0; 3) периодически на всю числовую ось четным образом. Получим периодическую функцию f1(x) с периодом T = 2` = 6 , график которой приведен на рис. 6. Так как полученная периодическая функция f1(x) непрерывна на всей числовой оси, ряд Фурье сходится равномерно к f1(x) , и график суммы ряда S(x) полностью совпадает с графиком f1(x) .
|
6 |
(x) |
|
|
S(x) f1 |
|
|
|
1 |
|
|
−6 |
|
|
6 - |
−3 |
0 |
3 |
x |
|
−2 |
|
|
Рис. 6. График четной периодической функции и суммы ряда Фурье
Вычислим коэффициенты ряда Фурье этой четной функции. Все
коэффициенты bn = 0 в силу нечетности подынтегральных функций
πnx` .
17
|
` |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a0 = |
2 |
Z f1 |
(x) dx = |
2 |
|
Z (x − 2) dx = −1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
` |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
` |
|
πnx |
2 |
|
3 |
|
|
πnx |
6 |
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
an = |
|
Z f1 |
(x) cos |
|
|
|
|
dx = |
|
|
Z (x−2) cos |
|
|
dx = |
|
|
|
(cos πn−1) = |
|||||||||||
` |
` |
|
|
|
3 |
|
3 |
(πn)2 |
|||||||||||||||||||||
|
0 |
|
(−1)n − 1 = |
( |
|
|
0 |
2 |
|
, n = 2k − 1 . |
|
|
(34) |
||||||||||||||||
= (πn)2 |
|
|
|
2 −12 |
|
|
|
||||||||||||||||||||||
|
6 |
|
¡ |
|
¢ |
|
|
|
|
0 |
|
|
, n = 2k |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
π (2k − 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Действительная форма ряда Фурье четной функции имеет вид |
|
||||||||||||||||||||||||||||
|
|
|
|
f (x) −1 + |
∞ |
|
−12 |
|
|
|
|
cos π(2k − 1) x . |
(35) |
||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
k=1 |
|
π2(2k − 1)2 |
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ряд Фурье четной функции содержит только косинусоидальные гармоники.
Для проверки вычисления подставим в левую и правую части выражения (35) значение x = 0: f1(0) = −2;
|
|
|
|
1 |
|
∞ |
|
|
|
−12 |
|
|
|
|
1 |
|
12 π2 |
1 |
|
3 |
|
|
||||||||||||
|
|
|
|
|
X |
|
|
|
|
|
|
|
(36) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
· |
|
|
|
|
|
|
|
|
||||||||
|
S(0) = − |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
= − |
|
− |
|
|
= −2. |
||||||||
|
2 |
|
π2 |
(2k − 1)2 |
|
|
π2 |
|
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
8 |
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Получили верное равенство: |
f1 |
(0) = S(0) . В остальных точках |
|||||||||||||||||||||||||||||||
равенство |
|
f1 |
(x) = S(x) |
также выполняется. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Запишем комплексную форму ряда Фурье. Для четной функции |
|||||||||||||||||||||||||||||||||
f1 |
(x) |
все |
bn = 0, следовательно, все коэффициенты комплексного |
|||||||||||||||||||||||||||||||
ряда Фурье действительные числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
C |
= |
−1 |
; |
|
C |
n |
= |
an |
= |
3 |
|
|
|
(−1)n − 1 , n = ± 1, ±2, . . . . |
(37) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
0 |
2 |
|
|
|
|
2 |
|
|
(πn)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фурье четной функции f (x) имеет вид |
||||||||||||||||||
|
Комплексная форма ряда |
|
|
|
|
¡ |
|
|
|
|
¢ |
|
|
|
|
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
πnx |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
f1(x) |
|
|
X Cnei |
3 . |
|
|
|
|
|
|
(38) |
|||||||||||
n=−∞
Для четной функции принято считать ϕn = 0 (так как bn = 0 ) и рассматривать амплитудный спектр коэффициентов an, которые откладываются на диаграмме с соответствующим знаком (рис. 7).
Вывод: амплитудный спектр убывает по модулю (не монотонно). В этом случае говорят, что огибающая огибающих амплитудного спектра стремится к нулю.
18

an 6 |
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
- |
|
|
|
|
−0.0486 −0.0248 |
n |
||||
|
|
|
−0.135 |
|
|
|
|
|
|
−0.5 |
|
|
|
|
|
|
|
|
|
−1


 −1.216
−1.216
Рис. 7. График амплитудного спектра четной периодической функции
1.9. Продолжим функцию |
y1 = x − 2; x [0, 3) периодически |
на всю числовую ось нечетным образом. Получим периодическую |
|
функцию f2(x) с периодом |
T = 2` = 6, график которой приве- |
ден на рис. 8. Нечетная периодическая функция f2(x) удовлетворяет условиям Дирихле, следовательно, для нее можно записать ряд Фурье. Вычислим коэффициенты этого ряда:
|
3 |
|
πnx |
|
−2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||
bn = |
3 Z |
(x − 2) sin |
3 |
dx = |
πn |
¡ |
2 + (−1)n . |
(39) |
|
|
0 |
|
|
|
|
|
¢ |
|
|
|
|
f2(x) 6 |
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
µ 1 |
|
|
|
µ |
|
|
−6 |
µ |
|
|
µ |
|
|
- |
|
|
|
|
−3 |
0 |
|
3 |
|
6 |
x |
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
Рис. 8. |
График нечетной периодической функции |
|
|||||||
Коэффициенты a0 = 0, an = 0 в силу нечетности подынтегральных функций f2(x) cos πnx` . Действительная форма ряда Фурье
19
нечетной функции имеет вид |
|
sin πnx . |
|
||||
f (x) |
∞ |
−2 |
2 + (−1)n |
(40) |
|||
2 |
X |
|
¡ |
¢ |
|
|
|
n=1 |
πn |
|
3 |
|
|
||
|
|
|
|
||||
Ряд Фурье нечетной функции содержит только синусоидальные гармоники.
Для проверки вычислений подставим в левую и правую части
|
|
|
|
|
|
|
|
|
x = 3 |
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
выражения (40) значение |
∞ |
2 |
: |
|
f2 |
³ 2 ´ = − |
2 |
; |
|
|
|
||||||||||||||||||
|
|
3 |
´ = n=1 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
πn |
|
|
|||||||||||
|
|
S³ |
|
|
|
|
|
2 + (−1)n |
|
sin |
|
|
|
|
. |
(41) |
|||||||||||||
|
|
2 |
πn |
|
|
2 |
|||||||||||||||||||||||
Учитывая, что |
|
|
X |
|
|
|
¡ |
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
πn |
= ½ |
|
|
|
0 |
|
|
, n = 2k |
|
|
|
|
|
|
|
(42) |
||||||||||
|
|
sin |
|
|
(−1)k+1 , n = 2k − 1, |
|
|||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||
выражение (41) перепишется в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
∞ |
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S³ 2 |
´ = k=1 π(2k − 1) 2 + (−1)2k−1 ·(−1)k+1 = |
|
|||||||||||||||||||||||||||
|
|
X |
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= − |
|
|
2(−1)k+1 |
= |
|
−2 |
· |
π |
|
= − |
1 |
|
|
(43) |
|||||||||||||
|
|
|
π(2k − 1) |
|
4 |
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
3 = S |
3 . |
|
|
|
|||||||||||||
Получили верное равенство: f |
2 |
|
Здесь использова- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
на известная сумма ряда. В остальных точках непрерывности функ- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
³ ´ |
|
³ ´ |
|
|
|
|
ции равенство |
f2 |
(x) = S(x) |
также выполняется. |
|
|
|||||||||||
Для нечетной функции все |
an = 0, |
|
следовательно, коэффици- |
|||||||||||||
енты комплексного ряда Фурье чисто мнимые числа: |
|
|||||||||||||||
C = 0; C |
n |
= −i |
bn |
= |
|
i |
|
2 + (−1)n |
|
, n = ± 1, ±2, . . . . |
(44) |
|||||
|
|
|
|
|
|
|||||||||||
0 |
|
|
2 πn |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Комплексная форма ряда Фурье нечетной функции f (x) |
имеет |
|||||||||||||||
вид |
|
|
|
|
|
|
|
|
¡ |
|
¢ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
πnx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cnei |
|
|
|
(45) |
||
|
|
|
|
f (x) |
|
3 . |
|
|
|
|||||||
|
|
|
2 |
|
|
|
n=−∞ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
π (так как a = 0 ) |
|
Для нечетной функции принято считать ϕ |
n |
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
n |
|
и рассматривать амплитудный спектр коэффициентов bn, которые
откладываются на диаграмме с соответствующим знаком (рис. 9). Вывод: амплитудный спектр убывает по модулю (не монотон-
но). В этом случае говорят, что огибающая огибающих амплитудного спектра стремится к нулю.
20
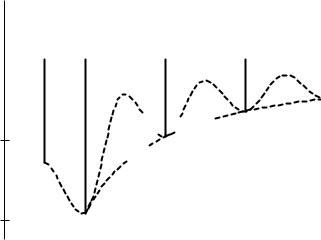
bn 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−0.239
−0.5








 −0.318
−0.318 

 −0.477
−0.477
−1 −0.955
Рис. 9. График амплитудного спектра нечетной периодической функции
1.10. Из формул (10), (35) и (40), дающих разложение в ряд Фурье на отрезке [0; 3] одной и той же функции y = x − 2, x [0; 3), можно сделать следующий вывод:
вид ряда Фурье зависит от того, как была периодически продолжена функция на всю числовую ось. При четном продолжении ряд содержит только косинусы, при нечетном синусы, произвольное продолжение содержит оба вида гармоник. Все три ряда, имея различные коэффициенты, в точках x (0; 3) сходятся к одним и тем же значениям. Однако четное продолжение более предпочтительно, т.к. ряд Фурье в этом случае сходится равномерно.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ. НЕПЕРИОДИЧЕСКАЯ ФУНКЦИЯ (ЧАСТЬ 2)
2.1. Пусть задан прямоугольный импульс |
(46) |
||
g1(t) = ½ |
0, |
t (−6; −3) (3; 6) . |
|
|
3, |
t [−3; 3] |
|
Для сравнения спектральных характеристик периодического и непериодического сигналов продолжим сначала этот импульс периодически на все числовую ось с периодом T = 2` = 12 и построим график полученной периодической функции g2(t) (рис. 10). Периодическая функция g2(t) удовлетворяет условиям Дирихле и может быть разложена в ряд Фурье. Функция g2(t) четная, следователь-
21
но, bn = 0 и все коэффициенты комплексного ряда Фурье являются действительными числами:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn = |
an |
. |
|
|
|
|
|
|
|
(47) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
Вычислим эти коэффициенты. Из формул (5) и (15) имеем: |
|||||||||||||||||||||||||||||
C |
= a0 |
= 1 · |
1 |
|
|
|
6 |
g (t) dt = 1 |
|
3 |
|
|
|
|
(48) |
||||||||||||||
|
Z |
|
3 dt = 3 ; |
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
||||
2 |
|
2 |
|
|
6 |
|
|
6 |
12 |
|
3 |
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||
|
|
an |
1 |
|
1 |
|
|
6 |
|
|
|
πnt |
|
|
3 |
|
|
|
πn |
||||||||||
Cn |
= |
|
|
= |
|
|
· |
|
|
|
Z |
g2 |
(t) cos |
|
|
|
|
dt = |
|
sin |
|
= |
|||||||
|
|
|
6 |
|
|
|
|
|
|
2 |
|||||||||||||||||||
|
2 |
|
2 |
|
|
|
6 |
|
6 |
|
|
|
πn |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
, n = 2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3(−1)k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
π(2k − 1) , n = 2k − 1, |
k = ± 1, ±2, . . . . |
|
||||||||||||||||||
|
|
в комплексной форме имеет вид |
|
|
|
|
|
|
|
||||||||||||||
Ряд Фурье |
|
|
−1 |
3(−1) |
k+1 |
|
|
π(2k−1)t |
|
|
3 + |
|
|
||||||||||
|
|
g2(t) |
X |
|
· ei |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
6 + |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=−∞ |
π(2k − 1) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
3(−1)k+1 |
|
i π(2k−1)t |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||
|
|
|
|
|
+ |
π(2k − 1) · e |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
6g2(t) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
−9 −6 |
|
−3 |
|
|
0 |
|
|
3 |
6 |
|
9 |
t |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10. |
График четного периодического импульса |
|||||||||||||||||||||
(49)
(50)
Спектральная диаграмма действительных коэффициентов Cn, вычисленных по формулам (48) и (49), приведена на рис. 11. Для четной функции фазовый спектр ϕn = 0, коэффициенты Cn, n = 0, ±1, ±2, . . . откладываются на диаграмме со знаком в виде вертикальных отрезков соответствующей длины. Пунктирной линией показана огибающая дискретного спектра.
22
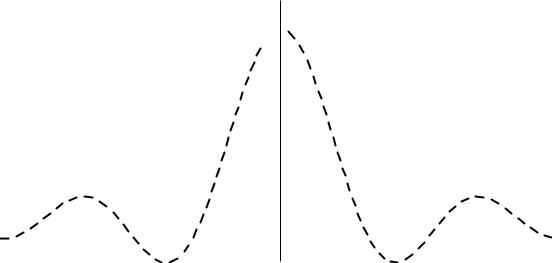
C0 = 32 
 6Cn
6Cn
−π |
|
− |
2π |
− |
π |
|
|
|
|
|
|
|
π |
|
ωn= |
π ·n |
||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
6 - |
||
− |
5π |
|
|
|
|
− |
π |
− |
π |
0 π |
π |
|
2π 5π π |
|
||||
|
6 |
|
|
|
|
|
3 |
|
|
6 |
6 |
3 |
|
3 |
6 |
|
||
Рис. 11. Спектральная диаграмма коэффициентов Cn четного периодического сигнала
2.2. Рассмотрим прямоугольный видеоимпульс
g(t) = ½ |
0, t / [−3; |
3]. |
(51) |
|
3, t [−3; |
3] |
|
Эта четная функция не является периодической. Информацию о спектральных характеристиках непериодической функции несет непрерывная комплекснозначная функция спектральная плотность, определяемая с помощью прямого преобразования Фурье
|
+∞ |
|
|
F (ω) = |
Z |
g(t) · e−iωtdt. |
(52) |
−∞
Спектральную плотность можно рассматривать как математическую модель сигнала в частотной области. Один и тот же сигнал допускает две равноправные математические модели: функцию g(t) во временной области и функцию спектральной плотности в области частот [2].
Условием существования спектральной плотности является абсолютная интегрируемость сигнала:
+∞
Z
¯g(t)¯ dt < ∞. |
(53) |
|
¯ |
¯ |
|
−∞
Кроме того, функция g(t) должна иметь конечное число экс-
23

тремумов, а также конечное число точек разрыва первого рода на любом конечном интервале. Очевидно, функция (41) удовлетворяет всем этим условиям.
Найдем ее спектральную плотность:
|
+∞ |
|
|
|
3 |
|
|
|
|
3 |
|
3 |
|
|
Z |
|
|
Z |
|
|
|
|
|
¯ |
|
|
|
F (ω) = g(t) · e−iωtdt = |
|
3 |
|
|
|
|
|
−3 |
= |
||||
|
3 · e−iωtdt = −iω e−iωt |
¯ |
|||||||||||
3 · 2 |
|
e3iω − e−3iω |
|
|
|
sin 3ω |
|
¯ |
|
|
|||
−∞ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
= |
|
· |
|
= 6 |
|
|
|
= 18 sinc(3ω). |
|
|
(54) |
||
ω |
2i |
ω |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Здесь использована функция |
|
|
|
|
|
|
|
|
|
||||
|
|
|
sinc(x) = |
sin(x) |
. |
|
|
|
(55) |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|
|
|
|
||
В силу того, что импульс (51) является четной функцией, его
спектральная плотность (54) оказалось действительной функцией. График спектральной плотности приведен на рис. 12.
18 6F (ω)
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
- |
−π − |
2π |
− |
π |
0 |
π |
2π |
π |
|
3 |
|
3 |
|
3 |
3 |
|
Рис. 12. График спектральной плотности четного импульса
Сравнивая рис. 11 и 12, можно сделать вывод: огибающая дискретного спектра периодического импульса совпадает по форме с графиком спектральной плотности аналогичного непериодического сигнала. По оси частот не происходит изменения масштаба, а амплитуда спектральной плотности увеличивается в 2` раз, где ` = 6. Теоретическое подтверждение этого факта следует из формул (17) и (52).
24
В общем случае спектральная плотность F (ω) является комплекснозначной функцией. Модуль этой функции
|
¯ |
¯ |
q |
¡ |
¢ |
¡ |
¢ |
|
|
(56) |
S(ω) = |
¯ |
F (ω) |
= |
|
Re F (ω) 2 |
+ |
Im F (ω) |
2 |
|
|
|
¯Θ(ω) = arg F (ω) |
|
|
|
|
(57) |
||||
называется амплитудным |
спектром сигнала [1], а аргумент |
|
||||||||
называется фазовым спектром сигнала [1]. Для четного сигнала |
||||||||||
S(ω) = F (ω), |
Θ(ω) = arctg 0 + πk = πk . |
(58) |
||||||||
2.3. Рассмотрим спектральную плотность импульса g2(t), получен- |
|||
ную из (51) увеличением амплитуды в |a| = 2 раза: |
(59) |
||
g2(t) = ½ |
0, |
t / [−3; 3]. |
|
|
6, |
t [−3; 3] |
|
Для краткости записи введем обозначение: соответствие сигнала
и спектральной плотности будем записывать как f (t) ↔ F (ω). |
|
Воспользуемся свойством линейности спектральной плотности: |
|
если f (t) ↔ F (ω), то a · f (t) ↔ a · F (ω) a = const. |
(60) |
Таким образом, спектральная плотность сигнала g2(t) равна |
(61) |
S2(ω) = 36 sinc 3ω . |
Вывод: при увеличении амплитуды импульса в a раз, амплитудный спектр сигнала увеличивается во столько же раз, а фазовый спектр сигнала не изменяется.
2.4. Рассмотрим спектральную плотность импульса |
g3(t), получен- |
|||||||||||
ного из g2(t) увеличением длительности в |b| = 4 |
раза: |
|
||||||||||
|
|
|
6, |
t [−12; 12] |
|
|
|
|
||||
|
g3(t) = ½ 0, |
t / [−12; 12]. |
|
|
|
(62) |
||||||
Воспользуемся свойством изменения масштаба времени: |
|
|||||||||||
|
f (t) ↔ F (ω), то f (α · t) ↔ |
1 |
|
ω |
|
|
|
|||||
если |
α F ³ |
α ´ |
α > 0. |
(63) |
||||||||
|
t |
|
1 |
|
||||||||
Так как g3(t) = g2 |
|
, α = |
4 , |
то, согласно (63), спектральная |
||||||||
4 |
||||||||||||
плотность более длительного импульса будет равна |
|
|
||||||||||
|
³ |
|
´ |
|
|
|
|
|
|
|
(64) |
|
|
F3(ω) = 4F2(4ω) = 144 sinc(12ω) . |
|
||||||||||
Вывод: при увеличении длительности импульса в |b| раз амплитуда спектральной плотности увеличивается во столько же раз, и во столько же раз график спектральной плотности сжимается по оси частот. При уменьшении длительности импульса в |b| раз амплитуда спектральной плотности уменьшается во столько же раз, и во столько же раз график спектральной плотности растягивается по оси частот.
25

В радиотехнике это свойство называется зависимостью меж-
ду длительностью сигнала и шириной спектра и имеет первостепенное значение. Так, чем меньше длительность импульса, тем шире его спектр, поэтому короткие импульсные помехи, имеющие широкий спектр, могут ухудшить условия радиоприема в значительном диапазоне частот [2].
2.5. Рассмотрим сигнал g4(t), полученный из g3(t) сдвигом на |с|=1 сек по оси времени (рис. 13).
6g4(t)
6
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
−11 |
0 1 |
13 |
|
t |
||
Рис. 13. График импульса, сдвинутого по оси времени
Для определения спектральной плотности воспользуемся свойством сдвига сигнала во времени:
если f (t) ↔ F (ω), то |
f (t − t0) ↔ e−iωt0 F (ω) |
(65) |
|||||||
f (t + t0) ↔ eiωt0 F (ω) . |
|||||||||
Так как g4(t) = g3(t−1), |
то новая спектральная плотность будет |
||||||||
равна |
|
(ω) = e−iω F (ω) = e−iω 144 sinc(12ω) . |
|
||||||
F |
(66) |
||||||||
|
4 |
|
|
|
3 |
|
|
|
|
Функция (66) является уже комплекснозначной. Однако |
|
||||||||
следовательно, |
|
|
¯ |
F4 |
(ω) |
= |
¯ |
F3(ω) , |
(67) |
|
|
|
¯ |
|
¯ |
|
|||
|
амплитудный спектр сигнала не зависит от поло- |
||||||||
жения сигнала на оси |
времени. Фазовый спектр сигнала изменяет- |
||||||||
¯ |
|
¯ |
|
¯ |
¯ |
|
|||
ся на величину |
−ωt0 = −ω : |
|
|
|
(68) |
||||
|
|
Θ4(ω) = Θ3(ω) − ωt0 = −ω . |
|||||||
Справедливо и обратное утверждение: если составляющим спектра дать фазовый сдвиг на ±t0, то сигнал сдвигается во времени на ±t0.
26

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ. ПРОИЗВОЛЬНАЯ НЕПЕРИОДИЧЕСКАЯ ФУНКЦИЯ (ЧАСТЬ 3)
Найдем спектральную плотность сигнала |
(69) |
|||
q(t) = |
½ t · |
0 , |
t < 0 |
|
|
|
e−t , |
t > 0 |
|
График этой функции приведен на рис. 14.
|
|
q(t) 6 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
- |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
t |
|
Рис. 14. |
График непериодической функции |
|
||||
Функция q(t) является абсолютно интегрируемой:
+∞ |
+∞ |
(70) |
|
Z |
q(t) dt = Z |
t · e−tdt = 1 |
|
¯ |
¯ |
|
|
¯ |
¯ |
|
|
−∞ 0
и имеет только один максимум в точке t = 1. Следовательно, спектральная плотность функции q(t) существует и определяется по формуле
|
+∞ |
|
|
|
|
|
+∞ |
|
|
|
|
−1 |
|
|
|
|
|
+∞ |
|
|
||
|
Z |
q(t) e−iωtdt = |
Z |
|
|
|
|
|
|
|
|
|
¯ |
|
|
+ |
||||||
Q(ω) = |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||
t e−te−iωtdt = 1 + iω t e−t(1+iω) |
¯ |
|
||||||||||||||||||||
−∞ |
|
+∞ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|||||
|
|
1 |
|
Z |
e−t(1+ iω)dt = |
−1 |
e−t(1+iω) |
¯ |
+∞ |
|
1 |
|
|
|
||||||||
+ |
|
|
|
|
= |
|
|
= |
||||||||||||||
1+ iω |
(1+ iω)2 |
0 |
(1+ iω)2 |
|||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
= |
|
1 |
|
|
= |
|
(1−ω2)−2iω |
|
1−ω2 |
¯ |
|
2iω |
|
|
|
(71) |
||||||
|
|
|
|
|
|
|
|
|
= |
|
|
− |
|
|
|
. |
||||||
|
2 |
|
|
|
|
2 2 |
|
2 |
2 2 |
2 |
|
2 |
||||||||||
(1−ω |
)+2iω (1−ω ) + 4ω |
|
|
|
(1+ ω ) |
|
|
(1+ ω |
) |
|
|
|
||||||||||
Функция Q(ω) |
является комплекснозначной. Модуль спектраль- |
|||||||||||||||||||||
27

ной плотности (амплитудный спектр сигнала) |
|
|
|
|
|
|
|||||||
S(ω) = Q(ω) = |
|
Re Q 2+ Im Q |
2 = q |
1−ω |
2 2+ 4 ω2 |
= |
1 2 . |
(72) |
|||||
|
ω |
2 |
) |
2 |
|||||||||
|
|
q |
|
|
¡ |
|
|
|
|
1+ ω |
|
||
|
|
|
|
(1 + ¢ |
|
|
|
|
|
|
|||
График амплитудного спектра |
¢сигнала (69) приведен на рис. 15. |
||||||||||||
¯ |
¯ |
¡ |
¢ |
¡ |
|||||||||
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
−3 |
−2 |
−1 |
0 |
|
1 |
|
|
|
2 |
|
3 ω |
|
|
Рис. 15. График модуля спектральной плотности сигнала |
|
||||||||||||
Найдем фазовый спектр сигнала (66). Он равен аргументу спек- |
|||||||||||||
тральной плотности (рис. 16): |
|
|
|
|
|
|
|
|
|
||||
|
Θ(ω) = arg Q(ω) = arctg Im Q |
= arctg |
2ω |
|
. |
(73) |
|||||||
|
|
|
|
|
Re Q |
|
|
|
|
ω2 − 1 |
|
|
|
Проверим выполнение равенства Парсеваля для непериодическо- |
|||||||||||||
го сигнала |
q(t) |
[4]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
1 |
|
|
Z |
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Eq = |
|
|
q2(t) dt = |
2π |
|
|
|
|
|
Q(ω) 2dω . |
|
|
|
|
|
(74) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Вычислим интеграл в левой части |
этого равенства: |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
+∞ |
+∞ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
∞ |
|
1 |
|
|
|||||||
−∞q2 |
(t) dt = t2e−2t |
dt = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. (75) |
||||||||||||||||||
2 t2e−2t |
− 2 t e−2t − |
4 e−2t |
¯0 |
4 |
|
|||||||||||||||||||||||||||||||||
|
Z |
|
|
Z |
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´¯ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
+∞ |
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|||
|
|
Вычислим интеграл в |
правой части равенства |
Парсеваля: |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|Q(ω)|2dω = 1 |
|
|
|
|
|
|
¯ |
|
|
|
|
|
||||||||||||||||||||||
1 |
|
|
|
|
|
dω |
= |
1 |
|
|
|
|
|
|
ω |
|
+ 1 arctg ω |
|
|
|
= |
|||||||||||||||||
|
|
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
|
´¯ |
+∞ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
||
2π |
|
2π (1+ ω2) |
|
2π 2(1+ ω2) |
|
|
2 |
|
|
|
¯ |
−∞ |
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
π |
|
|
π |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
−∞ |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
= |
|
³0 + |
|
+ |
|
´ = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(76) |
||||||||||||
|
|
|
|
2π |
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
28
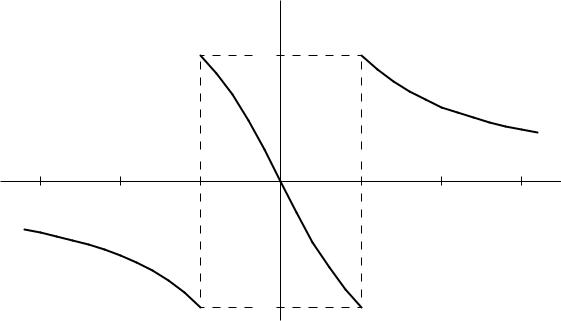
|
|
|
π 6Θ(ω) |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
- |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 ω |
|
|
− |
π |
|
|
|
|
|
|
2 |
|
|
|
|
Рис. 16. |
График фазового спектра сигнала |
|
|||
Итак, равенство Парсеваля выполняется. Так как левая часть этого равенства есть полная энергия сигнала, из (74) следует, что
полная энергия непериодического сигнала равна сумме энергий всех его спектральных составляющих. В этом состоит энергетический смысл равенства Парсеваля. Величина |Q(ω)|2 имеет смысл энергии, приходящейся на 1 Гц, и может рассматриваться как энергетический спектр сигнала. Важно отметить, что энергия непериодического сигнала, как и периодического, не зависит от фазировки спектральных составляющих [1].
Отметим существенное отличие между равенствами Парсеваля для периодического (26), и непериодического (74) сигналов. В (26) речь идет о средней мощности, получаемой делением энергии за один период на длину периода. Для непериодического сигнала такое усреднение на бесконечном интервале дает нулевую среднюю мощность. Поэтому в случае непериодического сигнала можно говорить лишь о средней мощности на конечном интервале и смысл равенства Парсеваля полная энергия сигнала [1].
29
