ЦОС учебник

R- < z < R+ ,

то можно вычислить реализуемую часть, разложив его на простые дроби. Действительно, в общем случае (см. формулу (6.34)):

полюсы кратности Nl . Реализуемая часть получится, если взять из этого разложения только те слагаемые, которые соответствуют последовательностям, отличным от нуля при n ³ 0 :

– то есть часть дельта-импульсов и правосторонние экспоненты. Итак, возвращаясь к задаче восстановления, если наблюдаемый

На практике, как уже говорилось, наблюдаемый сигнал g (n) не

является белым шумом. Но мы можем превратить его в таковой, пропустив через специально рассчитанную ЛИС-систему – “ отбеливающий” фильтр. При этом вся процедура восстановления приобретает вид, показанный на Рисунке 6.7, то есть будет представлять собой последовательное соединение отбеливающего и восстанавливающего фильтров.

153

Рисунок 6.7 - Физически-реализуемый оптимальный восстанавливающий фильтр

Hвосст ( z )

Пусть Hотб ( z ) – передаточная функция отбеливающего фильтра, а w(n) – последовательность на его выходе. Тогда:

Выразим входящие в (14.58) z-преобразования через известные нам характеристики. Во-первых, определим передаточную функцию отбеливающего фильтра. По смыслу его применения, должно быть:

Φw ( z ) = Hотб ( z ) Hотб (z−1 )Φg ( z ) = 1

или

Здесь необходимо решить задачу факторизации функции Φ g ( z )

где Φ+g ( z ) – передаточная функция физически реализуемой ЛИС –

системы, имеющая нули расположенные внутри единичной окружности. Последнее требование обусловлено тем, что из (6.60) и (6.61) мы получаем:

и упомянутые нули (ставшие теперь полюсами) обеспечат устойчивость отбеливающего фильтра.

154

Рисунок 6.8 - Структурная схема ЛИС – системы, реализующей рекуррентное восстановление сигнала

6.6 Восстановление сигнала КИХ-фильтром

Построим теперь субоптимальный восстанавливающий КИХ-

взвешенная сумма конечного числа отсчетов наблюдаемого сигнала g (n) , то есть здесь оценка строится нерекурсивно, как результат непосредственного вычисления свертки

k D

где D – конечное множество отсчетов, задающее “ окно” обработки. Выбрав область D вокруг восстанавливаемого отсчета

достаточно большого размера и рассчитав оптимальные коэффициенты КИХ-фильтра, можно получить среднеквадратичную погрешность восстановления, очень близкую к минимально достижимой, обеспечиваемой оптимальным физически нереализуемым линейным фильтром. Более того, даже при относительно небольших размерах окна обработки ошибка получается, как правило, меньше, чем у физически реализуемого восстанавливающего БИХ-фильтра. Это происходит благодаря тому, что в данном случае формируется “ двусторонняя” (интерполяционная) оценка, в которой учтены не только “ прошлые”, но и некоторое число “ будущих” отсчетов наблюдаемого сигнала.

158

Естественно, в этом случае восстановление реализуется с некоторой задержкой.

Задача синтеза субоптимального восстанавливающего КИХ- фильтра заключается в определении значений hвосст (n) в пределах

окна обработки, обеспечивающих минимум среднеквадратичной ошибки восстановления. Как и ранее, они определяются из системы уравнений (6.12). Отличие от предыдущих случаев состоит в том, что теперь область D содержит конечное число элементов – ND . Поэтому уравнение Винера-Хопфа (первая строка системы (6.12)) определяет систему из ND линейных алгебраических уравнений с таким же числом неизвестных – значений искомой импульсной характеристики. Методы решений таких систем хорошо известны.

Пример 6.4. Построим простейший КИХ-фильтр вида (6.71) – процедуру восстановления сигнала по трем точкам:

1

( ) = ∑ ( ) ( − ) =

f n hвосст k g n k

k=−1

=hвосст (−1) g (n + 1) + hвосст (0) g (n) + hвосст (1) g (n −1)

для экспоненциально коррелированного сигнала, искаженного статически независимым белым шумом (для модели наблюдения (6.26)). Здесь D = { −1, 0, 1} . Из уравнения Винера-Хопфа получаем:

B fg (−m) = B f (−m) = B f (m) = σ2f ρ m ,

поэтому записанная система уравнений конкретизируется:

159

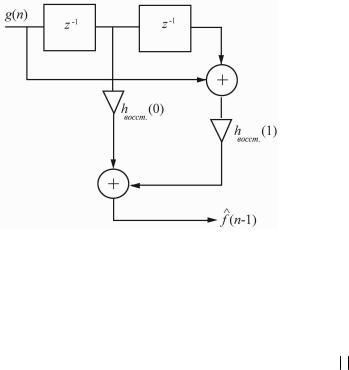
Полученный КИХ-фильтр может быть реализован с задержкой на один шаг в форме прямой свертки так, как показано на Рисунке

6.9.

Ошибка восстановления сигнала здесь опять определяется по формуле (6.16):

Достоинство нерекурсивных процедур восстановления состоит в простоте их расчета. Для построения восстанавливающего КИХ- фильтра достаточно решить систему линейных уравнений, а не решать сложную задачу факторизации энергетических спектров. Кроме того, как уже отмечалось, КИХ-фильтр может обеспечить качество восстановления более близкое к оптимальному чем физически реализуемый винеровский фильтр.

160

Еще одно достоинство заключается в том, что данная методика расчета процедур восстановления легко обобщается на случай обработки двумерных сигналов.

Рисунок 6.9 - КИХ-фильтр, реализованный в форме прямой свертки с задержками

6.7 Практические задания к разделу 6

Квазиоптимальное восстановление сигналов (КИХ-фильтр)

6.7.1. Модель наблюдения:

y(m) = x(m) + v(m) ,

x(m) - полезный сигнал с корреляционной функцией Rx (n) = 0,8 n , v(m) - белый шум с единичной дисперсией, не зависящий от полезного сигнала.

Построить квазиоптимальный КИХ-фильтр для области наблюдения D = {−1;1} . Записать уравнение оценивания. Рассчитать среднеквадратичную погрешность.

6.7.2. Дана модель наблюдения:

независимый от полезного сигнала.

161

Определить импульсную характеристику и построить структурную схему квазиоптимального КИХ-фильтра с областью

независимый от сигнала.

Построить квазиоптимальный восстанавливающий КИХ-фильтр с «окном» D = {−1; 0;1} . Определить среднеквадратичную ошибку оценивания полезного сигнала.

6.7.4. Модель наблюдения:

∞

y(m) = ∑2−k x(m − k) + v(m) . k =0

Полезный сигнал x(m) - некоррелированный с единичной дисперсией. Аддитивный шум v(m) – белый с дисперсией 3/5,

статистически независимый от полезного сигнала.

Построить квазиоптимальный КИХ-фильтр для восстановления сигнала x(m) . Область наблюдения D = {−1; 0;1} .

6.7.5. Дана модель наблюдения:

независимый от полезного сигнала.

Определить импульсную характеристику и построить структурную схему квазиоптимального КИХ-фильтра с областью наблюдения D = {−1; 0} . Определить среднеквадратичную ошибку оценивания полезного сигнала.

162