ЦОС учебник

вход поступает последовательность с математическим ожиданием, равным 1, и корреляционной функцией:

R (m) = δ(m −1) + 2δ(m) + δ(m + 1) .

Импульсная характеристика ЛИС-системы равна

h (n) = δ(n) − δ(n −1) .

5.4.4. На вход ЛИС-системы с импульсной характеристикой: h(n) = δ(n − 2) − δ(n − 3)

поступает сумма двух независимых случайных последовательностей:

(1)белый шум с нулевым математическим ожиданием и единичной дисперсией и

(2)последовательность с единичным математическим ожиданием, единичной дисперсией и экспоненциальной корреляционной функцией (коэффициент корреляции соседних отсчетов равен 0,8).

Определить математическое ожидание, дисперсию, корреляционную функцию и энергетический спектр выходной последовательности.

5.4.5.На вход ЛИС-системы с импульсной характеристикой:

h(n) = δ(n − 2) − αδ(n − 3)

поступает сумма двух независимых стационарных случайных последовательностей: дискретного белого шума с математическим ожиданием M1 и дисперсией D1 и последовательности с

математическим ожиданием M 2 и корреляционной функцией:

R(k ) = D2α k , a < 1 .

Определить математическое ожидание, дисперсию, корреляционную функцию и энергетический спектр выходной последовательности.

5.4.6. На вход ЛИС-системы с импульсной характеристикой: h(n) = αn−1u(n −1), α < 1 ,

123

поступает стационарная случайная последовательность с математическим ожиданием M x и корреляционной функцией:

Rx (k ) = Dx (ρ k ), ρ < 1 .

Определить математическое ожидание, дисперсию, корреляционную функцию и энергетический спектр выходной последовательности.

5.4.7. Стационарная случайная последовательность с математическим ожиданием M x и корреляционной функцией:

Rx (k ) = Dxδ(k )

поступает на вход ЛИС-системы с импульсной характеристикой h (n) = u (n) − u (n − 3) .

Определить математическое ожидание, дисперсию и корреляционную функцию случайной последовательности на выходе системы, а также взаимную корреляционную функцию входной и выходной последовательностей.

5.4.8. Стационарная случайная последовательность с математическим ожиданием M x и корреляционной функцией:

Rx (k ) = Dxα k , α < 1

поступает на вход ЛИС-системы с импульсной характеристикой h (n) = δ(n −10) + β δ(n −11) .

Определить математическое ожидание, дисперсию и корреляционную функцию случайной последовательности на выходе системы, а также взаимную корреляционную функцию входной и выходной последовательностей.

5.4.9. Стационарная случайная последовательность с математическим ожиданием M x и корреляционной функцией:

Rx (k ) = Dxα k , α < 1

поступает на вход ЛИС-системы с импульсной характеристикой h (n) = αn u (n) .

124

Определить математическое ожидание, дисперсию и корреляционную функцию случайной последовательности на выходе системы, а также взаимную корреляционную функцию входной и выходной последовательностей.

5.4.10. Стационарная случайная последовательность с математическим ожиданием M x и корреляционной функцией:

Rx (k ) = Dxδ(k )

поступает на вход ЛИС-системы с импульсной характеристикой: h (n) = (αn + βn ) u (n), α < 1, β < 1 .

Определить математическое ожидание, дисперсию и корреляционную функцию последовательности на выходе системы, а также взаимную корреляционную функцию входной и выходной последовательностей.

корреляционной функцией последовательности на выходе системы, а также взаимную корреляционную функцией входной и выходной последовательностей.

Факторизация энергетического спектра

5.4.12. Определить передаточную функцию и построить структурную схему ЛИС-системы, преобразующей стационарную случайную последовательность с корреляционной функцией

Rx (k ) = 0,5 k

в последовательность с корреляционной функцией

Ry (k) = 6δ(k ) + δ(k + 1) + δ(k −1) − 2δ(k + 2) − 2δ(k − 2) .

125

5.4.13. Определить передаточную функцию и построить структурную схему ЛИС-системы, преобразующей стационарную случайную последовательность с корреляционной функцией:

Rx (k ) = δ(k) + 2 [δ(k −1) + δ(k + 1)] 5

в последовательность с корреляционной функцией

Ry (k) = δ(k ) + 1 [δ(k −1) + δ(k + 1)] . 2

5.4.14. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей последовательность с корреляционной функцией:

Rx (k ) = δ(k ) + 12 (δ(k −1) + δ(k + 1))

в последовательность с корреляционной функцией:

Ry (k ) = α k , α < 1 .

5.4.15. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей последовательность с корреляционной функцией

последовательности, если входная имеет математическое ожидание

M x .

5.4.16. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей последовательность с корреляционной функцией

Rx (k ) = Dxδ(k )

в последовательность с корреляционной функцией

Ry (k ) = Dy δ(k ) + 0,5δ(k + 1) + 0,5δ(k −1) .

126

5.4.17. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей последовательность с корреляционной функцией

Rx (k ) = Dxδ(k )

в последовательность с корреляционной функцией

Ry (k ) = 0,5Dy (α k + β k ), α < 1, β < 1 .

5.4.18. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей последовательность с корреляционной функцией

Rx (k ) = 0,5Dx (α k + β k ), α < 1, β < 1

в последовательность с корреляционной функцией

Ry (k ) = Dyδ(k ) .

5.4.19.Построить ЛИС-систему, формирующую из белого шума случайную последовательность η(n) с корреляционной функцией

Rη (m) = 2− m cos π2 m .

5.4.20. Построить ЛИС-систему, формирующую из белого шума случайную последовательность η(n) с корреляционной функцией

Rη (m) = 2− m 1 + m2 .

5.4.21. Определить передаточную функцию, импульсную характеристику, построить структурную схему ЛИС-системы, преобразующей стационарную в широком смысле случайную последовательность x (n) с корреляционной функцией

Rx (k ) = δ(k ) + 12 (δ(k −1) + δ(k + 1))

в последовательность y (n) с корреляционной функцией

Ry (k ) = 2− k .

127

6 ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ И ВОССТАНОВЛЕНИЕ ИЗОБРАЖЕНИЙ

6.1 Восстановление дискретного сигнала ЛИС-системой

Пусть имеется полезный сигнал – последовательность f (n) .

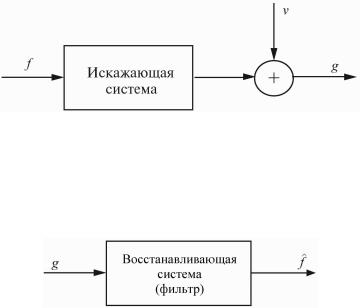
Однако непосредственному наблюдению (измерению) он недоступен. В нашем распоряжении имеется лишь сигнал g (n) –

результат прохождения сигнала через некоторую “ искажающую” систему, дополнительно искаженный шумом v(n) (см. Рисунок

6.1).

Рисунок 6.1 - Модель наблюдения полезного сигнала

Требуется восстановить полезный сигнал по наблюдаемому. Для этого необходимо синтезировать такую восстанавливающую систему (фильтр), чтобы при подаче на ее вход наблюдаемого

Рисунок 6.2 - Схема восстанавливающей системы

Далее мы сузим класс рассматриваемых сигналов и систем. Во-первых, в большинстве практически важных случаев

искажения сигнала удается описать моделью ЛИС-системы, рассмотрением которой мы и ограничимся. Будем считать, что

128

известна ее импульсная характеристика h (n) . Тогда наблюдаемая последовательность запишется в виде:

Соотношение (6.1) задает так называемую линейную модель наблюдения в дискретном времени.

Во-вторых, восстанавливать сигнал будем также при помощи ЛИС-системы:

где hвосст (n) - импульсная характеристика восстанавливающей ЛИС-системы.

В-третьих, и полезный сигнал f (n) , и шум v (n) будем считать

стационарными случайными последовательностями, статистические характеристики которых известны.

Заметим, что, поскольку все преобразуемые последовательности случайны, то и ошибка восстановления:

в каждый момент времени случайна. Мы будем строить такой восстанавливающий фильтр, который обеспечивает минимум ошибки в среднеквадратичном смысле, то есть минимизирует ее дисперсию:

Из всего сказанного наиболее существенным является ограничение, заключающееся в требовании линейности восстанавливающей системы. Однако для нелинейных систем получить конкретные результаты их синтеза гораздо сложнее. Кроме того из теории информации известно, что для важного класса сигналов – гауссовских – оптимальное (наилучшее) в среднеквадратичном смысле восстановление обеспечивается именно линейной системой.

ЛИС-система, реализующая преобразование (6.2) и обеспечивающая при этом выполнение условия (6.4), называется

"оптимальным линейным восстанавливающим фильтром". А ее

129

применение реализует процедуру оптимального линейного восстановления.

Очень часто однако на импульсную характеристику восстанавливающей ЛИС-системы налагаются дополнительные ограничения, связанные с удобством реализации. Например, требуется, чтобы она была КИХ-системой или физически реализуемой БИХ-системой (см.п.4.3). В таких ситуациях ошибка восстановления несколько возрастет, то есть мы получим квазиоптимальные процедуры восстановления.

Мы объединим рассмотрение оптимального и квазиоптимального восстановления следующим образом: будем считать, что импульсная характеристика восстанавливающая ЛИС- системы отлична от нуля для значения аргумента из некоторого множества D (интервала наблюдения):

Определим при этом ограничении параметры системы, минимизирующие ошибку восстановления. С учетом сказанного выше конкретизируется формула (6.2)

Минимизация ошибки осуществляется, путем варьирования ненулевых отсчетов импульсной характеристики восстанавливающей системы. В точке минимума обеспечивается равенство нулю всех частных производных:

Подставив (6.7) в (6.8), получаем:

130

то есть взаимная корреляционная функция Bεg (m) = 0 , ошибка

оптимального восстановления некоррелирована с наблюдаемым сигналом. Это утверждение известно в теории оценивания как

"лемма об ортогональном проецировании", которая будет нам полезна в дальнейшем.

Во-вторых, перенеся в (6.9) вычитаемое в правую часть после применения оператора математического ожидания, получим:

– уравнение Винера-Хопфа для дискретных систем.

Таким образом, импульсная характеристика оптимального линейного восстанавливающего (или квазиоптимального) фильтра определяется из системы, состоящей из уравнения Винера-Хопфа и ограничений, налагаемых на импульсную характеристику:

Различный вид области D приводит к существенно различным методам решения системы (6.12). Определим ошибку восстановления сигнала оптимальным линейным фильтром, продолжив преобразования, входящие в (6.7), с учетом (6.3) и (6.10):

131

Рассмотрим важный частный случай, когда имеет место упрощенная модель наблюдения с белым шумом, независимым от сигнала:

и нулевой отсчет импульсной характеристики hвосст (0) не равен нулю, ({0} D ) . В этом случае

Bg (k ) = B f (k ) + Bv (k ) = B f (k ) + σv2δ(k ) ,

Bfg (k ) = E { f (n) g (n + k )} = E{ f (n) f (n + k ) + v (n + k )} =

=E{ f (n) f (n + k )} + E{ f (n)v (n + k )} = B f (k ) = B f (−k ).

ииз уравнения Винера-Хопфа (6.11) получаем:

∑hвосст (k ) B f (m − k ) + σv2δ(m − k ) = B f (m) , k D

∑hвосст (k ) B f (m − k ) + σv2 hвосст. (m) = B f (m) k D

и при m = 0 :

132