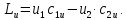2.6 Уравнение моментов количества движения

Из теоретической механики известно, что равнодействующая всех сил R, действующих на тело массойm_Tи скоростьюс_T, отстоящее от оси вращения на расстоянииr, создает крутящий момент относительно осиО-О(рисунок 2.20):

2.6.1

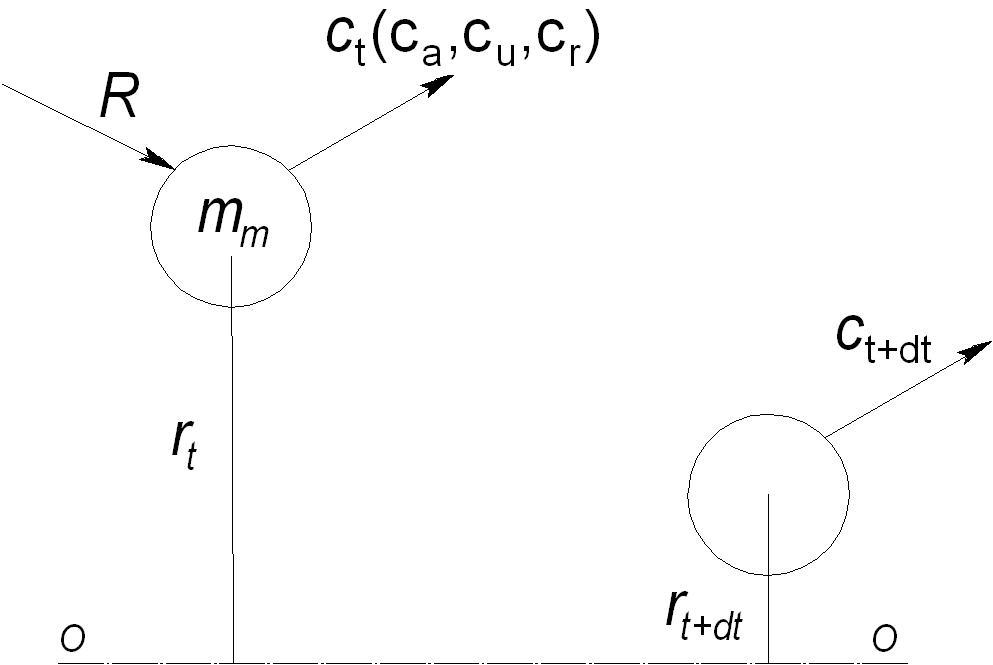
Рисунок 2.20 – К пояснению понятия момента количества движения

Крутящий момент равен изменению момента количества движения в единицу времени:

2.6.2

Рассмотрим участок стационарного потока рабочего тела в канале межлопаточном произвольной формы (рисунок 2.3). Его форма, а также все параметры потока на входе и выходе известны. Рассматриваемый участок разделяется на бесконечное число элементарных струек. Каждая из них представляет собой цилиндр с криволинейной образующей, поперечное сечение которого настолько мало, что значения параметров потока в любой его точке можно считать одним и тем же.

Рассмотрим течение рабочего тела через любую случайно выбранную элементарную струйку. В начальный момент времени выделенный объем находился в положении 1-2. Через бесконечно малый отрезок времениdtон переместиться в положение 3-4 (рисунок 2.21). Отрезок времениdtпринимается настолько малым, что параметры потока в каждом сечении в его начальный и конечный момент можно считать неизменными (с_1u= с_3u;с_2u= с_4u;r₂=r₄;r₁=r₃и т.д.).

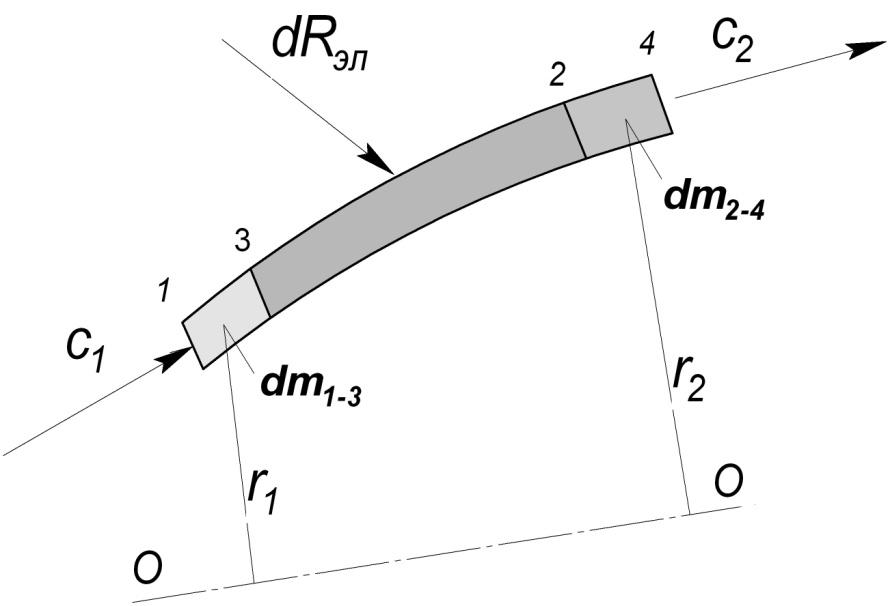
Рисунок 2.21 – Схема течения в канале произвольной формы

Равнодействующая сил, действующая на рассматриваемую струйку 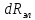, относительно осиО-Осоздает крутящий момент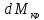

Как видно из рисунка 2.21, область 3-2является общей для начального и конечного положения рабочего тела. Поэтому рассматриваемое движение может быть представлено следующим образом: в неизменный в теченииdtвремени объем3-2втекает объем1-3и вытекает2-4. То есть, изменение момента количества движения рассматриваемой струйки относительно осиО-О за времяdtравно разности моментов количества движения масс1-3и2-4 относительно той же оси:

2.6.3

Поскольку рассматривается установившееся движение, то . Учитывая, что отношение массы элемента ко времени равно расходу рабочего тела через элементарную струйку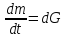окончательно имеем:

2.6.4

Запишем для всех струек уравнения моментов количества движения и сложим между собой. Если для всех элементарных струек одинаковы значения 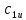и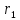, а на выходе одинаковыи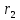, тогда получим:

2.6.5

Умножим обе части последнего уравнения на величину угловой скорости , затем разделим обе части на расход рабочего телаG.

2.6.6

Левая часть уравнения представляет собой удельную работу на окружности колеса элементарного лопаточного венца:

Кроме того, учитывая, что произведение угловой скорости на радиусrравно окружной скорости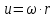, окончательно получим:

2.6.7а

Данное уравнение называется уравнением моментов количества движения применительно к лопаточным машинам. Оно было также выведено Л. Эйлером.

Это уравнение устанавливает связь работы, передаваемой лопатками потоку, с кинематическими параметрами потока.

Для осевых лопаточных машин . Поэтому уравнение примет вид:

2.6.7б

Запишем это уравнение применительно к компрессору и турбине. Форма записи для компрессора полностью совпадает с канонической формой (2.6.7). В турбине же работа совершается газом по вращению РК, поэтому знаки в правой части меняются на противоположные ().

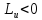Окончательно имеем для компрессора:

;

2.6.8к

для турбины:

2.6.8т

Сопоставляя уравнения 2.6.8к и 2.6.8т можно сделать выводу о том, что компрессор и турбина являются обращенными машинами, поскольку уравнения описывающие процессы в них имеют одинаковую форму, но имеют разные знаки.

Полученные уравнения имеют большое значение в теории турбомашин. Несомненным достоинством уравнения моментов количества движения является то, что его использование не требует знания распределения давления по поверхности лопаток. Надо только знать кинематические параметры на входе и выходе из РК.
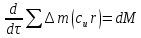
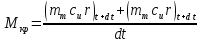
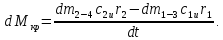
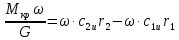
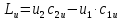