- •Глава 2 – Базовые уравнения теории лопаточных машин и общие закономерности их рабочего процесса
- •2.1 Газодинамические функции
- •2.1.1 Параметры торможения
- •2.1.2 Безразмерные скорости в теории турбомашин
- •2.1.3 Газодинамические функции
- •2.2 Уравнение неразрывности
- •2.3 Уравнения сохранения энергии
- •2.3.1 Уравнение энергии в механической форме в абсолютном движении
- •2.3.2 Уравнение энергии в механической форме в относительном движении
- •2.3.3 Уравнение энергии в тепловой форме в абсолютном движении
- •2.3.4 Уравнение энергии в тепловой форме в относительном движении
- •2.4 Уравнение количества движения
- •2.6 Уравнение моментов количества движения
- •2.6.1 Основные выводы из уравнения моментов количества движения
- •2.6.2 Влияние частоты вращения на работу ступени
- •2.6.3 Понятие о треугольниках скоростей
- •2.6.4 Влияние разности на работу ступени
- •2.7 Основные закономерности течения газа в межлопаточных каналах и механизмы возникновения потерь
- •2.7.1 Потери трения и концевые потери
- •2.7.2 Кромочные потери
- •2.7.3 Потери связанные с отрывом потока
- •2.7.4 Волновые потери
- •2.7.5 Вторичные потери
- •2.7.6 Потери в радиальном зазоре
- •2.7.7 Потери в осевом зазоре
- •2.7.8 Дисковые потери
- •2.8 Важнейшие формулы главы №2
2.3.3 Уравнение энергии в тепловой форме в абсолютном движении
Запишем
уравнение сохранение энергии в
механической форме в абсолютном движении
в дифференциальном виде (2.3.6). При этом
учтем, что плотность обратно пропорциональна
удельному объему
 :
:
|
|
|
2.3.22 |
Энергия,
расходуемая в реальном процессе на
преодоление гидравлических потерь
 ,
независимо от природы потерь, в конечном
итоге преобразуется в тепло и подводится
к рабочему телу (
,
независимо от природы потерь, в конечном
итоге преобразуется в тепло и подводится
к рабочему телу (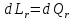 ).
Это единственный источник тепла,
подводимого к потоку в лопаточных
машинах
).
Это единственный источник тепла,
подводимого к потоку в лопаточных
машинах .
.
Согласно
первому закону термодинамики подводимое
тепло идет на совершение работы
 по изменению объема рабочего тела и
изменение внутренней энергии
по изменению объема рабочего тела и
изменение внутренней энергии :
:
|
|
|
2.3.23 |
Подставив уравнение 2.3.23 в 2.3.22 получим:
|
|
|
|
|
|
|
|
Сумма
 представляет собой энтальпию -термодинамический
потенциал,
характеризующий состояние системы в
термодинамическом равновесии при выборе
в качестве независимых
переменных давления, энтропии и
числа частиц. Другими словами это
количество
энергии, которая доступна для преобразования
в теплоту при определенной температуре
и давлении.
представляет собой энтальпию -термодинамический
потенциал,
характеризующий состояние системы в
термодинамическом равновесии при выборе
в качестве независимых
переменных давления, энтропии и
числа частиц. Другими словами это
количество
энергии, которая доступна для преобразования
в теплоту при определенной температуре
и давлении.
Учитывая
сказанное выше, а также то, что сумма
энтальпии и кинетической энергии
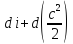 является энтальпией по заторможенным
параметрам
является энтальпией по заторможенным
параметрам
|
|
|
2.3.24 |
Интегрируя последнее уравнение на конечном участке пути частицы от входа «1» до выхода «2», окончательно получаем:
|
|
|
2.3.25 |
Это уравнение называется уравнением сохранения энергии в тепловой форме в абсолютном движении.
Из
этого уравнения следует, что полная
температура
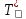 меняется только тогда, когда в рабочем
процессе подводится/отводится тепло
и/или работа. Применительно к лопаточным
машинам это означает, что температура
заторможенного потока будет меняться
только в рабочем колесе. В НА и СА она
сохранится постоянной.
меняется только тогда, когда в рабочем
процессе подводится/отводится тепло
и/или работа. Применительно к лопаточным
машинам это означает, что температура
заторможенного потока будет меняться
только в рабочем колесе. В НА и СА она
сохранится постоянной.
Также
следует отметить, что на величину полной
температуры
 в отличие от полного давления
в отличие от полного давления не влияют потери энергии в потоке
не влияют потери энергии в потоке .
.
2.3.4 Уравнение энергии в тепловой форме в относительном движении
Запишем
уравнение сохранение энергии в
механической форме в относительном
движении в дифференциальном виде
(2.3.18). При этом учтем, что плотность
обратно пропорциональна удельному
объему
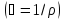 :
:
|
|
|
2.3.26 |
Энергия,
расходуемая в реальном процессе на
преодоление гидравлических потерь
 ,
независимо от природы потерь, в конечном
итоге преобразуется в тепло и подводится
к рабочему телу (
,
независимо от природы потерь, в конечном
итоге преобразуется в тепло и подводится
к рабочему телу ( ).
Это единственный источник тепла,
подводимого к потоку в лопаточных
машинах
).
Это единственный источник тепла,
подводимого к потоку в лопаточных
машинах .
.
Согласно
первому закону термодинамики подводимое
тепло идет на совершение работы
 по изменению объема рабочего тела и
изменение внутренней энергии
по изменению объема рабочего тела и
изменение внутренней энергии :
:
|
|
|
2.3.27 |
Подставив уравнение 2.3.27 в 2.3.26 получим:
|
|
|
|
|
|
|
|
Как
отмечалось в разделе 2.3.3 сумма
 представляет собой энтальпию. Поэтому
окончательно имеем:
представляет собой энтальпию. Поэтому
окончательно имеем:
|
|
|
2.3.28 |
Сумма энтальпии и кинетической энергии потока в относительном движении представляет собой энтальпию потока заторможенного в относительном движении:
|
|
|
2.3.29 |
где
 - температура потока, заторможенного в
относительной СК.
- температура потока, заторможенного в
относительной СК.
Поэтому окончательно имеем:
|
|
|
2.3.30 |
Интегрируя последнее уравнение на конечном пути частицы от входа «1» до выхода из ЛВ «2», окончательно получаем:
|
|
|
2.3.31 |
Это уравнение называется уравнением сохранения энергии в тепловой форме в относительном движении.
Следствие №1. Из данного уравнения следует, что работа инерционных сил и подводимое в процессе тепло идут на изменение энтальпии и на изменение кинетической энергии потока в относительном движении.
Следствие
№2.
Также анализируя уравнения 2.3.30 и
2.3.31 можно заключить, что температура
потока заторможенного в относительном
движении не зависит от аэродинамического
совершенства лопаточной машины и
меняется только при подводе тепла и
действии инерционных сил.
не зависит от аэродинамического
совершенства лопаточной машины и
меняется только при подводе тепла и
действии инерционных сил.
Следствие
№3.Рассмотрим элементарную решетку рабочего
колеса ЦБК (рисунок 2.18). Лопатки РК –
неохлаждаемые, т.е. внешнее тепло к
потоку не подводится ( ).
Уравнение энергии в тепловой форме в
относительном движении для данного
случая имеет вид:
).
Уравнение энергии в тепловой форме в
относительном движении для данного
случая имеет вид:
|
|
|
2.3.32 |

Рисунок 2.18 – Элементарная решетка РК ЦБК
Учитывая,
что в ЦБК рабочее тело движется от
меньшего диаметра к большему ( )
и тормозится в относительном движении
)
и тормозится в относительном движении ,
то
,
то и
и .
Отсюда из уравнения 2.3.32 следует, что
.
Отсюда из уравнения 2.3.32 следует, что .
То есть в РК ЦБК статическая температура
возрастает из-за торможения потока в
относительном движении и из-за работы
инерционных сил.
.
То есть в РК ЦБК статическая температура
возрастает из-за торможения потока в
относительном движении и из-за работы
инерционных сил.
Если
уравнение энергии записать для осевого
компрессора
 ,
то оно будет иметь вид:
,
то оно будет иметь вид:
|
|
|
2.3.33 |
Отсюда можно сделать вывод, что температура в РК осевого компрессора растет только из-за торможения потока в относительном движении.