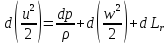- •Глава 2 – Базовые уравнения теории лопаточных машин и общие закономерности их рабочего процесса
- •2.1 Газодинамические функции
- •2.1.1 Параметры торможения
- •2.1.2 Безразмерные скорости в теории турбомашин
- •2.1.3 Газодинамические функции
- •2.2 Уравнение неразрывности
- •2.3 Уравнения сохранения энергии
- •2.3.1 Уравнение энергии в механической форме в абсолютном движении
- •2.3.2 Уравнение энергии в механической форме в относительном движении
- •2.3.3 Уравнение энергии в тепловой форме в абсолютном движении
- •2.3.4 Уравнение энергии в тепловой форме в относительном движении
- •2.4 Уравнение количества движения
- •2.6 Уравнение моментов количества движения
- •2.6.1 Основные выводы из уравнения моментов количества движения
- •2.6.2 Влияние частоты вращения на работу ступени
- •2.6.3 Понятие о треугольниках скоростей
- •2.6.4 Влияние разности на работу ступени
- •2.7 Основные закономерности течения газа в межлопаточных каналах и механизмы возникновения потерь
- •2.7.1 Потери трения и концевые потери
- •2.7.2 Кромочные потери
- •2.7.3 Потери связанные с отрывом потока
- •2.7.4 Волновые потери
- •2.7.5 Вторичные потери
- •2.7.6 Потери в радиальном зазоре
- •2.7.7 Потери в осевом зазоре
- •2.7.8 Дисковые потери
- •2.8 Важнейшие формулы главы №2
2.3.2 Уравнение энергии в механической форме в относительном движении
Рассмотрим
установившееся стационарное течение
рабочего тела через рабочее колесо
произвольной лопаточной машины. Рабочее
колесо вращается с постоянной угловой
скоростью .
В потоке вблизи поверхности пера лопатки
выделим произвольную бесконечно малую
частицуА, движущуюся со скоростью в системе координат вращающейся вместе
с РК с угловой скоростью.
В указанной СК точка движется по
траекторииSw.
Вектор скорости
в системе координат вращающейся вместе
с РК с угловой скоростью.
В указанной СК точка движется по
траекторииSw.
Вектор скорости направлен по касательной к линии токаSwв рассматриваемой точке.
направлен по касательной к линии токаSwв рассматриваемой точке.
В рассматриваемой точке введем локальную систему координат Aswnwlw, осьAswкоторой направлена по касательной к линии тока в точке А, осьAnwнормаль к траектории движения частицыSw, а осьAlwперпендикулярна первым двум (рисунок 2.14).
Вокруг рассматриваемой точки выделим бесконечно малый объем, имеющий форму параллелепипеда, ориентированный вдоль осей локальной СК, со сторонами размерами dsw, dnw, dlwи центром в начале координат (рисунок 2.15). Масса выделенного объема составляет:
|
|
|
2.3.12 |

Рисунок 2.14 – Рассматриваемая частица рабочего тела
Поскольку выделенный объем рассматривается в подвижной СК, то согласно принципу Даламбера, при составлении уравнения равновесия для получения уравновешенной системы к активным силам, действующим на объем. необходимо прибавить силы инерции.
На выделенный объем действуют следующие силы (рисунок 2.15):
 – сила, с которой лопатка действует на
частицу, направленная перпендикулярно
траектории движения(
– сила, с которой лопатка действует на
частицу, направленная перпендикулярно
траектории движения(
 );
);
 – сила давления, с которой среда
воздействует на частицу;
– сила давления, с которой среда
воздействует на частицу;
 – сила трения, направленная по касательной
к линии тока.
– сила трения, направленная по касательной
к линии тока.
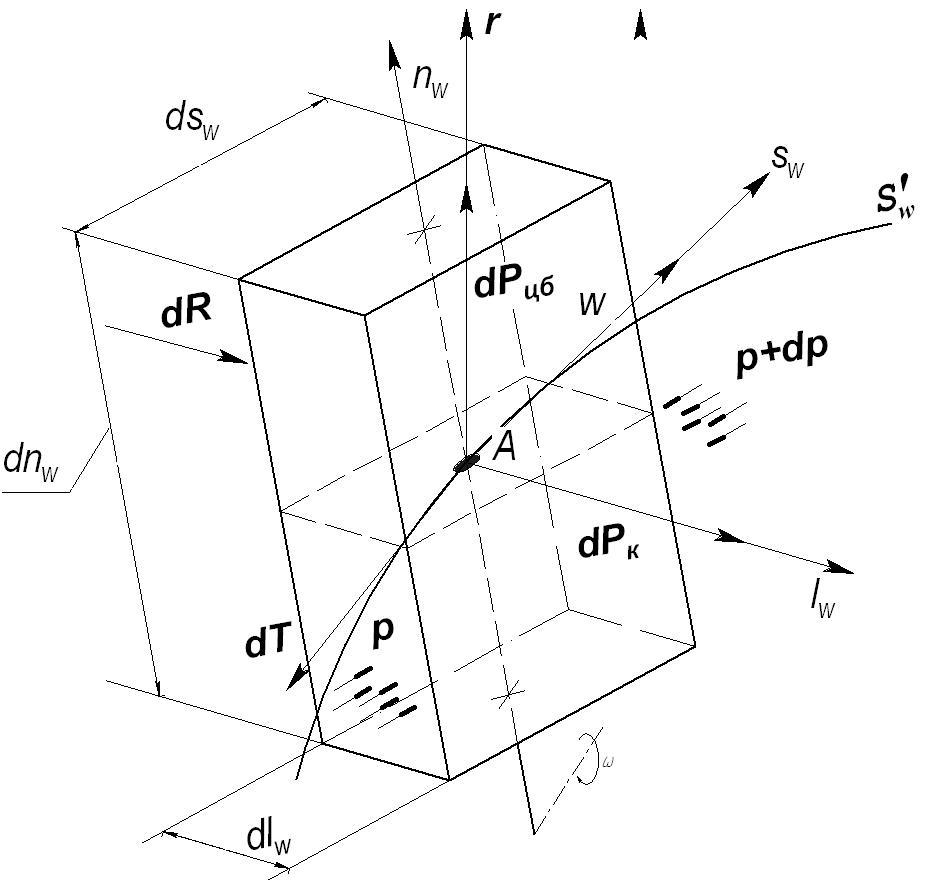
Рисунок 2.15 – Схема сил, действующих на выделенный объем в подвижном РК
Перечисленные
силы являются активными. Кроме того на
выделенный объем действуют две инерционных
силы: центробежная
 и сила Кариолиса
и сила Кариолиса .
.
Центробежная
сила
 ,
направлена вдоль радиуса от центра к
периферии. Ее величина может быть найдена
по формуле:
,
направлена вдоль радиуса от центра к
периферии. Ее величина может быть найдена
по формуле:
|
|
|
2.3.13 |
где r– расстояние от оси вращения до центра масс рассматриваемой частицы.
Сила
Кариолиса
 перпендикулярная вектору относительной
скорости
перпендикулярная вектору относительной
скорости (
( )
и вектору угловой скорости
)
и вектору угловой скорости (
( ).
Ее величина может быть найдена по
следующей формуле:
).
Ее величина может быть найдена по
следующей формуле:
|
|
|
2.3.14 |
В относительной СК выделенный объем движется ускоренно под действием указанных выше сил. Данное обстоятельство позволяет записать для рассматриваемого случая уравнение второго закона Ньютона:
|
|
|
2.3.15 |
Рассмотрим чему равны проекции перечисленных сил на ось Asw локальной СК:
вектор
 перпендикулярен вектору скорости
перпендикулярен вектору скорости ,
который лежит на осиAsw.
По этой причине проекция
,
который лежит на осиAsw.
По этой причине проекция ;
;сила трения направлена вдоль касательной к линии тока в сторону противоположную движению, поэтому
 ;
;сила Кориолиса
 по определению направлена перпендикулярно
направлению вектора скорости
по определению направлена перпендикулярно
направлению вектора скорости и по этой причине ее проекция на осьAswтакже равна нулю
и по этой причине ее проекция на осьAswтакже равна нулю ;
;проекция сил давления на ось oswявляется разностью сил давления, действующих на поверхности выделенного объема перпендикулярные указанной оси. Такими поверхностями являются грани со сторонами
 и
и (рисунок 2.15). На поверхность находящуюся
ниже по потоку действует сила
(рисунок 2.15). На поверхность находящуюся
ниже по потоку действует сила ,
а на поверхность выше по течению –
,
а на поверхность выше по течению – .
Следует обратить внимание на то, что
эти силы действуют в противоположных
направлениях, поэтому проекция сил
давления на осьAsw,действующая на выделенный объем, равна:
.
Следует обратить внимание на то, что
эти силы действуют в противоположных
направлениях, поэтому проекция сил
давления на осьAsw,действующая на выделенный объем, равна:

Проекция центробежной силы на ось Aswбудет равна:

где
 - угол между осьюoswи радиальным направлением (рисунок
2.16). Определим чему он равен. За бесконечно
малое времяdtчастица
переместится в направленииAswна
- угол между осьюoswи радиальным направлением (рисунок
2.16). Определим чему он равен. За бесконечно
малое времяdtчастица
переместится в направленииAswна проекция этого перемещения на осьrравнаdr. Из прямоугольного
треугольника (рисунок 2.16) очевидно, что
проекция этого перемещения на осьrравнаdr. Из прямоугольного
треугольника (рисунок 2.16) очевидно, что
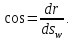
Учитывая сказанное выше, спроецируем уравнение 2.3.15 на ось Aswи получим:
|
|
|
2.3.16 |

Рисунок
2.16 – К определению угла

Поделив
обе части уравнения на
 и умножив их на
и умножив их на придем к следующему выражению:
придем к следующему выражению:
|
|
|
2.3.17 |
Принимая во внимание, что произведение силы на перемещение представляют собой работу, то слагаемым уравнения 2.3.17 можно придать следующий физический смысл:
 - удельная работа, затраченная на
преодоление сил трения;
- удельная работа, затраченная на
преодоление сил трения;
 – работа по изменению давления (т.е.
работа по расширению или сжатию);
– работа по изменению давления (т.е.
работа по расширению или сжатию);
 - удельная работа инерционных сил;
- удельная работа инерционных сил;
 - изменение удельной кинетической
энергии потока в относительном движении.
- изменение удельной кинетической
энергии потока в относительном движении.
Учитывая это, уравнение 2.3.17 примет вид:
|
|
|
2.3.18 |
Интегрируя последнее уравнение на конечном участке от входной границы «1» до выхода из ЛВ «2» окончательно получаем:
|
|
|
2.3.19 |
Это уравнение называется уравнением сохранения энергии в механической форме в относительном движении. Его используют только применительно к потоку в рабочих колесах.
Следствие №1:Запишем уравнение сохранения энергии в механической форме в относительном движении применительно к РК компрессора:
|
|
|
2.3.20к |
Из
этого уравнения следует, что изменение
потенциальной энергии сил давления
(другими словами повышение давления)
происходит за счет двух основных
составляющих: движения рабочего тела
в поле действия инерционных сил
 и торможения потока в относительном
движении
и торможения потока в относительном
движении ,
вопреки гидравлическому сопротивлению
,
вопреки гидравлическому сопротивлению .
.
Основываясь на сделанном выводе, сравним рабочий процесс в РК центробежного и осевого компрессоров (рисунок 2.17)
|
Центробежный |
Осевой |
|
|
|
|
|
|
|
|
|
Рисунок 2.17 – Сравнение осевого и центробежного компрессоров
В
центробежном компрессоре рабочее тело
входит в РК на радиусе
 ,
а выходит на радиусе
,
а выходит на радиусе ,
который существенно больше первого.
Данное обстоятельство говорит том, что
окружная скорость на выходе РК существенно
больше, чем на ее входе
,
который существенно больше первого.
Данное обстоятельство говорит том, что
окружная скорость на выходе РК существенно
больше, чем на ее входе и, следовательно, действие инерционных
сил в РК является существенным фактором,
повышающим давление в ЦБК. В осевом
компрессоре рабочее тело входит в РК и
покидает его на близких радиусах, что
обуславливает примерное равенство
окружных скоростей. В результате действие
инерционных сил в таком компрессоре
оказывается незначительным.
и, следовательно, действие инерционных
сил в РК является существенным фактором,
повышающим давление в ЦБК. В осевом
компрессоре рабочее тело входит в РК и
покидает его на близких радиусах, что
обуславливает примерное равенство
окружных скоростей. В результате действие
инерционных сил в таком компрессоре
оказывается незначительным.
Таким
образом, повышение давления в РК ЦБК
происходит за счет торможения потока
в относительном движении и за счет
действия инерционных сил. В то же время
в РК осевого компрессора давление растет
только за счет торможения потока в
относительном движении. По этой причине
степень сжатия
 осевого компрессора меньше степени
повышения давления ЦБК.
осевого компрессора меньше степени
повышения давления ЦБК.
Следствие №2:Запишем уравнение сохранения энергии в механической форме в относительном движении применительно к турбине:
|
|
|
2.3.20т |
Из
этого уравнения следует, что работа
расширения газа в РК турбины идет на
преодоление инерционных сил
 ,
ускорение потока в относительном
движении
,
ускорение потока в относительном
движении и на преодоление гидравлического
сопротивления
и на преодоление гидравлического
сопротивления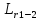 .
.
Следствие №3:Подставляя уравнение 2.3.20к и 2.3.20т в 2.3.6 можно получить еще одно важное соотношение для механической работы:
|
|
|
2.3.21к |
То есть подводимая работа в РК компрессора тратится на изменение кинетической энергии потока как в РК и НА.
|
|
|
2.3.21т |
Удельная теоретическая работа, совершаемая газом на лопатках РК турбины, получается за счет изменения кинетической энергии в СА и РК.
Сравнивая уравнения 2.3.21к и 2.3.21т видно, что эти уравнения одинаковы и отличаются только знаками (которые диаметрально противоположны). Отсюда можно сделать вывод, что компрессор и турбина являются обращенными машинами. Это означает, что их рабочий процесс аналогичен, но обращен.