
- •Отчет о лабораторном практикуме по линейному программированию
- •Ход работы.
- •Лабораторная работа №2.
- •Ход работы.
- •Лабораторная работа №3.
- •Ход работы.
- •Лабораторная работа №4 Технология решения задач линейного программирования симплекс – методом в табличном процессоре excel
- •Лабораторная работа №5 Решение злп методом искусственного базиса. Двойственность в злп.
- •Ход работы.
- •Лабораторная работа №6 Решение задач целочисленного линейного программирования в табличном процессоре Еxcel.
- •Ход работы.
- •Лабораторная работа №7 Технология решение транспортной злп в табличном процессоре Еxcel.
- •Ход работы.
- •Лабораторная работа №8 Решение транспортной задачи линейного программирования методом потенциалов в табличном процессоре Excel
МИНИСТЕРСТВО ОБРАЗОВАНИЯ ИНАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ АКАДЕМИКА С.П.КОРОЛЕВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)» (СГАУ)
Отчет о лабораторном практикуме по линейному программированию
Выполнил группа Проверила Клентак Л.С.
Самара, 2013
ОГЛАВЛЕНИЕ
Лабораторная работа №1. 3
Лабораторная работа №2. 6
Лабораторная работа №3. 9
ЛАБОРАТОРНАЯ РАБОТА №4 12
ЛАБОРАТОРНАЯ РАБОТА №5 16
ЛАБОРАТОРНАЯ РАБОТА №6 22
ЛАБОРАТОРНАЯ РАБОТА №7 28
ЛАБОРАТОРНАЯ РАБОТА №8 32
Лабораторная работа №1.
Технология решения задачи линейного программирования в табличном процессоре EXCEL.
Цель работы.
Ознакомиться с разделом математики «линейное программирование» как главным инструментом оценки эффективности управленческих решений, освоить технологии решения задач линейного программирования в табличном процессоре Excel.
Содержание лабораторной работы.
В работе необходимо решить оптимизационную задачу линейного программирования (ЗЛП) с использованием встроенных функций табличного процессора Excel и проинтерпретировать полученные решение, сравнив его эффективность с различными начальными приближениями.
Задание на лабораторную работу.
Вариант 6.
Целевая функция:
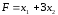 →max
→max
Система ограничений:
 ,
при условии
,
при условии
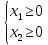
Ход работы.
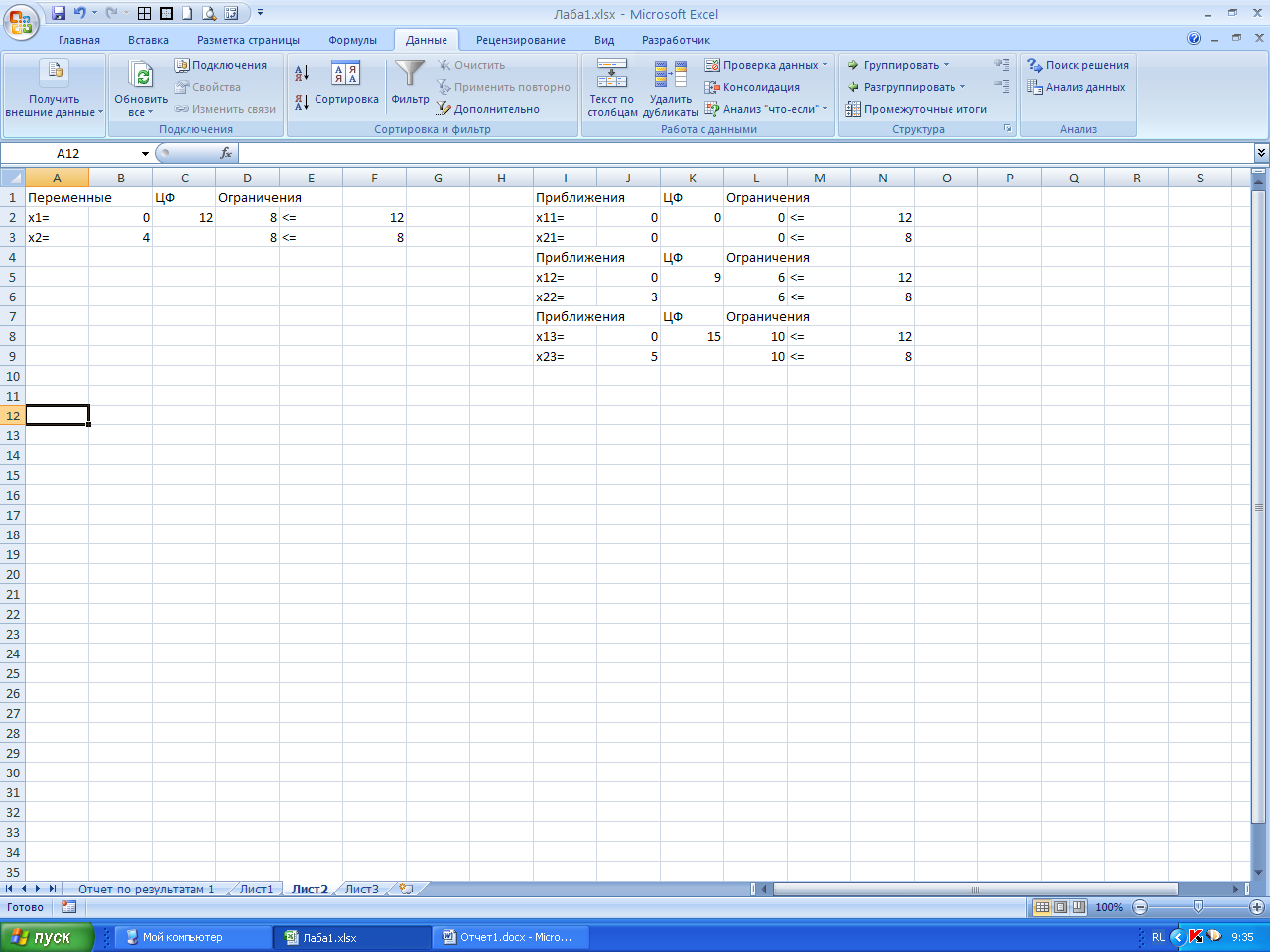
Рисунок 1 – Значение целевой функции при трех начальных приближениях
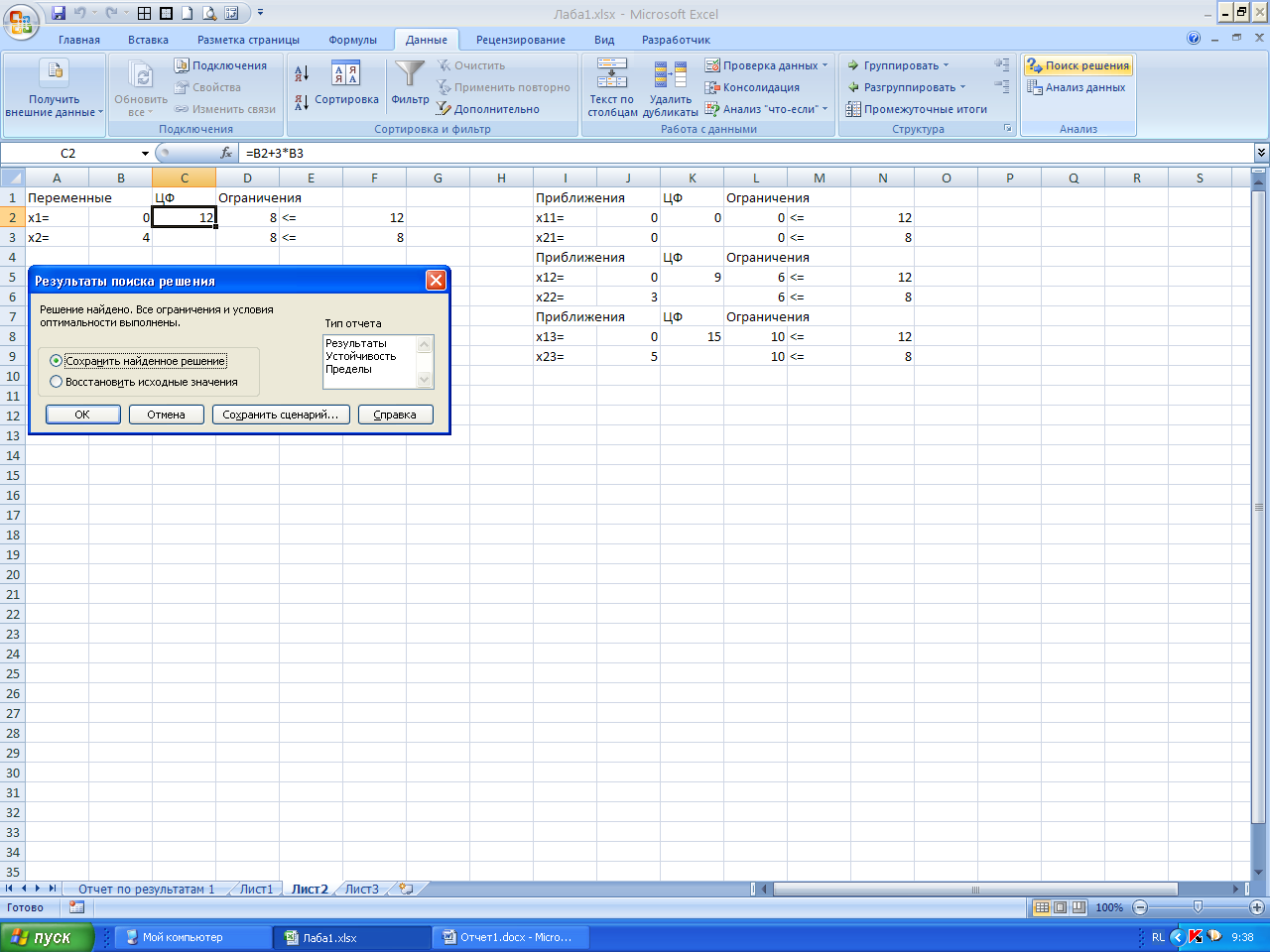
Рисунок 2 – Результат выполнения «поиска решений»

Рисунок 3 – Отчет по результатам поиска решений
Результат: оптимальные значения вычисленных неизвестных - x1=0и x2=4, целевая функция Fmax=12.
Ответы на контрольные вопросы.
С помощью какой встроенной функции EXCEL решаются оптимизационные задачи?
Оптимизационные задачи в Excel решаются с помощью встроенной функции «Поиск решений».
Как связана целевая ячейка с другими ячейками этого рабочего листа?
Целевая ячейка содержит в себе целевую функцию, значение которой вычисляется с помощью встроенной функции Excel «поиск решений», значение для которой используется из других ячеек рабочего листа, связанных с целевой ячейкой.
Наибольшее или наименьшее значение можно найти, используя встроенную функцию «Поиск решения»?
С помощью функции поиска решений можно найти как наибольшее, так и наименьшее значение.
Лабораторная работа №2.
Цель работы.
Освоить понятия математической модели задачи линейного программирования, ознакомиться с различными формами записи задачи линейного программирования, решить задачи линейного программирования в табличном процессоре EXCEL.
Содержание лабораторной работы.
Найдено решение задачи линейного программирования с помощью встроенной функции «Поиск решения» табличного процессора Excel.
Задание на лабораторную работу.
Вариант 6.
|
Вид сырья |
Запас сырья |
Расход на ед. продукции |
Прибыль от реализации | ||
|
П1 |
П2 |
Д1 |
Д2 | ||
|
1 |
25 |
1 |
5 |
1 |
2 |
|
2 |
9 |
1 |
1 | ||
|
3 |
21 |
3 |
1 | ||
ЗЛП в канонической форме:
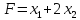 →max
→max
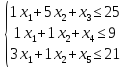 ,
,
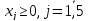
Ход работы.
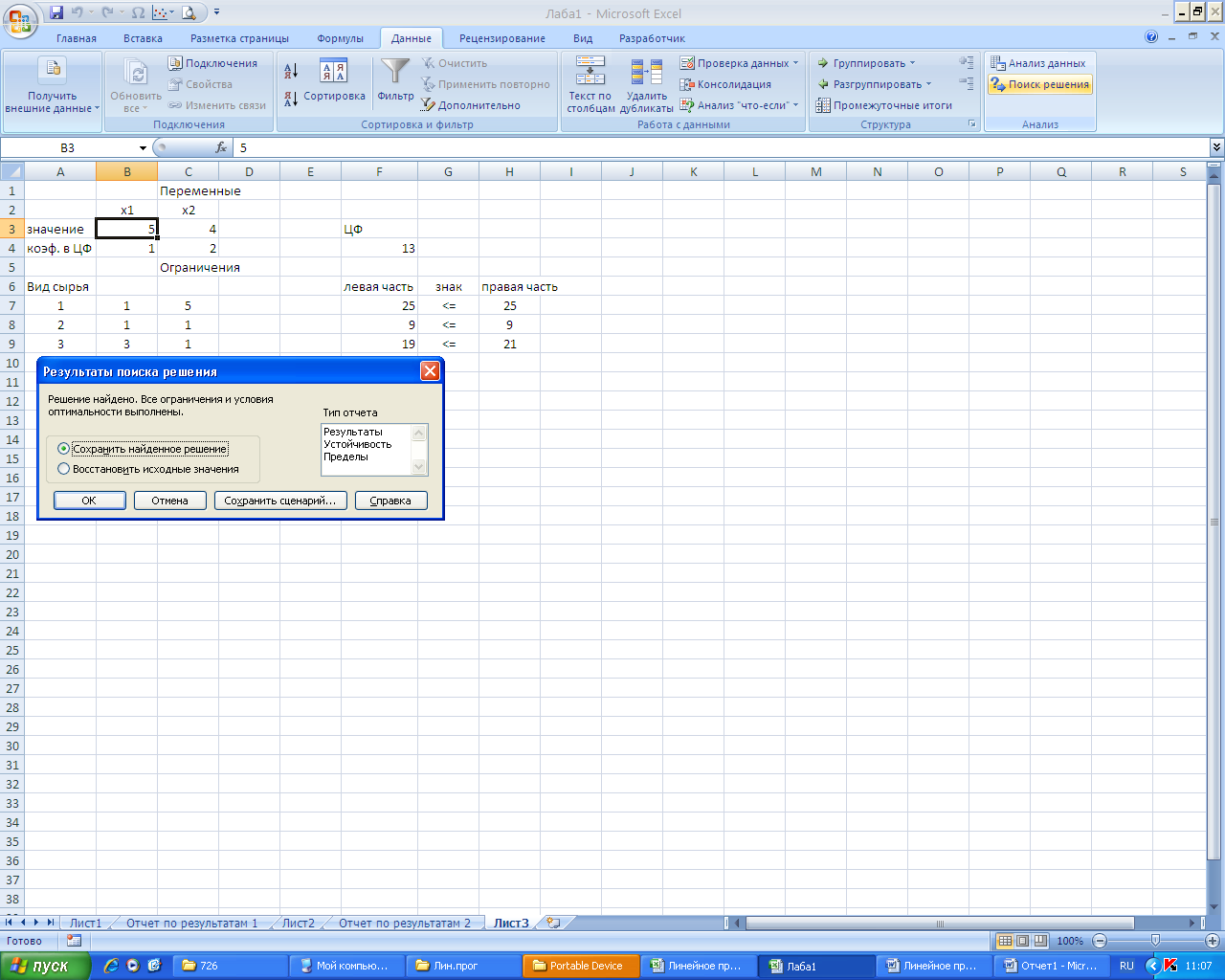
Рисунок 4 – Найденное решение
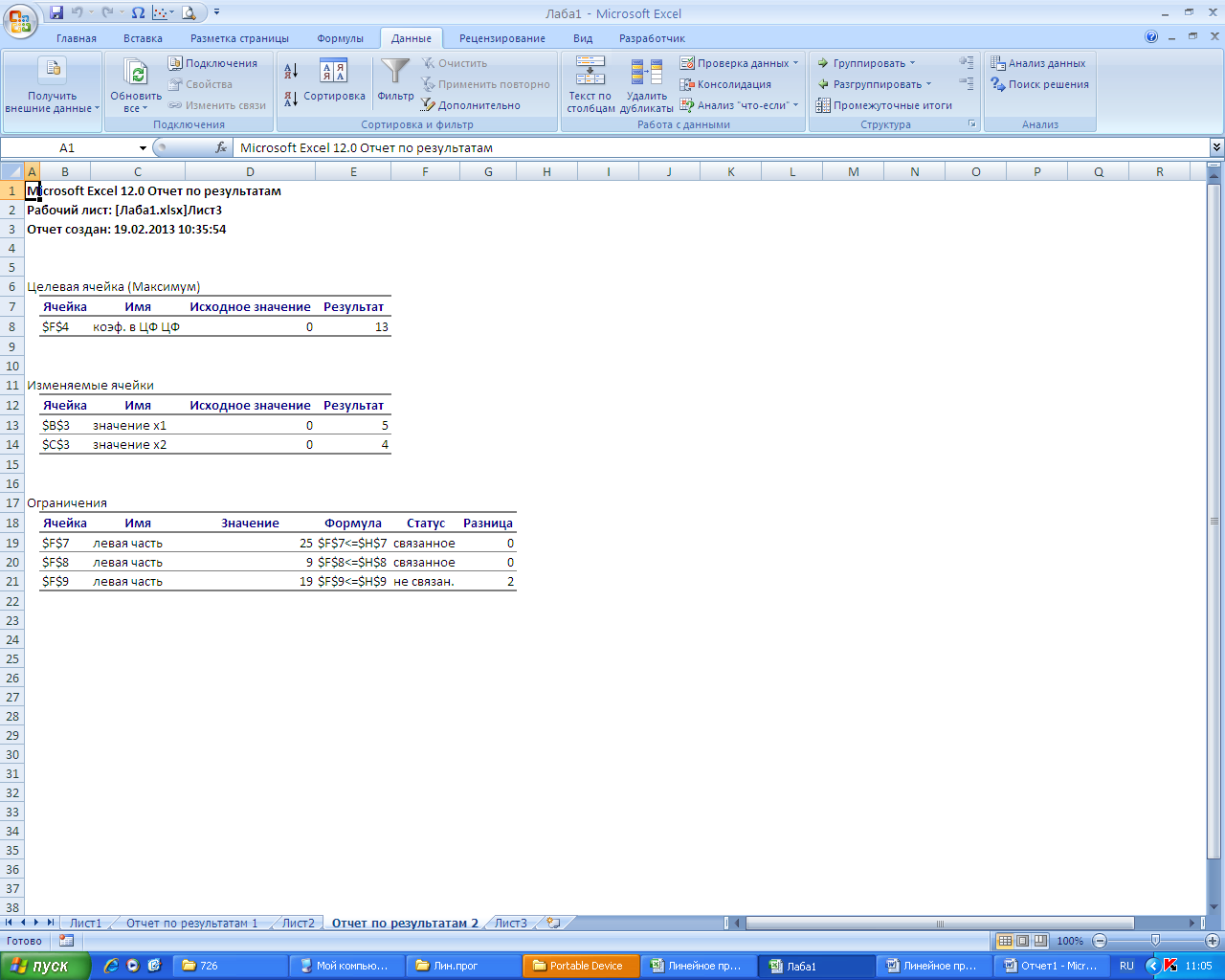
Рисунок 5 – Отчет по результатам
Результат: максимальная прибыль, полученная предприятием при реализации продукции составит 13 ден. ед. При этом будут выпущены 5 единиц продукции П1 и 4 единицы продукции П2.
Ответы на контрольные вопросы.
Дайте определение линейного программирования.
Наука о методах исследования и отыскивания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения.
Что называется математической моделью экономической задачи и как она строится?
Математической моделью экономической задачи называется модель, характеризующая сущность данной задачи, в данной модели учитываются характерные особенности задачи, а также ограничивающие условия, влияющие на результат.
Какие виды ограничения могут содержаться в задаче линейного программирования?
ЗЛП, как правило, содержит линейные ограничения, а именно системы уравнений и неравенств, которым удовлетворяют переменные задачи.
Как перейти от неравенств к уравнениям?
Для перехода от системы неравенств к системе уравнений, в левую часть каждого неравенства добавляем по одной неотрицательной переменной, в зависимости от знака неравенства либо с «+» для ≤ , либо с «-»для ≥ , а знак неравенства заменяем на знак равно.
Какие переменные называют дополнительными и какой коэффициент в линейной функции задачи линейного программирования?
Переменные с нулевым коэффициентом, входящие в целевую функцию после перехода в процессе решения от неравенств к равенствам.
