Лекция 6.

Зубчатые передачи Принцип действия и классификация

Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес (рис.6.1, где а – внешнее; б – внутреннее зацепление, в – реечная передача).

По расположению осей валов различают: передачи с параллельными осямии с цилиндрическими зубчатыми колесами внешнего или внутреннего зацепления (см.рис 6.1); передачис пересекающимися осями(конические зубчатые колеса, см.рис. ); передачис пересекающимися осями– цилиндрические винтовые (см.рис. ), конические гипоидные (см.рис. ), червячные (см.рис. ). Кроме того, применяют передачи между зубчатым колесом и рейкой (см.рис.6.1,в). Эти передачи являются частным случаем передачи с цилиндрическими колесами, у которой диаметр одного из колес равен бесконечности. Они служат для преобразования вращательного движения в поступательное, и наоборот.

По расположению зубьев на колесах различают: прямозубые– (см.рис.6.1),косозубые (см.рис.6.4) передачи и передачис круговым зубом(см.рис. ).

По форме профиля зуба различают:эвольвентныеикруговыепередачи. Наиболее распространен эвольвентный профиль зуба, предложенный Эйлером в 1760 году. Он обладает целым рядом существенных, технологических и эксплутационных преимуществ. Круговой профиль зуба предложен М.Л.Новиковым в 1954 году. По сравнению с эвольвентным он позволяет повысить нагрузочную способность зубчатых передач.

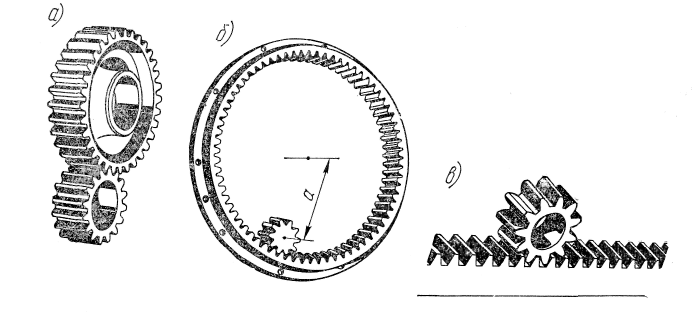
Рис.6.1

Оценка и применение

Основные преимущества зубчатых передач: а) высокая нагрузочная способностьи, как следствие, малые габариты (рис.6.2, где а – зубчатая, б – ременная, в – клиноременная, г – цепная передачи с одинаковыми характеристиками);

б) большая долговечность и надежность работы(большинство зубчатых передач

Рис.6.2

имеет практически неограниченный срок службы; в) высокий к.п.д.(до 0,970,98 в одной ступени); г) постоянство передаточного отношения(отсутствие проскальзывания); д) возможность применения в

широком диапазоне скоростей(до 150 м/с),мощностей(до десятков тысяч кВт) ипередаточных отношений(до нескольких сот).

Среди недостатков зубчатых передач можно отметить повышенные требования к точности изготовления, шум при больших скоростях, высокую жесткость, не позволяющую компенсировать динамические нагрузки.

Краткие сведения о геометрии и кинематике

Основные параметры Меньшее из пары зубчатых колес называют шестерней, а большее –колесом. Терминзубчатое колесоявляется общим. Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2 (рис.6.3). Кроме того, различают индексы, относящиеся: - к начальной поверхности или окружности;b– к основной поверхности или окружности;a– к поверхности или окружности вершин и головок зубьев;

Рис.6.3

f– к поверхности или окружности впадин и ножек зубьев.

Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.

z₁иz₂– число зубьев шестерни и колеса;u=z₂/z₁– передаточное число (отношение большого числа зубьев к меньшему – используется наряду с передаточным отношениемi=n₁/n₂, как удобное при расчете на контактную прочность);p– окружной шаг по делительной окружности (равный шагу исходной зубчатой рейки); р_b= рcos- окружной шаг по основной окружности;- угол профиля делительный (равный углу профиля исходного контура по ГОСТ 13755-68= 20⁰);_- угол зацепления или угол профиля начальный

;

m= р/- окружной модуль зубьев (является основной характеристикой размеров зубьев). Значения модулей стандартизированы в диапазоне от 0,05 до 100 мм.

D=pz/=mz– диаметр делительной окружности (по которой обкатывается инструмент при нарезании);d_b=dcos- диаметр основной окружности (разверткой которой являются эвольвенты зубьев);d_1иd_2– диаметры начальных окружностей (по которым пара зубчатых колес обкатывается в процессе вращения);

.

У передач без смещения и при суммарном смещении х_ = 0 (см.ниже) начальные и делительные окружности совпадают:

.

При нарезании колес со смещением делительная плоскость рейки (делительная окружность инструмента) смещается к центру или от центра заготовки на величину хm(см.рис.6. ); х – коэффициент смещения исходного контура. Смещение от центра считается положительным (х > 0), а к центру – отрицательным (х < 0).

где

у – коэффициент уравнительного смещения при х_  0 (определяется по ГОСТ 16532-70 или [ ].

Для передач без смещения и при х₁ = х₂ или х_ = 0

у = 0; _ =  = m(z₁ + z₂) / 2.

h = m(2h*_ +c* - у) – высота зуба;

d_ = d + 2m(h*_ +x - у) – диаметр вершин зубьев;

d_f = d - 2m(h*_ + c* - x) – диаметр впадин;

h*_ - коэффициент высоты головки зуба (по ГОСТ 13755-68 h*_ = 1);

с* - коэффициент радиального зазора (по ГОСТ 13755-68 с* = 0,25).

Для колес без смещения h = 2,25 m; d_ = d + 2m; d_f = d – 2,5m.

А₁А₂ – линия зацепления (общая касательная к основным окружностям); g_ - длина активной линии зацепления (отсекаемая окружностями вершин зубьев); П – полюс зацепления (точка касания начальных окружностей и одновременно точка пересечения линии центров колес О₁О₂ с линией зацепления).