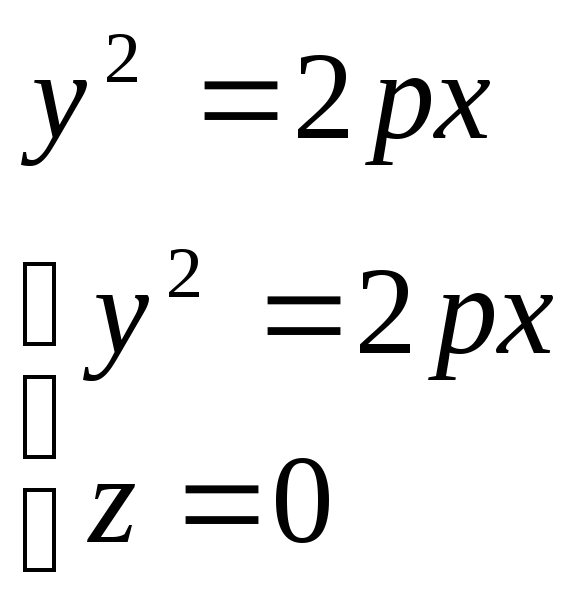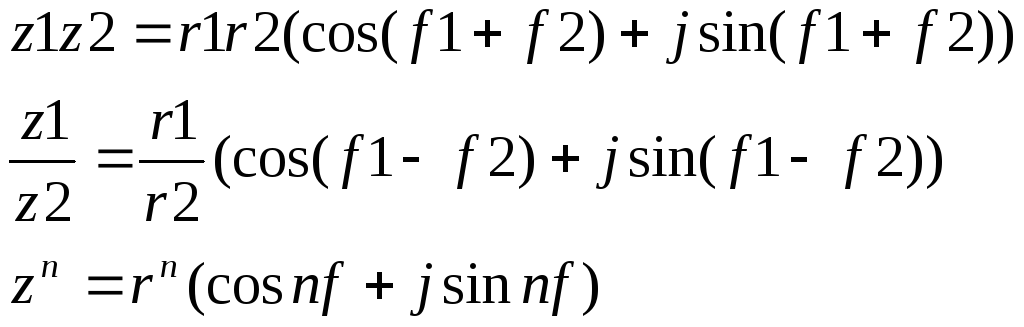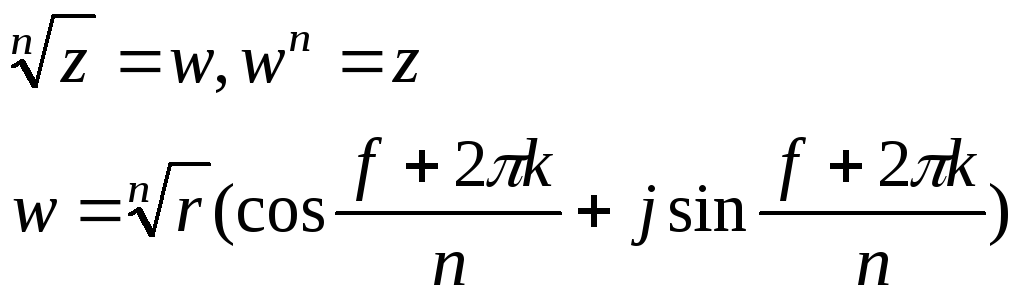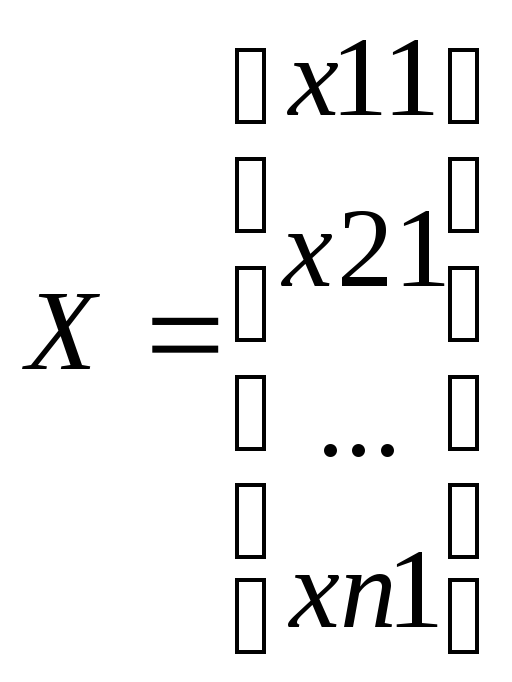Lineynaya_algebra
.doc|
№1 Понятие множества является основным в математике. Это понятие не определяется через другие. Обознач A, B,C, а элементы множества – а, в, с. АсВ – А содержится в В. А=В – кажд элемент множества А является элем множества В. Ø – пустое множество. Для обозначения множеств используют фигурн скобки. Объединением множества А и В называется множество состоящее как из элементов множества А так и В. U – объединение. AuA=A. Au Ø=A. ∩ - пересечение. A∩A=A. Au Ø= Ø. 1) AUB=BUA . A∩B=B∩A 2) AU(BUC)=(AUB)UC 3) AU(B∩C)=(AUB)∩(AUC) 4) AUØ=A 6) AUA=A Разность А и В – это множество А\В состоящее из элем множества А которых нет в В.
№4
где е- иррациональное число.
№7 Определителем матрицы 1-го порядка А=(а11) является единственный элемент этой матрицы. Определителем 2-го порядка называется число, характеризующее матрицу 2-го порядка, которое находится по следующему правилу: из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А. Определителем матрицы 3-го порядка это число равное сумме произведений элементов любой строки (столбца) на алгебраические дополнения элементов этой строки ((-1)ikAik). 1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то | | этой матрицы равен 0. 2)При транспонировании матрицы её определитель неизменяется. 3) При перестановке местами 2-х строк или столбцов матрицы её определитель меняет свой знак на противоположный. 4) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0. 5)Если 2 строки или 2 столбца матрицы пропорциональны, то её | | равен 0. 6) Определитель матрицы не изменяется если к элементам одной строки или столбца прибавить элементы другой строки или столбца, умноженный на одно и то же число.
№11
предполагая, что
а11 и прибавляем ко второму и т.д. Получим Ур-ия не содержащие х1. Аналогично со вторым.
(2)- имеет единственное решение. (3)- имеет бесконечно много решений. Одни неизвестные выражаются через другие. (4)- не имеет решений.
№14 Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора одинаковые, когда они имеют одинаковое направление и равные модули. Противоположные, когда имеют равные модули и противоположное направление. Нуль-вектор. Единичный вектор. 1.умножение на число: произведение вектора А на число наз. такой вектор В, который обладает след. св-ми: а) |А|=|| |А| б) >0, то А, <0, то А. 2.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 3. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а. 1) a+b=b+a 2) (a+b)+c = a+(b+c) 3) a+0=a 4) a+(-a)=0
№22 Скалярное произведение 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. Обозначается (а,в) ; а*в=|а|*|в|*cos; а*в=|а|прва
Если a (x y z); b (X Y Z), то ab= xX+yY+zZ Приложение. 1 проекция вектора на ось. Прab=ab/|a| 2 Угол между векторами cos f = ab/|a||b| 3 работа силы A=FS №24 Смешанным произведением векторов a,b,c наз. векторно-скалярное произведение, являющееся числом от векторного произведения ab скалярно на с. (abc)=[ab]c 1 a,b,c комплонарны т. и т.т. когда их произведение = 0. 2 операции скалярного и векторного произведения можно менять местами. 3 круговая перестановка его множителей не меняет знак, а перестановка двух соседних – меняет. a*b*c=-b*c*a a*b*c=c*a*b=b*c*a
Если
a=(x y z); b=(X Y Z); c=(Q W E), то
abc=
1 Объем параллепипеда V= +-abc 2 Объем пирамиды V= +- 1/6abc
№26 Ур-ие плоскости заданной точкой М0(x0 y0 z0) и нормальным вектором n(A B C) 1 n= (r-r0) – векторное ур-ие плоскости. 2 A(x-x0)+B(y-y0)+С(z-z0)=0 - общее Ур-ие. Частный случай: Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0) Если A=0, то By+Сz+D=0 Если B=0, то Ax +Сz+D=0 Если C=0, то Ax+By+D=0 Если A=B=0, то Сz+D=0 Если A=C=0, то By+D=0 Если A=D=0, то By+Сz=0 Если B=D=0, то Ay+Сz=0 3 ур-ие плоскости в отрезках x/a+y/b+z/c=1 4 нормальное Ур-ие плоскости
5 ур-ие плоскости проходящей через 3 точки
№29 Кривые 2го порядка описываются с помощью общего ур-ия: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где а) Каноническое ур-ие эллипса Эллипс – это множество точек плоскости сумма расстояний от которых до двух данных точек F1, F2 есть величина постоянная, большая чем расстояние между ними. Эксцентриситет эллипса- это отношение фокусного расстояния к длинне большей оси
Если a=b, то x2+b2=a2 - ур-ие окружности. б) Ур-е гиперболы: x2/a2-y2/b2=1 гипербола- это множество точек плоскости, разность расстояний от которых до f1 и f2, взятая по модулю, есть величина постоянная.
в) ур-е параболы: y2=2px или y=ax2 парабола- это множество точек плоскости равноудаленных от данной точки (фокуса) до данной прямой (директрисы). г) ур-е эллипса: x2/a2-y2/b2+z2/c2=1
№32 относительно декартовой системы координат на плоскость общее Ур-ие второго порядка Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где A,B,C,D,E,F – числа, задает одну из линий эллипса (окружности) или случай их выраждения (пары прямых, мнимый эллипс, мнимую окружность) Случай когда Ур-ие второго порядка не содержит слагаемого с поизведением XY то Ур-ие может быть упращено.
№35 Эллипсоид вращения — это поверхность, образованная при вращении эллипса вокруг одной из его главных осей. b – большая полуось, с – малая.
OYZ
|
№2 Запись комплексного числа в виде x+jy называется алгебраической формой. Сумма комплексных чисел равна суммам действительных и мнимых частей.
При умножении
Деление
При умножении на сопряженное получится x2+y2
№5 Матрицей размера mxn называется таблица состоящая из mn множества М и содержащая m строк и n столбцов. Элементы множества М называются элементами матрицы. Матрицы обозначаются A,B,C. Элементы матрицы – aik. [], ( ), || ||, [aik]mn . матрицы равны если они одинаковых размеров. Матрицей строкой называют матрицу, состоящую из одной строки. Матрицей столбцом - из одного столбца. Матрица, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-ого порядка. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нулевой. 1)Умножение матрицы на число. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы. 2)Сложение 2-х матриц: условие - складывать можно только матрицы одинакового размера. Суммой 2-х матриц А и В называется матрица С=А+В. Для того, чтобы сложить 2 матрицы, необходимо складывать между собой элементы, стоящие на одинаковых местах. 3)Вычитание 2-х матриц: операция аналогична сложению. 4)Умножение 2-х матриц: умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mk на матрицу В размера kn называется матрица С размера mn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В. 5)Транспонирование. транспонирование-операция, в результате которой строчки и столбцы матрицы меняются местами.
№8 матрица обратная квадратной матрице А – это квадратная матрица В удовлетворяющая равенству АВ=ВА. Обратная матрица существует только для квадратной и имеет тот же порядок. Обозначается А-1. АА-1=А-1А=Е
№12 Рангом матрицы А называется наивысший порядок отличных от 0 миноров этой матрицы rang A=r(A). минор порядка S – это минор стоящий на пересечении любых S строк и S столбцов. Ранг матрицы заключен в 1<=r(A)<=min(m,n). r(A)=0 только когда матрица нулевая. При нахождении ранга можно пользоваться свойствами определителей. Ранг матрицы не изменяется при проведении элементарных преобразований. Преобразования: 1)отбрасывание строки или столбца, состоящих из одних нулей; 2)умножение всех эл-ов к.-л. строки или столбца матрицы на одно и то же число, отличное от 0; 3)изменение порядка строк или столбцов матрицы; 4)прибавление к каждому эл-ту к.-л. строки или столбца эл-ов др. строки или столбца, умноженных на одно и то же число, не равное 0; 5) транспонирование матрицы. Теорема Кронекера-Капелли: система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы совместной системы меньше неизвестных, то множество ее решений бесконечно.
№15 линейные пространства являются одним из основных и возникают в результате обобщения векторов, матриц, действительных чисел и т.д. V={x,y,z} Операция сложения z= x+y, z, x, y принадлежат V Операция умножения z=x, z, x, принадлежат V Действительным линейным пространством называется множество V в котором определены сложение элементов и умножение их на действительные числа, удовлетворяющие следующим аксиомам:
1
2
3
4
5
6
7
8
Элементы действительных линейных пространств называются векторами. Примеры: 1 Множества всех свободных векторов 2 матрицы mn
№23
левая ----- правая Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. |c|=|a|*|b|*sin. 2. ca и cb. 3. тройка а,в,с-правая. Если один из векторов нулевой то произведение этих векторов = 0.
ab = 0 т. и т.т., когда один из векторов =0 или они перпендикулярны.
Если a
(x
y
z);
b
(X
Y
Z),
то
1 площадь параллелограмма S=|ab| 2 площадь треугольника S=1/2|ab|
№27 1 параметрическое Ур-ие. r=r0+tS, где r(x y z); r0(x0 y0 z0), t – параметр.
2 Каноническое уравнение прямой
3 Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
4 Общее Ур-ие прямой
№30 Директрисы эллипса (гиперболы) – это две прямые перпендикулярные большей оси эллипса (действительной оси гиперболы) и расположенные симметрично относительно центра на расстоянии а/E от него. Основное свойство директрис: отношение расстояния R произвольной точке до фокуса к расстоянию d этой точки до соответствующей директрисы есть постоянная величина R/d=E.
№33 цилиндрическая поверхность – это поверхность описываемая прямой (образующей), движущейся вдоль некоторой линии и остающейся || некоторой прямой. Цилиндр второго порядка – это цилиндрическая поверхность, направляющей которого является эллипс, окружность или парабола. уравнение - x2/a2-y2/b2=1
эллиптический
цилиндр
гиперболический
цилиндр
параболический
цилиндр
№36
Если вмести с гиперболой вращать асимптоты, то они опишут конус – асимптотический конус гиперболоида вращения. Прямолинейные образующие – образующие, которые лежат всеми точками на гиперболоиде. Двуполостный гиперболоид – это поверхность, образованная вращением гиперболы вокруг действительной оси.
|
№3 r – длинна |OM| f – угол между |OM| и положительным направлением OX r и f – полярные координаты. x=rcosf y=rsinf
при r=1
№6 a11x1+a12x2+…+a1nxn=b1, где a1n называются коэффициентами при неизвестных, а b- свободным коэффициентом. Два линейных ур-я называются равносильными, если есть общее решения. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система ур-ий называется определённой, если она имеет одно единственное решение, и неопределённой, если решений множество. Матрица, эл-тами которой являются коэффициенты при неизвестных системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных коэффициентов, называется расширенной матрицей.
№10
|А|= A-1=1/|A| и умнож на определитель, составленный из обратную матрицу.
№13 пусть дана система (1). Базисным минором матрицы называется отличный от нуля минор порядок которого равен рангу этой матрицы. Базисными неизвестными совместной системы называются r- неизвестных, коэффициенты которых образуют базисный минор. Остальные неизвестные называются свободными. 1) находим ранг основной матрицы и ранг расширенной. Если они неравны, то система несовместна. 2) Если они равны, то система совместна и выделяют базисный минор и базисные неизвестные. Исходную систему заменяют эквивалентной. 3) Если число базисных неизвестных равно числу неизвестных, то система имеет единственное решение (находится по формулам Крамера). Если число базисных неизвестных меньше числу неизвестных, то базисные неизвестные находят через свободные.
№16 Рассмотрим алименты x1, x2, xn (1) линейного пространства V. y=1x1+2x2+…+nxn, принадлежит R. Система векторов (1) линейно зависима, если 1x1+2x2+…+nxn = 0, при этом хотя бы одно не равно нулю. Система векторов (1) линейно независимой, если 1x1+2x2+…+nxn = 0, при всех = 0. Если система векторов линейно зависима, то хотя бы одно выражается через остальные. 1 Всякая система векторов, имеющая нулевой вектор – линейно зависима. 2 Если К векторов (К<n) системы (1) линейно зависима, то и система (1) линейно зависима. 3 Если из системы линейно независимых векторов отбросить r векторов (r<n), то оставшаяся система линейно независима. 4 Если среди векторов системы (1) имеются такие xk и xn, что xk=xn, то система линейно зависима. 5 Векторы x1+x2+…+xn линейно зависимы т. и т.т., когда один из векторов является линейной комбинацией остальных. Пусть n – натуральное число. Линейное пространство V называется n-мерным, если в нем существуют n линейно независимых векторов, а всякие (n+1) линейно зависимы. n-называется размерность линейного пространства. обозначается dimV. Если пространство нулевое, то его размерность = 0. обозначается dimV. Базисом n- мерного пространства называется любая упорядоченная система n-линейно независимых векторов.
№25 Уравнение линии на плоскости относительно выбранной системы координат – это такое уравнение с двумя переменными, которому удовлетворяют x,y в любой точке данной линии и не удовлетворяют координаты не одной точки, не лежащей на линии. Пусть 0 (0,0)-центр окружности.
r2=(x-x0)2+(y-y0)2- ур-е окружности а=b=0, то x2+y2=r2 1 A(x-x0)+B(y-y0)=0 2 общее Ур-ие прямой на плоскости. Ax+By+C=0 3 величине отрезка, отсекаемого на оси OY. y=kx+b 4 ур-ие прямой по двум точкам. (x-x1)/(x2-x1)=(y-y1)/(y2-y1) 5 ур- ие прямой по угловому коэффициенту и точке y-y0=k(x-x0) 6 параметрическое ур- ие прямой x=x1+t(x2-x1) y=y1+t(y2-y1) 7 ур- ие прямой в отрезках по осям x/a+y/b=1 Угол второй прямой к первой – это угол на который нужно повернуть первую, чтобы она совпала со второй
№28 Угол между прямыми называется любой из двух углов образованных прямыми проведенными через одну точку в пространстве и || данным прямым. Для определения угла следует найти угол между направляющими векторами этих прямых.
S1 | S2 S1 || S2
Угол между прямой и плоскостью- это угол, образованный прямой и ее проекцией на плоскость.
Угол между плоскостями.
A1A2+B1B2+C1C2=0 | A1/A2=B1/B2=C1/C2 ||
№31 Пусть дана декартова система координат.
X=a-x Y=y-c - выражение новых координат через старые. Z=z-c
x=a+X y=b+y - выражение старых координат через новые. z=c+Z
Если система на плоскости, то используется две координата.
№34 Коническая поверхность (конус) – это поверхность образованная движением прямой, проходящей через данную точку (вершину) и скользящую по данной кривой. x2/a2+y2/b2+z2/c2=0 – кононическое Ур-ие второго порядка.
Поверхность вращения. Вращением фигуры F вокруг данной прямой (оси) называется такое движение при котором каждая точка F описывает окружность в плоскости пенпердикулярной оси вращения и центром на оси вращения.
Правело получения
оси вращения. Чтобы получить Ур-ие
поверхности вращения в плоскости OYZ
вокруг оси OZ
нужно в Ур-ии этой линии y
заменить на
Знак должен совпадать со знаком у на исходной кривой.
№37 Параболоид вращения – это поверхность, образованная вращением вокруг оси. x2+y2=2pz - уравнение параболоида вращения вокруг OZ
|


 (1)
(1)
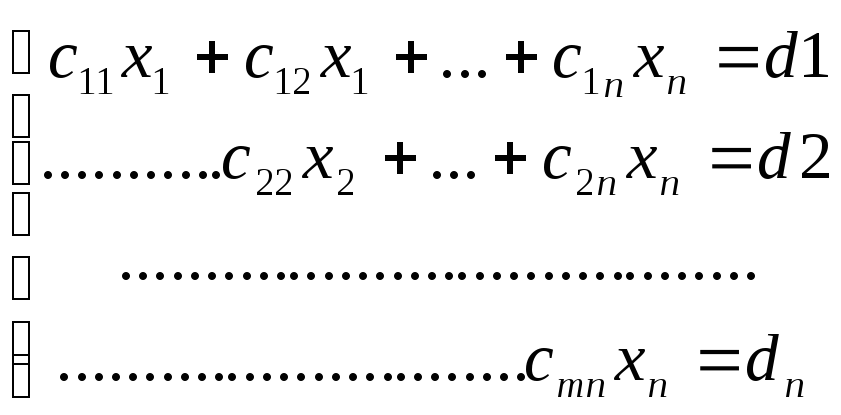 (2)
(2)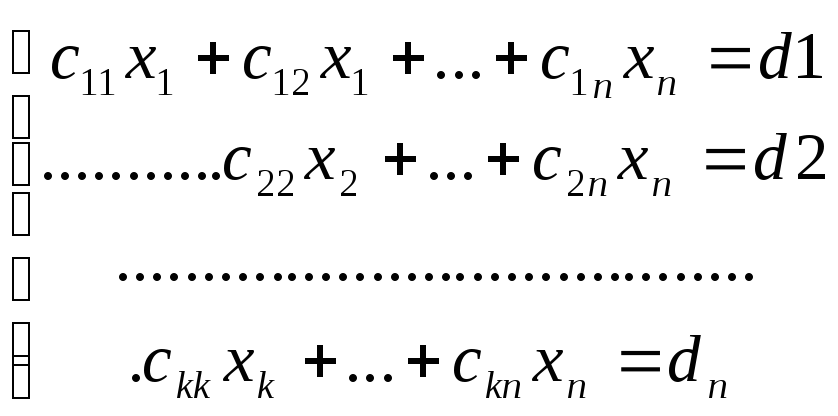 (3)
(3)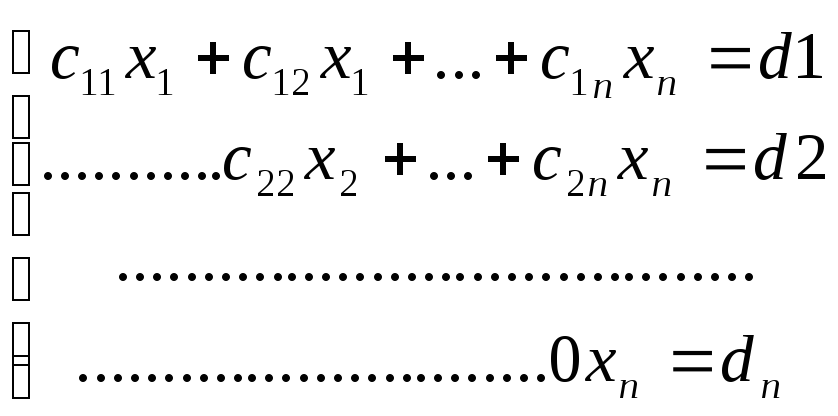 (3)
(3)

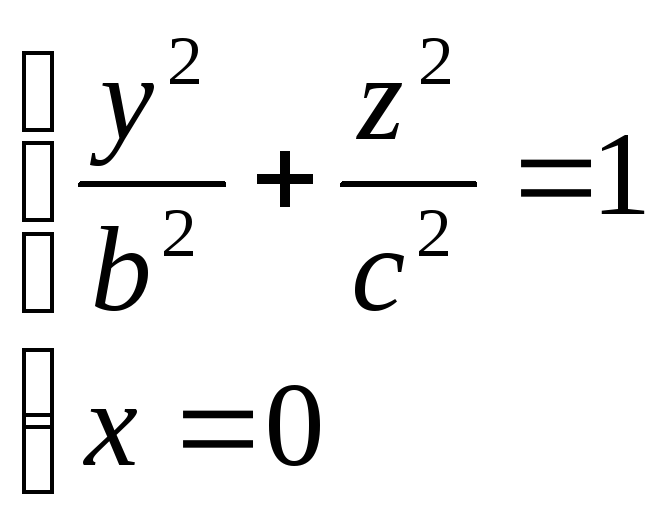

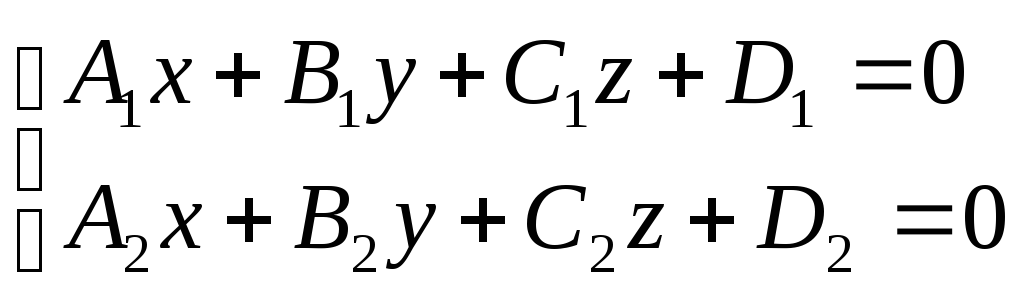


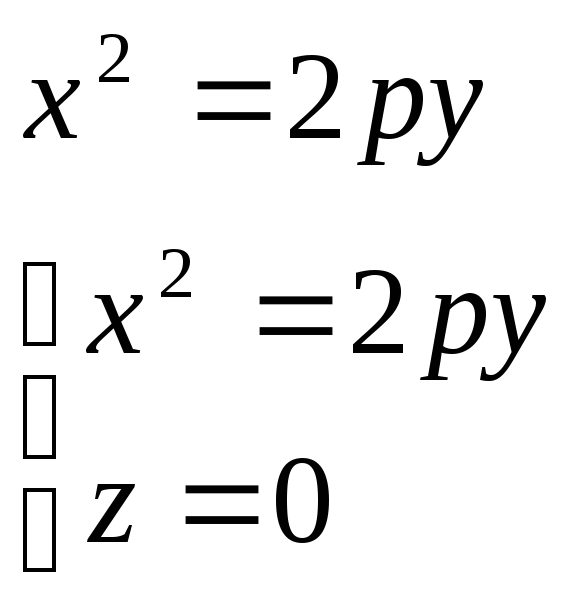 или
или