1.4. Условия непрерывности потока в сети
Определим на сети два особых узла. Узел А назовем пунктом отправления или источником, а пункт В – пунктом назначения или стоком. Все остальные узлы будем называть промежуточными или транзитными.
Далее определим транспортный поток как множество неотрицательных действительных чисел, удовлетворяющих следующему соотношению:
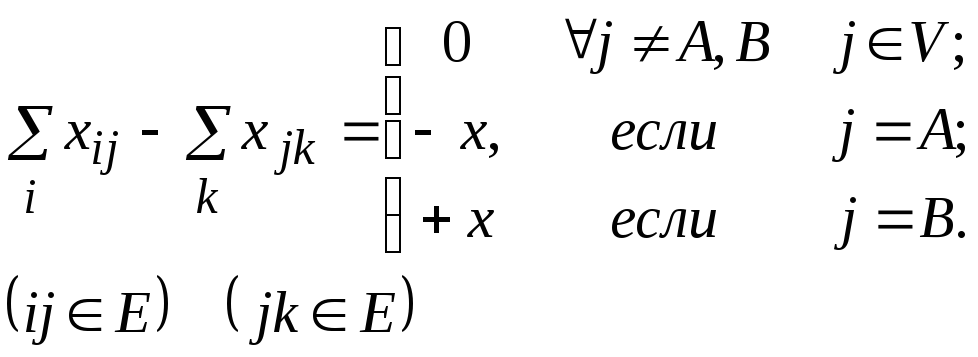
Это соотношение говорит о том, что чистый поток равен нулю для каждого узла сети, кроме пункта отправления и пункта назначения. Поэтому данное соотношение носит название условий непрерывности потока в сети.
Эти условия необходимо понимать следующим образом (Рисунок 15).
Рисунок 15 – К определению условий непрерывности потока в сети
Левая сумма
– это сумма потоков, стекающихся вj-й
узел; правая сумма
– сумма потоков, истекающих изj-го
узла.
Проиллюстрируем условия непрерывности потока в сети на примере (Рисунок 16).
Пример.
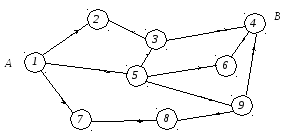
Рассмотрим узел
5
(то есть
).
Предполагая, что движение происходит
в направлении, указанном на дугах
стрелками, для узла5
получим
.
Таким образом, чистый поток в узле 5 равен нулю: сколько транспортных единиц приходит в узел 5, столько же из него выбывает.
Тогда для точки истока А получим:
.
Аналогично для точки стока В получим:
.
Полученные соотношения имеют место только в том случае, если определены направлении движения по графу (определены маршруты перевозок). Если направления движения изменятся на противоположные, то в записанных выше условиях поменяются знаки.
Например, если в рассматриваемом выше примере изменить на противоположное направление движения по дуге (5, 3), то условие непрерывности потока в сети примет вид:
.
Записанные выше условия непрерывности потока в сети относились к так называемому однотерминальному потоку, то есть к потоку с единственным источником и единственным стоком.
На практике, как известно, при рассмотрении различных перевозочных процессов могут существовать многотерминальные потоки со многими источниками и многими стоками.
В этом случае условие непрерывности многотерминального потока в сети будет иметь следующий вид:
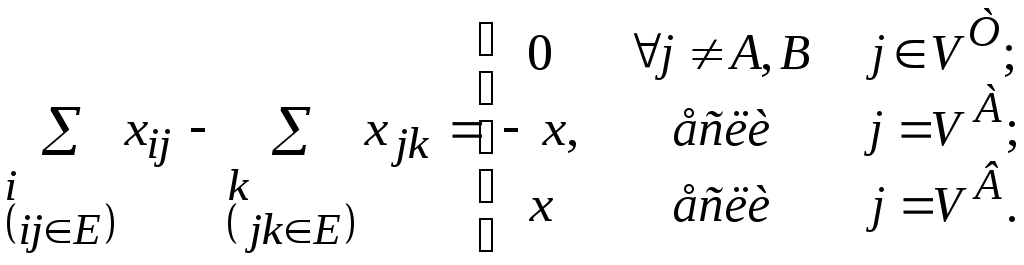
(1.2.9)
где 
– множество промежуточных узлов
(транзитных узлов);
–множество пунктов
отправления;
–множество пунктов
назначения.
Многотерминальный поток можно заменить на однотерминальный, связывая все источники в суперисточник, все пункты назначения в суперсток.
При этом предполагается, что суммарный поток берет начало в суперисточнике и заканчивается в суперстоке.
Все первоначальные источники и стоки становятся тогда промежуточными узлами.
Покажем это на примере.
Пример (Рисунок 16).
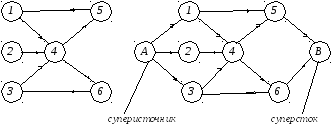
Рисунок 16 – Редукция многотерминального потока к однотерминальному
1.5. Основная транспортная задача
Сформулируем основную транспортную задачу, которая носит еще название стандартной транспортной задачи.
Пусть существует
множество источников, в которых
производятся товары
.
Кроме этого имеется множество стоков,
где потребляются товары
.
Между источниками и стоками имеются
связи
(Рисунок 17).
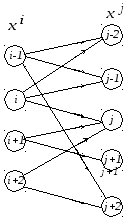
Рисунок 17 – К формулировке стандартной транспортной задачи
Для того, чтобы
перевезти единицу товара из i
в
j,
требуется заплатить
денежных единиц.
Задача теперь состоит в том, чтобы перевезти товары из пунктов производства в пункты потребления с минимальными затратами. Таким образом, необходимо минимизировать целевую функцию следующего вида
при условиях
;
.
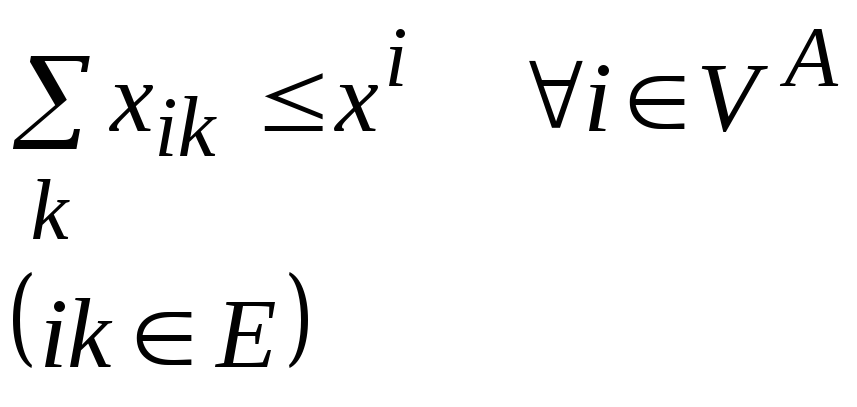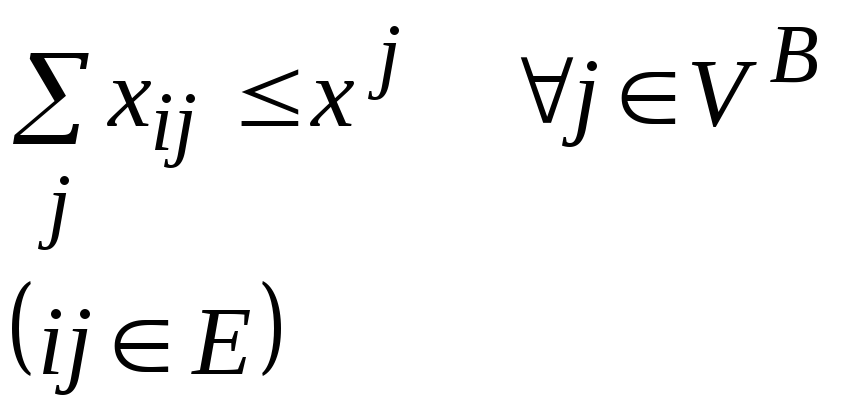Первое условие означает, что сумма вывозимых товаров по ik направлениям из источника i не должна превышать количество товара, произведенного в i-ом источнике.
Второе условие
показывает, что количество ввозимого
товара по ij
направлениям в j-й
сток может быть больше или равно
количеству потребляемых товаров. Если
,
то в стокахj
будут образовываться накопления товаров.
Таким образом, для того чтобы в транспортной задаче получилось допустимое решение, необходимо
.