
Matan
.docФормула Тейлора
1.
Разложить многочлен
![]() по степеням двучлена
по степеням двучлена
![]() двумя способами (с помощью формулы
Тейлора и без нее).
двумя способами (с помощью формулы
Тейлора и без нее).
2.
Разложить функцию
![]() по формуле Тейлора с остаточным членом
в форме Лагранжа при
по формуле Тейлора с остаточным членом
в форме Лагранжа при
![]() .
.
3. Разложить
функцию
![]() по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки
![]() .
.
4.
Записать пять первых членов формулы
Маклорена для функции
![]() .
.
Используя известные разложения для элементарных функций, записать формулы Маклорена для следующих функций.
5.
![]() . 6.
. 6.
![]() . 7.
. 7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
13.
.
13.
![]() .
.
14.
![]() . 15.
. 15.
![]() .
16.
.
16.
![]() .
.
17.
![]() . 18.
. 18.
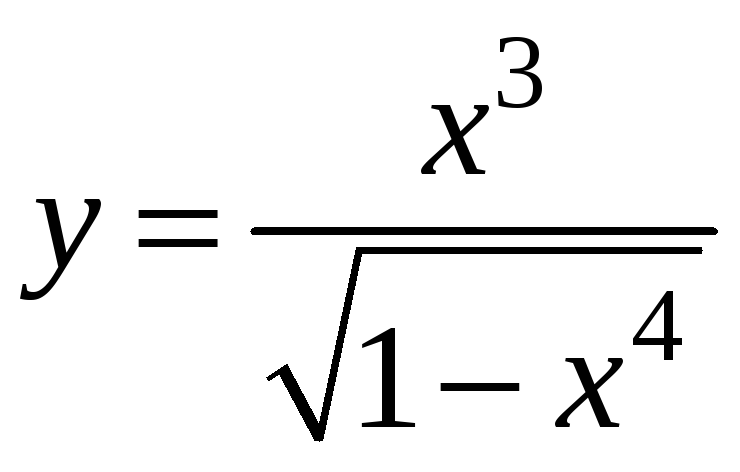 .
19.
.
19.
![]() .
.
Д.З. 1.
Разложить многочлен
![]() по степеням двучлена
по степеням двучлена
![]() двумя способами (с помощью формулы
Тейлора и без нее).
двумя способами (с помощью формулы
Тейлора и без нее).
2.
Разложить функцию
![]() по формуле Тейлора с остаточным членом
в форме Лагранжа при
по формуле Тейлора с остаточным членом
в форме Лагранжа при
![]() .
.
3.
Записать пять первых членов формулы
Маклорена для функции
![]() .
.
Используя известные разложения для элементарных функций, записать формулы Маклорена для следующих функций.
5.
![]() . 6.
. 6.
![]() . 7.
. 7.
![]() . 8.
. 8.
![]() .
.
9.
![]() .
10.
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() .
14.
.
14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
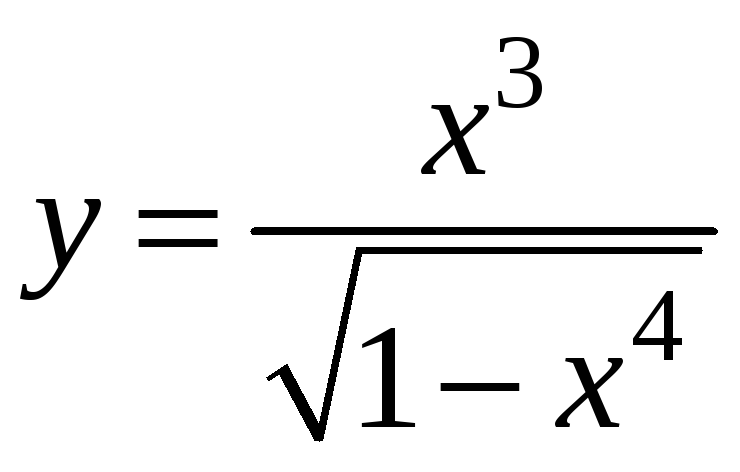 .
18.
.
18.
![]() .
.
Задания для самостоятельной работы 1
Разложить в ряд
Фурье следующие периодические функции
с периодом
![]() :
:
1.
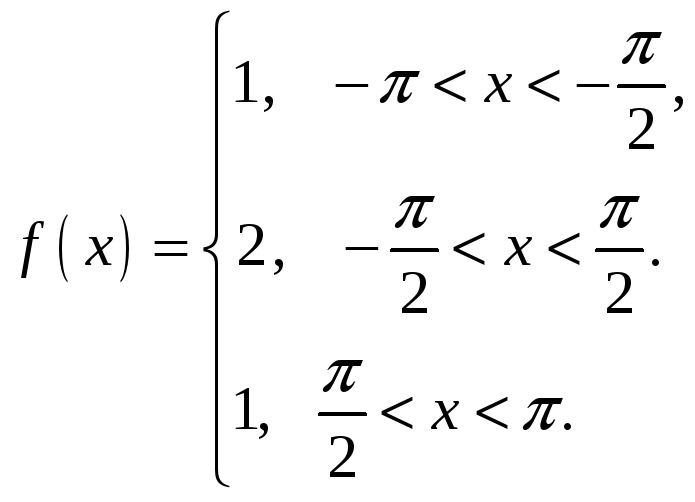 2.
2.
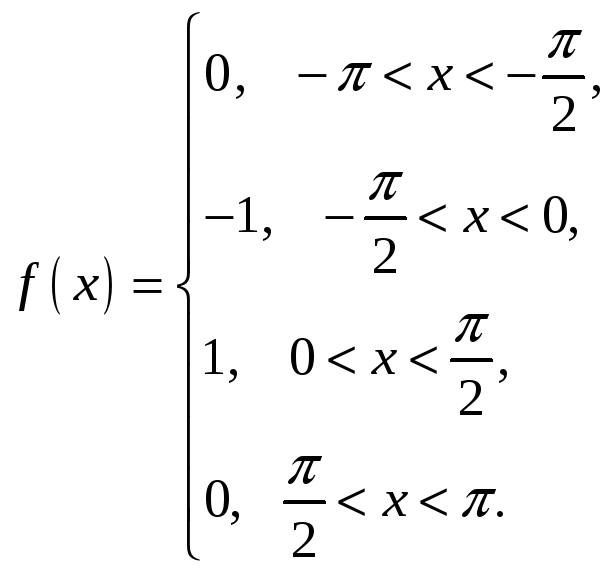 3.
3.
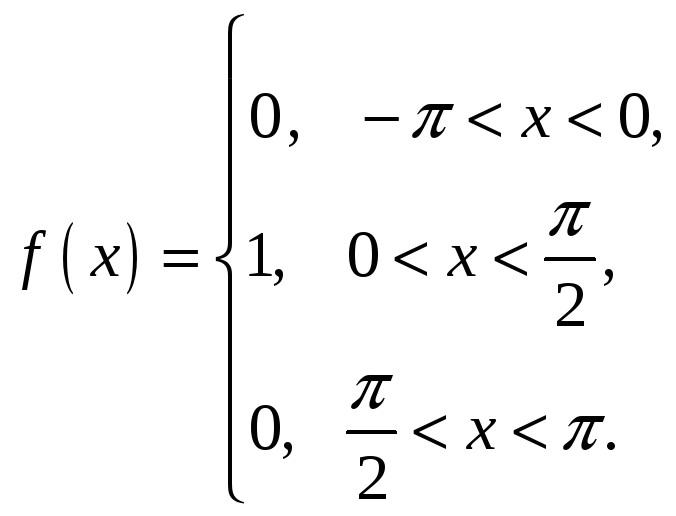
4.
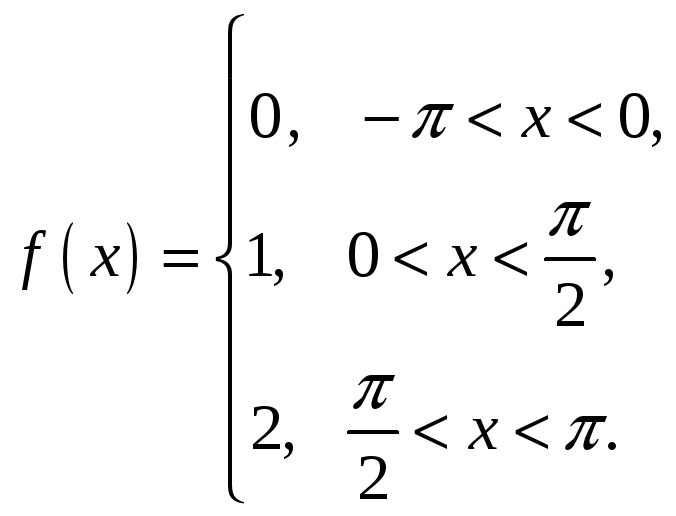 Ответы:
1.
Ответы:
1.
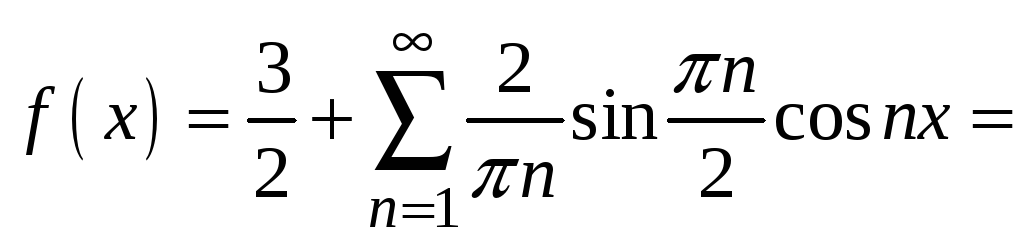
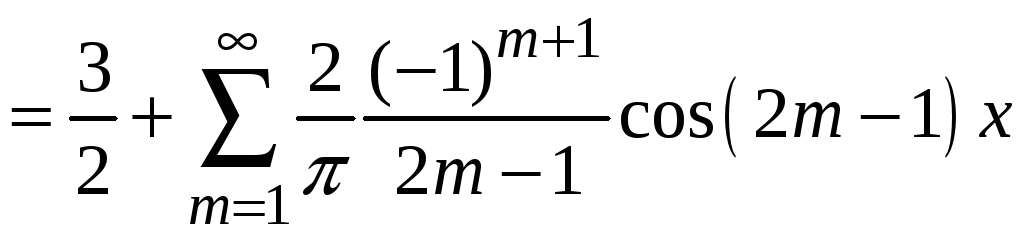 .
2.
.
2.
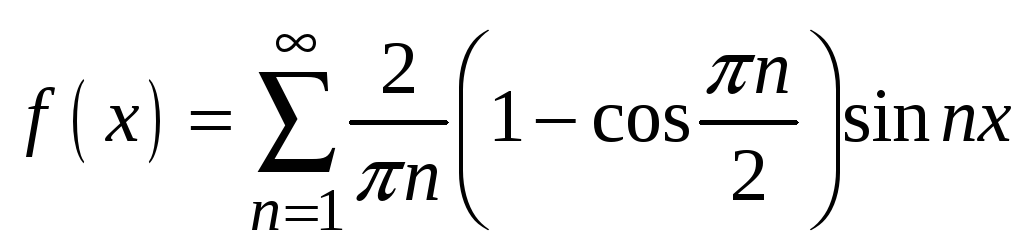 .
.
3.
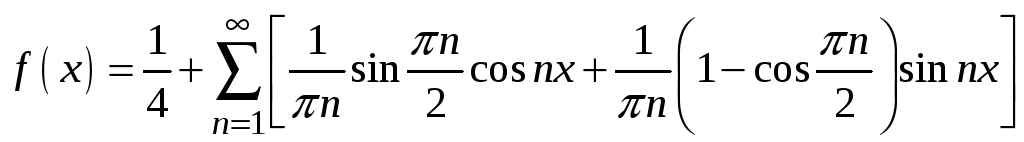 .
(см. на об)
.
(см. на об)
Задания для самостоятельной работы 2
1.
Разложить функцию
![]() в ряд Фурье на интервале
в ряд Фурье на интервале
![]() .
.
2.
Разложить функцию
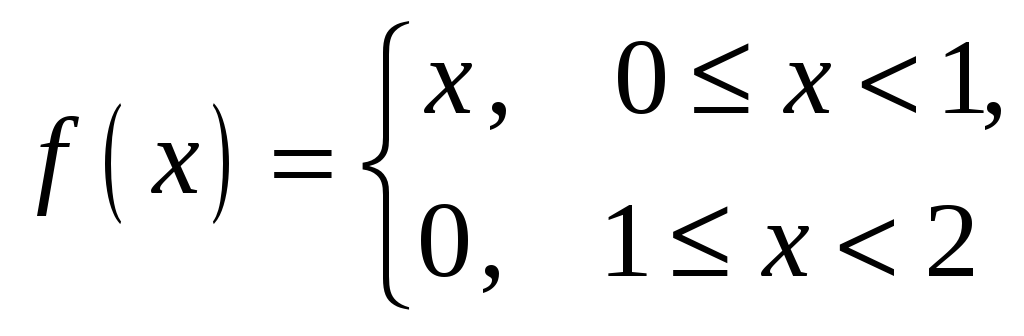 в ряд Фурье по синусам.
в ряд Фурье по синусам.
3. Разложить
функцию
![]() в ряд Фурье по косинусам на отрезке
в ряд Фурье по косинусам на отрезке
![]() .
.
4. Разложить
функцию
![]() в ряд Фурье на отрезке
в ряд Фурье на отрезке
![]() (сумма ряда имеет период, равный 2).
(сумма ряда имеет период, равный 2).
Ответы: 1.
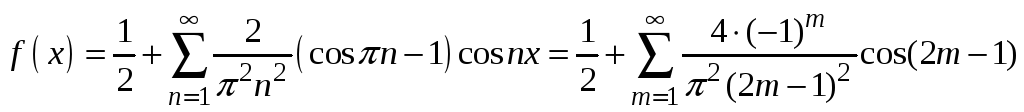 .
.
2.
 .
.
3.
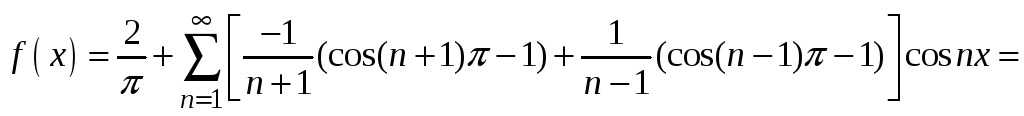
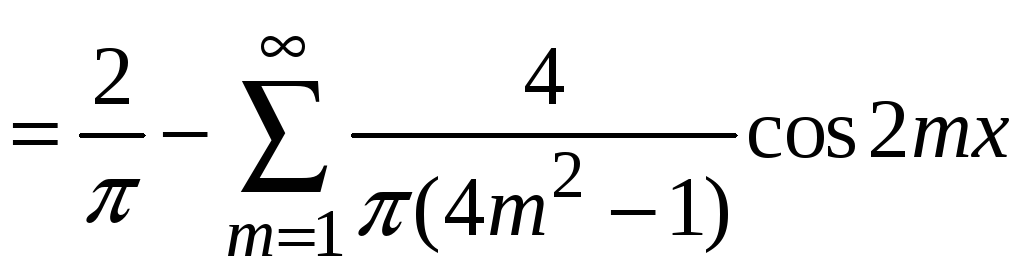 .
4.
.
4.
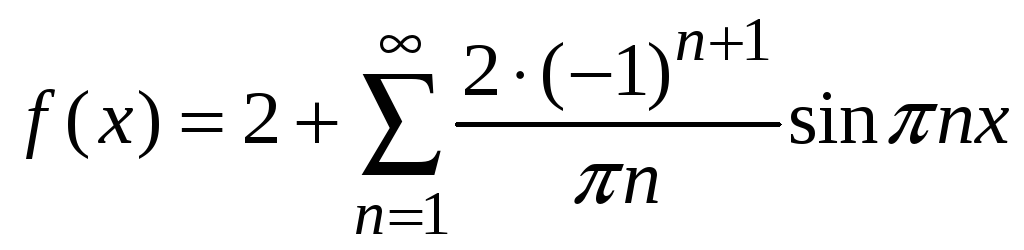 .
.
4.
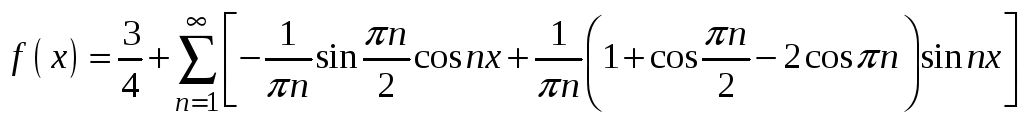 .
.
Числовые ряды (повторение)
Исследовать ряды на сходимость
1.
![]() .
. 2.
.
. 2.
![]() .
3.
.
3.
![]() .
.
4.
![]() . 5.
. 5.
![]() .
6.
.
6.
![]() .
.
7.
![]() . 8.
. 8.
![]() . 9.
. 9.
![]() .
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
![]() .
13.
.
13.
![]() .
.
14.
![]() 15.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() 18.
18.
![]() . 19.
. 19.
![]()
20.
![]() . 21.
. 21.
![]() .22.
.22.
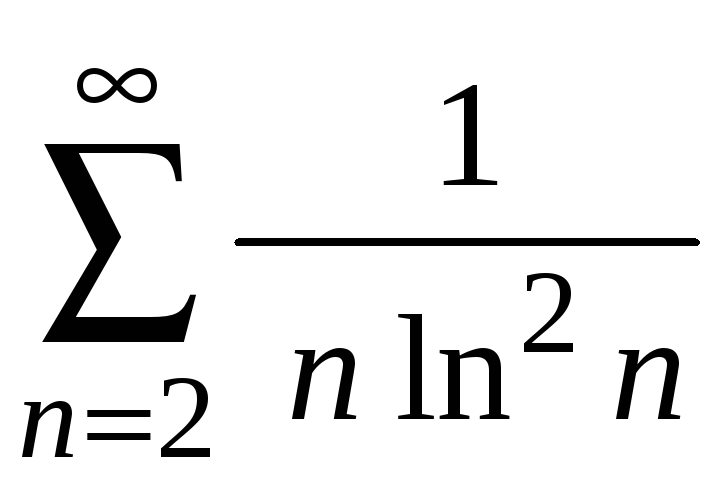 .
23.
.
23.
![]()
24.
![]() .
25.
.
25.
![]() .
26.
.
26.
![]() .
.
27.
![]() . 28.
. 28.
![]() .
29.
.
29.
![]() .
30.
.
30.
![]() .
.
31.
![]() 32.
32.
![]() .
.
Ряды
Д.З. Демидович, №№ 2417, 2418, 2420, 2421, 2423, 2425.
Д.З. Демидович, №№ 2427, 2429, 2438, 2439, 2441, 2455, 2457, 2460, 2464.
Д.З. Демидович, №№ 2470, 2473, 2474, 2475, 2477, 2481, 2482.
Д.З. Демидович. №№ 2527, 2528, 2532, 2535, 2538, 2546.
Д.З. Демидович, №№ 2590, 2594, 2595, 2597, 2600, 2614, 2625.
Д.З. Демидович, №№ 2644, 2645, 2648, 2653, 2654.
Кратные интегралы
Д.З. Демидович, №№ 2115, 2123, 2135а, 2137, 2146, 2150, 2152а.
Д.З. Демидович, №№ 2165
![]() 2167, 2181, 2193.
2167, 2181, 2193.
Д.З. Демидович, №№ 2240, 2243, 2244, 2247, 2248, 2265.
Д.З. Демидович, №№ 2241, 2242, 2243, 2249, 2253, 2555, 2557.
Д.З. Демидович, №№ 2213, 2227, 2231, 2262, 2269.
Свести двойной интеграл к повторному двумя способами, если G - область, ограниченная кривыми x = 1, y = x2, y = 2x (x ≤ 1).
Решение.
I способ. Область G изображена на Рис. 1, а. При каждом значении x из отрезка [0, 1] переменная yизменяется от x2 до 2x, т. е. область G можно представить в виде G = {(x, y): 0 ≤ x ≤ 1, x2 ≤ y ≤ 2x}. По формуле получаем
II способ. Чтобы воспользоваться формулой (*), нужно разбить область G на две части G1 и G2, как показано на Рис. 1, б. В области G1 переменная y изменяется от 0 до 1, а при каждом значении y переменная x изменяется от y/2 (значение x на прямой y = 2x) до (значение xна параболе y = x2). Поэтому по формуле (*) получаем
В области G2 переменная y изменяется от 1 до 2, а при каждом значении y переменная x изменяется отy/2 до 1. По формуле (*) получаем
Итак,
