
- •1. Формула Тейлора 2-го порядка с остаточным членом в форме Пеано для функции нескольких переменных.
- •2. Теорема о смешанных производных.
- •7.3.1. Теорема о смешанных производных
- •3. Формула Тейлора с остаточным членом в форме Лагранжа для функции одной переменной.
- •4. Формула Тейлора с остаточным членом в форме Лагранжа для функции нескольких переменных.
- •5. Критерий выпуклости функции. Доказательство . Следствие.
- •6. Критерий выпуклости функции. Доказательство . Следствие.
- •7. Лемма о знакопостоянной функции .
- •8. Необходимое условие глобального экстремума функции.
- •8.3.2. Необходимое условие глобального экстремума
- •9. Метод Лагранжа отыскания экстремумов (доказательство теоремы).
- •10. Лемма о системе линейных уравнений. Следствие.
- •1. Лемма о многочлене Тейлора .
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •3. Вывод формулы для . Частный случай для.
- •4. Асимптоты функции.
- •5. Разложение синуса по формуле Маклорена.
- •6. Разложение косинуса по формуле Маклорена.
- •7. Условие строгой монотонности функции (1-е утверждение теоремы 8.1).Теорема
- •8. Условие нестрогой монотонности функции (2-е утверждение теоремы 8.1).
- •9. Необходимое условие экстремума функции нескольких переменных.
- •10. Достаточное условие экстремума функции нескольких переменных.
5. Разложение синуса по формуле Маклорена.
Формула
Маклорена с остаточным членом в форме
Лагранжа для функции
 .
.
Производная
 -го
порядка функции
-го
порядка функции имеет вид
имеет вид
 .
.
Так
как
 ,
, ,
а,
,
а, то
то
 ,
,

 ,
,
 .
.
6. Разложение косинуса по формуле Маклорена.
3.
Формула Маклорена с остаточным членом
в форме Лагранжа для функции
 :
:
 .
.
Так
как
 ,
, ,
, ,
, то
то
 ,
,
7. Условие строгой монотонности функции (1-е утверждение теоремы 8.1).Теорема
8.1.
Если функция
 имеет производную на интервале
имеет производную на интервале ,
то справедливы
следующие утверждения.
,
то справедливы
следующие утверждения.
1.
Если

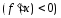 на интервале
на интервале то функция
то функция
 возрастает(убывает)
на этом интервале.
возрастает(убывает)
на этом интервале.
Доказательство
1.
Рассмотрим
две произвольных точки
 и
и из интервала
из интервала и пусть
и пусть .
Так как на отрезке
.
Так как на отрезке выполняются условия теоремы Лагранжа,
то найдется такая точка
выполняются условия теоремы Лагранжа,
то найдется такая точка ,
что справедливо равенство
,
что справедливо равенство
 .
(1)
.
(1)
Из условия теоремы и равенства (1) следует цепочка импликаций:

 на интервале
на интервале








 возрастает (убывает)
на интервале
возрастает (убывает)
на интервале
 .
.
8. Условие нестрогой монотонности функции (2-е утверждение теоремы 8.1).
Теорема
8.1. Если
функция
 имеет производную на интервале
имеет производную на интервале ,
то справедливы
следующие утверждения.
,
то справедливы
следующие утверждения.
2.
Производная

 на интервале
на интервале тогда и только
тогда, когда функция
тогда и только
тогда, когда функция
 не убывает(не
возрастает)
на этом интервале.
не убывает(не
возрастает)
на этом интервале.
Доказательство
2.
Необходимость.
Если

 на интервале
на интервале
 ,
то из формулы (1) следуют цепочки
импликаций:
,
то из формулы (1) следуют цепочки
импликаций:

 на интервале
на интервале








 не убывает (не
возрастает) на интервале
не убывает (не
возрастает) на интервале
 .
.
Достаточность.
Пусть
теперь
 не убывает (не возрастает) на интервале
не убывает (не возрастает) на интервале .
Отсюда, если
.
Отсюда, если
 —
произвольная точка интервала
—
произвольная точка интервала и
и ,
то
,
то

 .
.
Так
как функция
 дифференцируема в точке
дифференцируема в точке ,
то
,
то

 .
.
9. Необходимое условие экстремума функции нескольких переменных.
Теорема
8.7
(необходимое
условие экстремума). Функция
 имеет в точке
имеет в точке локальный экстремум. Тогда градиент
функции
локальный экстремум. Тогда градиент
функции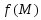 в точке
в точке равен нулевому вектору.
равен нулевому вектору.
Доказательство. Так как
 ,
,
то
для доказательства теоремы достаточно
доказать, что все частные производные
функции
 в точке
в точке равны нулю. Полагаем значения всех
переменных у функции
равны нулю. Полагаем значения всех
переменных у функции равными соответствующим координатам
точки
равными соответствующим координатам
точки ,
кроме переменной
,
кроме переменной .
Тогда получим функцию
.
Тогда получим функцию ,
которая зависит от одной переменной и
имеет в точке
,
которая зависит от одной переменной и
имеет в точке локальный экстремум. Из теоремы 8.2
следует, что
локальный экстремум. Из теоремы 8.2
следует, что
 ,
,
 .
.
10. Достаточное условие экстремума функции нескольких переменных.
Теорема
8.8
(достаточное условие экстремума). Функция
 в окрестности критической точки
в окрестности критической точки имеет непрерывные частные производные
2-го порядка. Справедливы следующие
утверждения:
имеет непрерывные частные производные
2-го порядка. Справедливы следующие
утверждения:
1.
Если функция
 положительно
определена, то
положительно
определена, то
 — точка локального минимума функции
— точка локального минимума функции
 .
.
2.
Если функция
 отрицательно
определена,
то
отрицательно
определена,
то
 — точка локального максимума функции
— точка локального максимума функции
 .
.
Доказательство.
Градиент
функции
 в точке
в точке равен нулю, так
равен нулю, так
как
 является критической точкой этой
функции. В этом случае формула (1) будет
иметь вид
является критической точкой этой
функции. В этом случае формула (1) будет
иметь вид

 .
.
Из
леммы 1 и 2 следует, что найдется такая
окрестность
 ,
в которой знак приращения
,
в которой знак приращения функции совпадает со знаком второго
дифференциала в точке
функции совпадает со знаком второго
дифференциала в точке
 этой функции.
этой функции.
1.
Если функция
 положительно определена, то
положительно определена, то в окрестности
в окрестности точки
точки
 ,
т.е.
,
т.е.
 в этой окрестности, значит,
в этой окрестности, значит, — точка локального минимума функции
— точка локального минимума функции .
.
2.
Если функция
 отрицательно определена, то
отрицательно определена, то в окрестности
в окрестности точки
точки
 ,
т.е.
,
т.е.
 в этой окрестности, значит,
в этой окрестности, значит, — точка локального максимума функции
— точка локального максимума функции .
.
