2. Формула Тейлора с остаточным членом в форме Пеано.

Следствие. Пусть функция 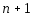раз дифференцируема в окрестноститочки. Тогда для любогосправедлива формула

. (4)

Доказательство. Достаточно установить, что 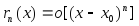. Имеем

.

Отсюда следует, что . Следовательно,

, где .■

Формула (4) называется формулой Тейлора порядка с остаточным членом в форме Пеано.

3. Вывод формулы для . Частный случай для.

Дифференциал функции

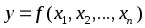
называется дифференциалом первого порядка или первым дифференциалом.

Пусть при фиксированных значениях приращений , первый дифференциалявляется дифференцируемой функцией переменных. Дифференциал первого порядка от функцииназываетсядифференциалом второго порядка или вторым дифференциалом функции и обозначается символом, т.е.

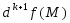Пусть уже определен дифференциал -го порядкафункции, и он является при фиксированных значениях приращений дифференцируемой функцией. Дифференциал первого порядка от функцииназываетсядифференциалом -го порядка функции и обозначается символом, т.е.

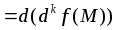
Заметим, что при построении каждое слагаемое в заменяется на слагаемых, поэтому количество слагаемых у дифференциалавраз больше количества слагаемых у дифференциала.

Найдем выражение для второго дифференциала :

. (9)

Частный случай. Для функции от двух переменных выражение для второго дифференциала имеет вид

.

Если смешанные производные второго порядка функции непрерывны, то они равны (теорема 7.1). В этом случае второй дифференциал функцииимеет вид

. ▲

4. Асимптоты функции.

Асимптоты графика функции — это прямые. Различают вертикальные и наклонные асимптоты. Среди наклонных асимптот выделяют горизонтальные асимптоты.

Прямая , параллельная оси, называется вертикальной асимптотой графика функции 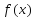, если один из пределов

,

или оба равны .

Если — вертикальная асимптота графика функции , то— точка разрыва функции2-го рода. Например, график функцииимеет вертикальную асимптоту, так как

, .

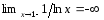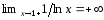Прямая называетсянаклонной асимптотой графика функции , еслиили.

Теорема 8.7. Прямая тогда и только тогда является наклонной асимптотой графика функции при 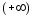,когда существуют

конечные пределы

, (6)

(, ).

Необходимость вытекает из следующих цепочек равенств:

—асимптота

.

.

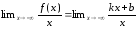
Достаточность. Пусть существуют конечные пределы (6). Тогда

.

Отсюда следует, что прямая является наклонной асимптотой графика функциипри. Аналогично рассматривается случай при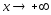.