9. Метод Лагранжа отыскания экстремумов (доказательство теоремы).

Теорема 8.10. Если 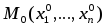— глобальный экстремум функции на множестве ,то найдется такой ненулевой набор чисел , что точка является решением системы уравнений

(4)

Доказательство. Из теоремы 8.10 следует, что система векторов

, ,…,,,, (5)

линейно зависима, где 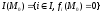. Следовательно, найдется такой ненулевой набор чисел, что равенство

(6)

является истиной.

Полагая при всех, разложение (6) перепишем в виде

(7)

Из равенства (7) следует, что -я координата вектора, находящегося в левой части равенства (7) равна нулю при любом. Так как-я координата линейной комбинации векторов равна сумме их-х координат, то из равенства (7) имеем

, . (8)

Левая часть равенства (8) равна частной производной функции Лагранжа по переменной в точке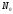, поэтому из равенства (7) следует

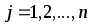, . (9)

Второе уравнение системы (4) в точке имеет вид

. (10)

Последнее равенство является истиной: , если, если же, то. Итак, равенство (10) справедливо при любом.

Из равенств (9) и (10) следует, что точка является решением системы уравнений (4) и числа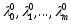образуют ненулевой набор

10. Лемма о системе линейных уравнений. Следствие.

Лемма. Система уравнений , ,имеет решения при любых значениях , если векторылинейно независимы.

Доказательство. Рассмотрим матрицу , строками которой являются векторы, матрицаимеет размер. В векторно-матричной форме данная система уравнений имеет вид:,гдеРанг матрицыравен(теорема о ранге матрицы). Следовательно, ранг системы ее столбцовравен, т.е.. Так как ранг части системы векторов не превосходит ранга всей системы, то

. (1)

Векторы системы имеют размерность , поэтому

. (2)

Из равенств (1) и (2) следует, что и, значит,

(3)

Из условия (3) вытекает, что вектор разлагается по системе. Это означает, что система уравненийимеет решение, поэтому система уравнений также имеет решения. ■

ВТОРЫЕ ВОПРОСЫ (0,5 БАЛЛА)

1. Лемма о многочлене Тейлора .

Пусть функция раз дифференцируема в точке. Многочлен

(1)

называется многочленом Тейлора порядка для функции в точке.

Лемма. Если является многочленом Тейлора для функции вточке , то справедливы следующие утверждения:

Доказательство. Найдем все производные многочлена Тейлора, который запишем в виде , где,:

………………………….

…………………………..

, .

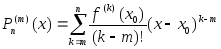
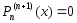Отсюда следует, что ■