6. Критерий выпуклости функции. Доказательство . Следствие.

Теорема 8.4. Функция дифференцируема на интервале. Следующие условия равносильны.

1. Функция выпукла вверх (вниз) на интервале .

2. Производная 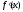не возрастает (не убывает) на интервале .

Доказательство

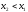21.Возьмем произвольную точку на интервалеи покажем, что график функции находится под (над) касательной, проведенной в точке, т.е.для любой точки. Возможны два случая: или .

Если , то, применяя теорему Лагранжа на отрезке, получим

, . (4)

Так как производная является невозрастающей (неубывающей) функцией, то изследует. Отсюда и равенства (4) имеем

.

Если же , то, применяя теорему Лагранжа на отрезке, получим

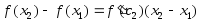, . (5)

Так как производная является невозрастающей (неубывающей) функцией, то из неравенстваследует. Отсюда и равенства (5) имеем

. ■

Следствие. Функция дважды дифференцируема на интервале. Тогда равносильны условия.

1. Функция выпукла вверх (вниз) на интервале .

2. Вторая производная неположительна (неотрицательна) на интервале .

Доказательство. Используя теорему 8.4 и второе утверждение теоремы 8.1, в котором роль функции играет производная, получим следующую цепочку равносильных утверждений:

функция выпукла вверх (вниз) на интервале

производная не возрастает (не убывает) на интервале

производная на интервале . ■

7. Лемма о знакопостоянной функции .

Лемма 1 . Если функция является знакопостоянной и

, то найдется такое число , что знак выражения

(3)

совпадает со знаком функци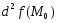и , если .

Доказательство. Перепишем формулу (2) в виде

.

Так как

,

то точка при любых значениях,…,,…,, одновременно не равных нулю, принадлежит сфере.

Квадратичная функция непрерывна при любых значениях

переменных, и значит, непрерывна на сфере, которая является замкнутым и ограниченным множеством (следствие из теоремы 4.9) . Так как функция является знакоопределенной, то>0 в каждой точке сферы.

Из 2-й теоремы Вейерштрасса следует, что функция 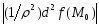принимает свое наименьшее значениев некоторой точке сферы, которое больше нуля, т.е.. Отсюда следует, что

. (4)

Так как , то из теоремы 3.11 вытекает, что если, то найдется такое число, что неравенствобудет справедливо, как только. Отсюда следует, что

.

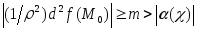Следовательно, знак выражения 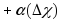совпадает со знаком, как только.■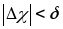

8. Необходимое условие глобального экстремума функции.

8.3.2. Необходимое условие глобального экстремума

Лемма. Система уравнений , ,имеет решения при любых значениях , если векторы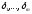линейно независимы.

Доказательство леммы приводится в приложении 3. ■

Следствие. Если система векторов линейно независима, то найдется такой вектор, что

(). (1)

Доказательство. Из леммы следует, что система уравнений

()

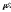
имеет решение , которое удовлетворяет условию (1).■

Теорема 8.10 (необходимое условие глобального экстремума функции). Функция определена на множестве

, .

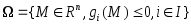Функции ипри любом дифференцируемы в точке глобального экстремума функции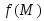,. Тогда система векторов

, ;,

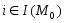где , линейно зависима.

Доказательство от противного, т.е. пусть система векторов

, ;

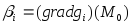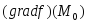
линейно независима. Из следствия к лемме следует, что найдется такой вектор 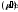, что

, , (,,).

Так как мерный векторудовлетворяет условию

,

то из свойства градиента следует, что можно построить такое число , что при всех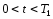

. (2)

Так как мерный векторудовлетворяет условию

, , (,),

то можно построить такое число (теорема 6.9), что при всехточка

(3)

Обозначим символом . Тогда при всехусловия (2) и (3) справедливы, что противоречит определению глобального экстремума.■