ПЕРВЫЕ ВОПРОСЫ (1 БАЛЛ)

1. Формула Тейлора 2-го порядка с остаточным членом в форме Пеано для функции нескольких переменных.

Теорема 7.3. Если функция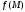в окрестноститочкиимеет непрерывные частные производные до второго порядка включительно, то

справедлива формула

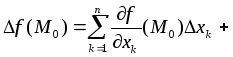
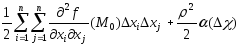. (5)

где ,,.

Доказательство. Если , то формулу (1) можно записать в виде:

.

Из формулы (9) в § 7.3 следует, что

.

Докажем, что

.

Так как производные второго порядка функции непрерывны, то

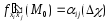, . (6)

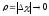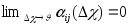Из условия следует, поэтому из условиявытекает. Теперь, учитывая равенство (6), имеем:

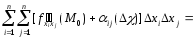
, где .

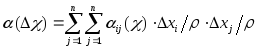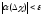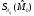Докажем, что . Для этого достаточно для каждогопостроить окрестность, в которой справедливо неравенство(теорема 3.12). Так как, то найдется окрестность, в которой. Обозначим символом. Тогда в окрестности, учитывая условия, справедливо неравенство

. ■

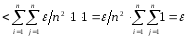Равенство (5) называется формулой Тейлора второго порядка с остаточным членом в форме Пеано.

2. Теорема о смешанных производных.

7.3.1. Теорема о смешанных производных

Лемма. Даны функция , определенная в окрестности точки

, и две функции одной переменной

, ,

где ,.Тогда справедливо равенство

.

Доказательство. Имеем следующие цепочки равенств:

, (1)

. (2)

Правые части формул (1) и (2) равны, значит, равны и левые их части, т.е.

. ■

Теорема 7.1. Функция имеет в некоторой окрестности точкисмешанные производныеи, которые в точкенепрерывны. Тогда в этой точке смешанные производные равны, т.е.

, .

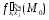
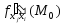Доказательство теоремы достаточно провести в случае функции двух переменных, т.е. и.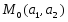

Рассмотрим две функции

, ,

где ,.

Функция имеет производную на отрезке. Тогда по формуле Лагранжа конечных приращений имеем:

(3)

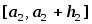Функция имеет производную на отрезке. Тогда по формуле Лагранжа конечных приращений имеем:

. (4)

Подставляя разность производных из формулы (4) в равенство (3), получим

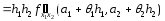. (5)

Совершенно аналогично получим выражение для приращения функциив точке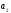, применяя дважды формулу Лагранжа конечных приращений:

. (6)

Из леммы следует, что левые части равенств (5) и (6) равны, значит, равны и их правые части, т.е.

. (7)

После сокращения обеих частей равенства (7) на произведение , получим равенство, в котором перейдем к пределу прии

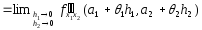. (8)

Так как частные производные инепрерывны в точке, то из равенства (8) вытекает требуемое равенство

.