Решение системы уравнений по формулам Крамера.

Исходная система уравнений имеет вид:

1. Из коэффициентов при неизвестных составляем главный определитель системы:

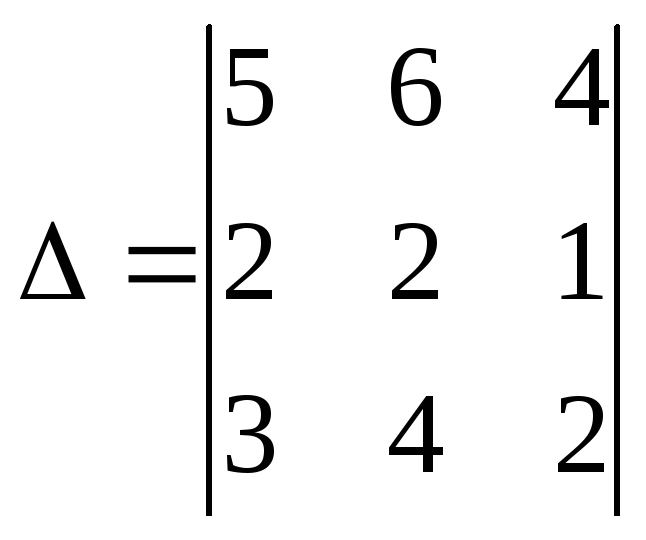
2. По правилу Сарруса находим значение этого определителя:

=5∙2∙2+3∙6∙1+2∙4∙4-3∙2∙4-2∙6∙2-5∙4∙1= 20+18+32-24-24-20=2≠0

3. Заменяя столбцы коэффициентов при каждом из неизвестных в главном определителе системы столбцом свободных членов, мы находим соответствующие вспомогательные определители системы:

4. В целях рациональности вычисления находим вспомогательные определители, применяя теорему Лапласа к первому, второму, третьему столбцу, соответственно:

4.1

4.2

4.3

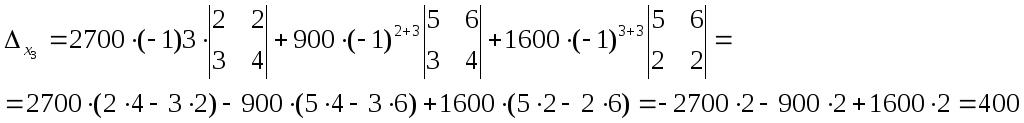
5. По формулам Крамера находим неизвестные:

Решение окончено.

Проверка:

Ответ:ежедневный выпуск продукции составляет200 шт.изделияS₁,150 шт.изделияS₂и200 шт.изделияS₃.

Задача № 2

Определить, имеет ли матрица Aобратную, и если имеет, то вычислить ее:

Решение

1)Вычисляем определитель матрицыА, применяя теорему Лапласа к первой строке:

2)Выписываем транспонированную матрицуА^Т:

3)Строим присоединенную матрицу. Ее элементы представляют собой алгебраические дополнения соответствующих элементов транспонированной матрицыА^Т.

Выписываем присоединенную матрицу:

4)Находим обратную матрицу по формуле:

Проверка.Воспользуемся определением обратной матрицы :

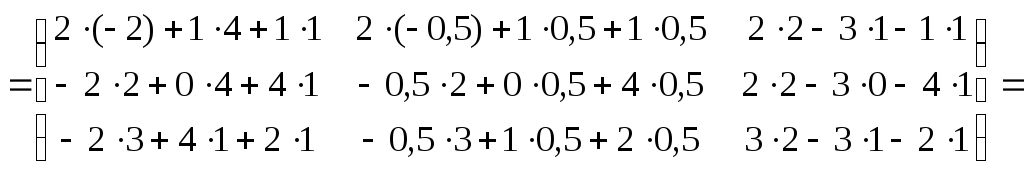
Задача № 3

В таблице приведены данные об исполнении баланса. Используя модель Леонтьевамногоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной в 1,2 раза.

Вариант №1.
№	Отрасль	Потребление		Конечный продукт	Валовой продукт
	Энергетическая	100	160	240	500
	Машиностроение	275	40	85	400

Решение

1)Вычисляем коэффициенты прямых затратa_ij, показывающие, какой объем продукцииi-ой отрасли идет на производство одной единицы продукцииj-ой отрасли:

2)Выписываем столбец валового выпускаX, столбец нового конечного выпускаY, а также матрицу прямых затратА.

3)Вычисляем матрицуE-A

4)Вычисляем матрицу полных затратS=(E-A)^-1.Каждый элементs_ijэтой матрицы показывает величину валового выпускаi-ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продуктаj-ой отрасли.

4.1.Вычисляем определитель

4.2.Находим транспонированную матрицу

4.3.Строим присоединенную матрицу:

4.4.Находим обратную матрицу:

5)Вычисляем новый вектор валового выпуска:

6)Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:

№	Отрасль	Потребление		Конечный продукт	Валовой продукт
	Энергетическая	186,4	265,6	480	932
	Машиностроение	512,6	66,4	85	664

Проверка: