КОМПЛЕКСНЫЕ ЧИСЛА

Комплексные числа

Комплексные числа. Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i2=-1. Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х. Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой частью z, у = Im z. Два комплексных числа z1=x1+iy1 и z2=х2+iy2 называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х1=х2, y1=у2. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными.

Их изображение на комплексной плоскости. Всякое комплексное число z=x+iy можно изобразить точкой М(х;у) плоскости ОXY такой, что х=Rez, у=Imz. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z=х+iy

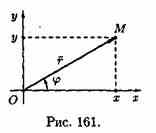
Модуль и аргумент комплексного числа. Комплексное число z=х+iy можно задавать с помощью радиус-вектора r=ОМ=(х;у). Длина вектора r, изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r.

Величина угла между положительным направлением действительной оси и вектором r, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Argz или φ.

Аргумент комплексного числа z=0 не определен. Аргумент комплексного числа z≠0 — величина многозначная и определяется с точностью до слагаемого 2πk

Алгебраическая, тригонометрическая, показательная формы записи комплексного числа. в виде z=х+iy называют алгебраической формой комплексного числа.

запись комплексного числа называется тригонометрической формой.z=rcosφ+irsinφ или z=r(cosφ+isinφ)___( при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z, т. е. считать φ=argz.)

комплексное число z=r(cosφ+isiπφ) можно записать в так называемой показательной (или экспоненциальной) форме z=rеiφ, где r=|z| — модуль комплексного числа, а угол φ=Argz=argz+2kp

Операции над комплексными числами. Суммой двух комплексных чисел z1=х1+iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством

z1+z2=(x1+x2)+i(y1+y2). Сложение комплексных чисел обладает переместителъным (коммутативным) и сочетательным (ассоциативным) свойствами:

z1+z2=z2+z1

(z1+z2)+z3=z1+(z2+z3).

Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.

Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:

z=z1-z2=(x1-x2)+i(y1-y2).

модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости

Произведением к омплексных чисел z1 =х1 +iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством

z=z1 z2 =(x1 x2- у1 у2)+i(x1 y2+y1x 2 )

z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2)= z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)).

Деление:

Для тригонометрической формы комплексного числа формула деления имеет вид

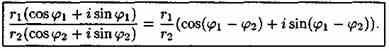
Корнем n-й степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, т. е., если ωn= z.

Решение уравнений с комплексными числами. Рассмотрим сначала простейшее квадратное уравнение

Z² = a,

где а - заданное число,

z - неизвестное.

На множестве действительных чисел это уравнение:

1) имеет один корень z = 0, если а = 0;

2) имеет два действительных корня z1,2 = , если а>0;

3) не имеет действительных корней, если а<0.

На множестве комплексных чисел это уравнение всегда имеет кореньВОТ ТУТ НЕ УВЕРЕНА!!НУЖНО ДОПИСАТЬ!!!

Формула Муавра zⁿ=(r(cosφ+isinφ))ⁿ=rⁿ(cosnφ+isinnφ).