1.10.2. Действия над непрерывными функциями
Теорема
1.11. Если
функции
и
непрерывны в точке
,
то в этой точке также непрерывны следующие
функции:
1)
;
2)
;
3)
,
где
.
Д о к о з а т е л ь с т в о. Используем второе определение непрерывности функции в точке и свойства пределов, получим:
1)
;
2)
;
3)
.
Так как пределы от рассмотренных функций равняются значениям этих функций в предельной точке, то эти функции непрерывны.
1.10.3. Непрерывность элементарных функций
1.
Многочлен
является непрерывной функцией, так как
он образован с помощью алгебраических
действий сложения и умножения непрерывных
функций: постоянных коэффициентов
и функцииy
= х (теорема
1.11).
2. Докажем, что функция y = sinx является непрерывной. Найдем
.
Здесь
использовали первый замечательный
предел и то, что произведение бесконечно
малой функции х
на ограниченную функцию
является бесконечно малой. Так как
,
то по первому определению непрерывности
функции функцияy
= sinx
является непрерывной.
3. Докажем непрерывность функции y = lnx.
Найдем
.
Здесь был использован второй замечательный предел.
Аналогично можно доказать непрерывность других элементарных функций.
1.10.4. Свойства непрерывных функций
Свойство 1. Функция y = f(x) непрерывная на отрезке [a, b] принимает свое наибольшее M и наименьшее m значения на этом отрезке.
Свойство 2. Функция непрерывная на отрезке хотя бы один раз принимает любое значение, заключенное между наименьшим и наибольшим значениями.
Свойство 3. Если непрерывная функция в граничных точках отрезка принимает значения противоположных знаков, то она на этом отрезке хотя бы один раз обращается в нуль.
Свойство
4. Если
функция y
= f(u)
непрерывна
в точке
,
а функцияu
= φ
(u)
непрерывна в точке
,
то сложная функция
является непрерывной в точке
.
1.10.5. Точки разрыва функций
Точка
называется точкой разрыва функцииy
= f(x),
если в этой точке функция не является
непрерывной.
Определение
1. Точка
называется устранимой точкой разрыва
функцииy
= f(x),
если существуют односторонние пределы
функции в этой точке, равные между собой,
но не равные значению функции в этой
точке
.
|
Рис. 10 |
Например,
функция
|
имеет точку разрыва прих
= 2 (рис. 10). 
.
Определение
2. Точка
называется точкой разрыва функцииy
= f(x)
первого рода, если существуют односторонние
пределы функции в этой точке, не равные
между собой, т. е.
(рис. 11, рис. 12).
|
Рис. 11 |
Рис. 12 |
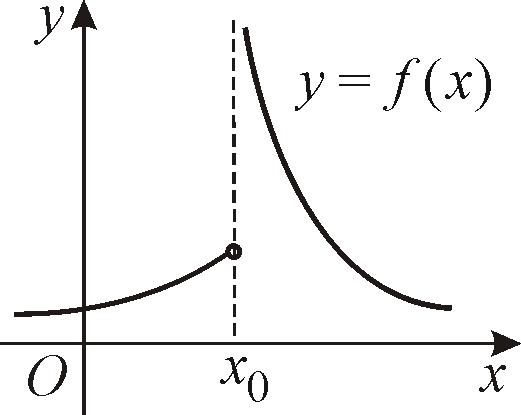
Определение
3. Точка
называется точкой разрыва функцииy
= f(x)
второго рода, если она не является
точкой разрыва первого рода (рис. 13,
рис. 14).
|
Рис. 13 |
Рис. 14 |
Пример
1.18. Найти
точку разрыва функции
и построить график функции.
Функция не определена при x = 1. Найдем односторонние пределы функции в этой точке.
,
.
|
Рис. 15 |
Функция имеет точку разрыва второго рода x = 1 (рис. 15). Найдем пределы функции при x.
Следовательно, y = 1 является горизонтальной асимптотой функции.
|
.