Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009

степень внутренней статической неопределимости;

формулу для подсчета внешних лишних связей;

формулу для подсчета внутренних лишних связей;

внешне статически неопределимая стержневая конструкция;

внутренне статически неопределимая стержневая конструкция;

статически неопределимая стержневая конструкция общего вида;

свойства статически неопределимых стержневых конструкций;

основная задача расчета стержневых статически неопределимых конструкций;

частная задача расчета стержневых статически неопределимых конструкций;

методырасчетастатическинеопределимыхстержневых конструкций;

суть метода сил.

Проверьте, как Вы умеете определять для статически неопределимых стержневых конструкций:

степень полной статической неопределимости;

степень внешней статической неопределимости;

степень внутренней статической неопределимости.

21

М-8. МЕТОД СИЛ

8.0. Введение в модуль

Основными целями модуля являются:

получение формул для определения внутренних усилий в произвольной плоскойстатически неопределимой стержневой конструкции;

рассмотрение особенностей определения внутренних усилий с учетом симметрии плоской статически неопределимой стержневой конструкции;

получение матричных формул для определения внутренних усилий в плоской статически неопределимой стержневой конструкции;

рассмотрение особенностей определения перемещений в плоской статически неопределимой стержневой конструкции.

Структураизучаемогомодуля включаетследующие учебныеэлементы: 1. Расчет методом сил произвольной плоской статически неопреде-

лимой стержневой конструкции. 2. Поверки метода сил.

3. Особенности расчета методом сил симметричных плоских статически неопределимых стержневых конструкций.

4. Матричная форма расчета методом сил плоских статически неопределимых стержневых конструкций.

5. Определение перемещений в плоских статически неопределимых стержневых конструкциях.

При изучении учебных элементов рекомендуется использование сле-

дующей литературы: [1, c. 309 – 391]; [3, c.193 – 249]; [4, c. 251 – 257, 293 – 304, 341 – 354]; [5, c. 238 – 287 – 48].

8.1.Расчет методом сил произвольной плоской статически неопределимой стержневой конструкции

8.1.1. Постановка задачи

Задана произвольная плоская статически неопределимая стержневая конструкция (рис. 8.1), для которой считаются известными все размеры геометрической схемы и поперечных сечений стержней

22

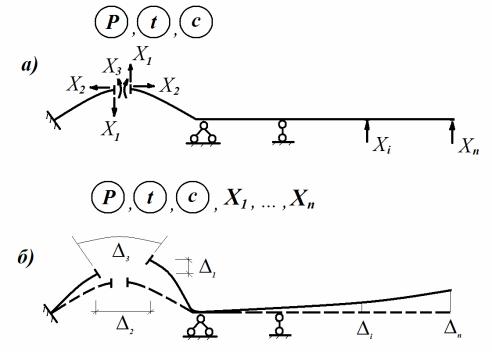
так, чтобы преобразованная система была геометрически неизменяемой с необходимым числом связей и, следовательно, статически определимой. Поскольку возможны различные схемы удаления лишних связей в заданной системе, то возможно получение нескольких вариантов статически определимых систем.

Статическая эквивалентность полученной статически определимой системы заданной системе достигается приложением к ней в качестве дополнительных внешних воздействий реакций удаленных лишних связей

X1 ,...,Xn (рис. 8.3, а).

Рис. 8.3

При дальнейшем расчете эти реакции подлежат первоочередному определению и поэтому они называются основными неизвестными метода сил. И, поскольку, основные неизвестные являются реакциями, то они имеют статическую природу.

Для достижения кинематической эквивалентности двух систем вводятся условия обращения в ноль полных перемещений (рис. 5.3, б)

возникающих в статически определимой системе по направлению основных неизвестных. Так как эти перемещения порождаются основными неизвестными и заданными внешними воздействиями, то они являются функциям этих величин и условия (8.3) можно записать в следующем виде

24

1 X1,..., Xn , P,t,c 0,

..................................... (8.4)n X1,..., Xn , P,t,c 0.

Поскольку заданная стержневая конструкция считается линейно деформируемой системой, то дополнительные условия (8.4), согласно принципу суперпозиции, принимают вид

1X1 ... 1Xn 1P 1t 1c 0,

....................................................... (8.5)

nX1 ... nXn nP nt nc 0.

Входящие в (8.5) величины имеют следующий смысл: iX j i, j 1,...,n –

частичное перемещение (простое или обобщенное) в основной системе по направлению основного неизвестного № i , вызванное действием основного неизвестного X j ; iP , it , ic i 1,...,n – частичное перемещение (про-

стое или обобщенное) в основной системе по направлению основного неизвестного № i , вызванное действием, соответственно, нагрузки, температуры или осадки опор.

Так как изменения частичного перемещения iX j и основного неизвестного X j связаны прямой пропорциональной зависимостью, то

где ij – единичное перемещение (простое или обобщенное) в основной системе по направлению основного неизвестного № i от действия безраз-

Полученные уравнения (8.7) представляют собой систему неоднородных линейных алгебраических уравнений относительно основных неизвестных

X1 ,...,Xn и называются каноническими уравнениями метода сил. Они

имеют кинематическую природу, так как каждое такое уравнение выражает равенство нулю полного перемещения в основной системе по направле-

25

нию соответствующего основного неизвестного от действия всех основных неизвестных, а также нагрузки, температуры и осадки опор.

Входящие в эти уравнения единичные перемещения ij в качестве

множителей при основных неизвестных называются коэффициентами канонических уравнений метода сил. В зависимости от соотношений между индексами различают два вида таких коэффициентов. В случае если i j , то соответствующие коэффициенты называются главными коэф-

фициентами, и они удовлетворяют условию строгой положительности

ii 0 i 1,...,n .

В случае если i j , то соответствующие коэффициенты называются побочными коэффициентами, и они удовлетворяют условию взаимности

или осадки опор называются свободными членами канонических уравнений.

Наряду с развернутой формой записи канонических уравнений в виде (8.7) существует матричная форма записи таких уравнений

Здесь A – матрица коэффициентов канонических уравнений

P , t , c – векторы свободных членов канонических уравнений, соответственно, от действия нагрузки, температуры или осадки опор

X – искомый вектор основных неизвестных

X1

X .Xn

26

8.2.3. Определение коэффициентов и свободных членов

Для определения коэффициентов канонических уравнений метода сил нужно последовательно загрузить основную систему безразмерными

лия mj ,qj ,nj и построить их эпюры. Такие внутренние усилия и их эпюры

называются единичными, а соответствующие им схемы нагружения счи-

таются единичными состояниями основной системы.

После нахождения единичных внутренних усилий mj ,qj ,nj и построения их эпюр производится вычисление коэффициентов ij по формуле Максвелла – Мора. При этом роль нагрузки играют безразмерные силы

Необходимость учета отдельных слагаемых, как уже отмечалось ранее, зависит от вида стержневой конструкции.

Для определения свободных членов канонических уравненийiP i 1,...,n необходимо рассмотреть основную систему под действием

нагрузки, найти внутренние усилия MP0 ,QP0 , NP0 и построить их эпюры. Такие внутренние усилия и их эпюры называются грузовыми, а соответствующая им схема нагружения считается грузовым состоянием основной системы.

После нахождения грузовых внутренних усилий MP0 ,QP0 , NP0 и построения их эпюр производится вычисление свободных членов iP по формуле Максвелла – Мора, которая с учетом введенных обозначений принимает вид

it i 1,...,n необходимо рассмотреть основную систему под действием температуры, найти для каждого стержня удельный температурный пере-

27

пад t , приращение температуры на оси tо и построить эпюры этих величин. После нахождения величин t и tо производится вычисление свободных членов it по формуле температурных перемещений для плоских статически определимых стержневых конструкций

it ni tо mi t ds .

k l

Для вычисления свободных членов канонических уравненийic i 1,...,n используется формула для определения перемещений в плоских статически определимых стержневых конструкциях от заданных смещений опор c j

ic rjicj . j

Входящие в эту формулу единичные опорные реакции rji считаются найденными при рассмотрении единичных состояний основной системы.

8.2.4. Решение канонических уравнений

Математической формой канонических уравнений метода сил является система неоднородных линейных алгебраических уравнений

Связь между величинами, входящими в системы уравнений (8.9) и (8.7), определяется соотношениями

aij ij , x j X j , bi iP it ic .

Поэтому для решения канонических уравнений метода сил применяют численные методы решения систем линейных алгебраических уравнений. При числе основных неизвестных не превышающем 103 обычно применяется метод Гаусса. При большем числе основных неизвестных применяют итерационные методы, например, метод простой итерации.

8.2.5. Определение внутренних усилий заданной системы

Для определения внутренних усилий, которые возникают в заданной системе от приложенных к ней внешних воздействий, используется основная система метода сил и результаты ее расчета следующим образом.

28

При нахождении коэффициентов канонических уравнений ij основ-

и основная система считается линейно деформируемой, то внутренние усилия, возникающие в ней от действия X1 ,...,Xn , будут равны

ствием, соответственно, температуры и осадки опор. При этом в соответствии со свойствами статически определимых систем в основной системе не возникают внутренние усилия от этих внешних воздействий. Следовательно

Таким образом, для определения внутренних усилий в заданной системе необходимо, в соответствии с принципом суперпозиции, сложить внутренние усилия, полученные в основной системе от основных неизвестных X1 ,...,Xn , заданной нагрузки, температуры и осадки опор. Следо-

вательно, при совместном действии на заданную систему нагрузки, температуры и осадки опор формулы для определения внутренних усилий, с учетом (8.9) и (8.10), имеют вид

M m1X1 ... mn Xn M P0 ,

29

В случае раздельного действия нагрузки, температуры и осадки опор формулы (8.11) принимают вид:

для нагрузки

Mm1X1 ... mn Xn M P0 , Q q1X1 ... qn Xn QP0 ,

Nn1X1 ... nn Xn NP0 .

для температуры или осадки опор

Mm1X1 ... mn Xn , Q q1X1 ... qn Xn ,

Nn1X1 ... nn Xn.

8.2.Поверки метода сил

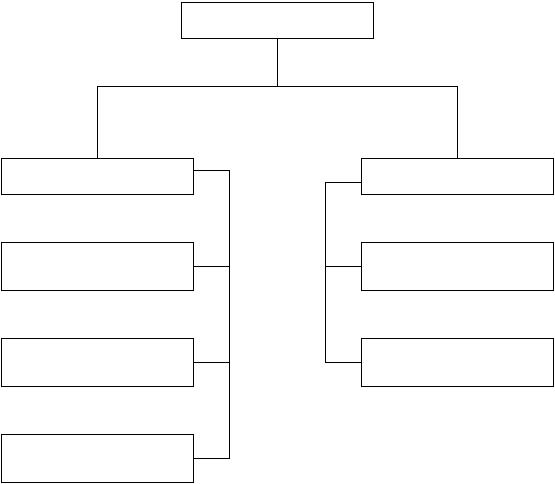
Поверки метода сил имеют следующую структуру:

Поверки МС

3.Алгебраические

и преследуют следующие цели:

30