
- •Оглавление
- •Методика обработки полной информации
- •Составление сводной таблицы информации в порядке возрастания показателя надежности
- •2. Составление статистического ряда
- •3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения
- •4. Проверка информации на выпадающие точки
- •5. Выполнение графического изображения опытного распределения показателя надежности
- •6. Определение коэффициента вариации
- •7. Выбор теоретического закона распределения для выравнивания опытной информации
- •7.1. Использование для выравнивания распределения опытной информации знр
- •7.2. Использование для выравнивания распределения опытной информации зрв
- •8. Оценка совпадений опытного и теоретического законов распределения показателя надежности по критерию согласия Пирсона
- •9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности
- •9.1.Определение доверительных границ рассеивания при законе нормального распределения
- •9.2.Определение доверительных границ при законе распределения Вейбулла
- •10. Определение абсолютной и относительной предельных ошибок переноса опытных характеристик показателя надёжности
- •Список литературы

|
|

Оглавление
Методика обработки полной информации 3
1.Составление сводной таблицы информации в порядке возрастания показателя надежности 3
2. Составление статистического ряда 4
3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения 5
4. Проверка информации на выпадающие точки 6
5. Выполнение графического изображения опытного распределения показателя надежности 7
6. Определение коэффициента вариации 9
7. Выбор теоретического закона распределения для выравнивания опытной информации 10
8. Оценка совпадений опытного и теоретического законов распределения показателя надежности по критерию согласия Пирсона 18
9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности 21
10. Определение абсолютной и относительной предельных ошибок переноса опытных характеристик показателя надёжности 25
Список литературы 27
Методика обработки полной информации
Составление сводной таблицы информации в порядке возрастания показателя надежности
Таблица 1 – Информации о доремонтных ресурсах двигателя
|
1 |
1124 |
|
2 |
1212 |
|
3 |
1320 |
|
4 |
1350 |
|
5 |
1480 |
|
6 |
1540 |
|
7 |
1620 |
|
8 |
1620 |
|
9 |
1670 |
|
10 |
1670 |
|
11 |
1900 |
|
12 |
1950 |
|
13 |
1970 |
|
14 |
1980 |
|
15 |
2010 |
|
16 |
2070 |
|
17 |
2190 |
|
18 |
2220 |
|
19 |
2290 |
|
20 |
2300 |
|
21 |
2370 |
|
22 |
2440 |
|
23 |
2600 |
|
24 |
2820 |
|
25 |
2960 |
|
26 |
3150 |
|
27 |
3400 |
|
28 |
3720 |
2. Составление статистического ряда
Для упрощения дальнейших расчетов составляется статистический ряд
Когда N>25 составляется статистический ряд. В данном примере N=28 целесообразно составить статистический ряд
Информация
разбивается на интервалы. Число интервалов
n=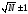 ,
,
где
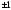 означает округление до ближайшего
большого целого числа.
означает округление до ближайшего
большого целого числа.
В
нашем примере n= =6.
Принимаем число интерваловn=6
=6.
Принимаем число интерваловn=6
Длина интервалов
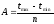 ,
(2.1)
,
(2.1)
где
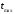 ,
,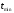 - наибольшее и наименьшее значение
показателя надежности в сводной таблице
1.
- наибольшее и наименьшее значение
показателя надежности в сводной таблице
1.
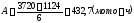
Таблица 2 – Статистический ряд
|
Интервал, тыс. мото-ч |
1124-1556,7 |
1556,7-1989,3 |
1989,3-2422 |
2422-2854,7 |
2854,7-3287,3 |
3287,3-3720 |
|
Опытная частота, mi |
6 |
8 |
7 |
3 |
2 |
2 |
|
Опытная вероятность, Pi |
0,21 |
0,29 |
0,25 |
0,11 |
0,07 |
0,07 |
|
Накопленная опытная вероятнсть |
0,21 |
0,50 |
0,75 |
0,86 |
0,93 |
1,00 |
Определение опытной вероятности
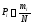 ,
(2.2)
,
(2.2)
где
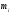 - опытная частота в i-том
интервале статистического ряда;
- опытная частота в i-том
интервале статистического ряда;
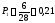
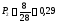


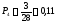
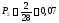
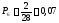

Определение накопленной опытной вероятности
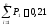
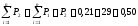
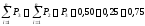
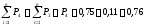
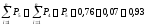
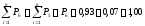
3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения
При наличии статистического ряда когда N>25 находим по формуле
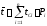 , (3.1)
, (3.1)
где tci – значение середины i-го интервала
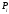 -
опытная вероятность i-го
интервала
-
опытная вероятность i-го
интервала
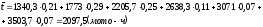
Определение квадратического отклонения – характеризуется рассеиванием среднего значения показателя надежности
При N>25 определяется по формуле
 (3.2)
(3.2)

4. Проверка информации на выпадающие точки
Грубую
проверку выполняют по правилу
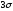 :
:
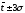 ,
(4.1)
,
(4.1)
Нижняя граница будет равна
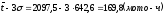
Верхняя граница будет равна
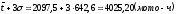
Наименьший
доремонтный ресурс двигателя
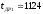 мотто-ч. Следовательно, эта точка
информации действительна и должна быть
учтена в дальнейших расчетах. Наибольший
ресурс двигателя
мотто-ч. Следовательно, эта точка
информации действительна и должна быть
учтена в дальнейших расчетах. Наибольший
ресурс двигателя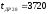 мото-ч.
Эта точка информации действительна и
должна быть учтена в дальнейших расчетах.
мото-ч.
Эта точка информации действительна и
должна быть учтена в дальнейших расчетах.
Проверка по критерию Ирвина
Фактическое значение критерия
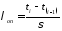 ,
(4.2)
,
(4.2)
где ti и t(i-1)смежные точки информации
При λоп≤ λт-точка является действительной
При λоп≥ λт-точка является выпадающей
В данном примере
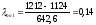
Верхняя граница :

По таблице №4 методички находим, что при β=0,95 и N=28, λт=1,2

Первая точка информации является действительной т.к λоп1=0,14≤ λт=1,2
Последняя точка информаций также является действительной т.к λоп28=0,50≤ λт=1,2
