Методика эксперимента.

Для экспериментального измерения магнитных полей широко используется эффект Холла. Этот эффект, открытый Холлом в 1879 году, представляет собой явление возникновения разности потенциалов в направлении, перпендикулярном магнитному полю и току.

Существование эффекта Холла может быть непосредственно продемонстрировано следующим образом (рис. 2.1).

Если металлическую пластинку, вдоль которой течёт ток , поместить в перпендикулярное к ней магнитное поле, то между точками А и В, расположенными на противоположных сторонах пластинки, возникает разность потенциалов.

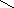
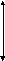
Возникающая разность потенциаловпропорциональна произведению силы тока на индукцию магнитного поляи обратно пропорциональна толщине пластинки:

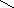
, (2.4)

где d- толщина пластинки; К- постоянная Холла.

Если ток обусловлен переносом электронов с зарядом е, то в магнитном поле на них действует сила Лоренца, отклоняющая их в направлении, перпендикулярном к направлению тока. В результате этого заряды начнут скапливаться у края пластинки В до тех пор, пока вызванное ими электрическое поле не уравновесит действие магнитной силы.

По формуле Лоренца сила, действующая на заряд, в нашем случае, когда направление тока перпендикулярно магнитному полю, равна:

, (2.5) где v средняя скорость движения заряда в направлении тока.

Напряжённость электрического поля, обусловленного появлением разности потенциалов , будет:

, ( 2.6) где bширина пластины.

Следовательно, электрическая сила, действующая на заряд, равна

. (2.7)

Стационарное состояние наступит при равенстве сил , откуда получаем соотношение:

. (2.8)

Среднюю скорость движения зарядов в проводнике получим, используя соотношение между силой тока, числом зарядов в единице объёма проводникаnи скоростью их движения:,

откуда

. (2.9)

Подставляя соотношение (2.9) в (2.2), получим:

. (2.10)

Таким образом, в соответствии с экспериментальной формулой (2.5) величина разности потенциалов пропорциональна произведениюи обратно пропорциональна толщине пластиныd. Постоянная К оказывается равной:

. (2.11)

Так как заряд электронов отрицателен, постоянная К в металлах должна быть отрицательной, и её численное значение должно определяться зарядом электрона и числом свободных электронов в единице объёма металла n.

Вывод выражения для постоянной К (2.11) неточен. На самом деле, нельзя выражать силу Лоренца, действующую на заряд в магнитном поле, через среднюю скорость заряда. Если учесть, что на длине свободного пробега электрона его скорость в направлении распространения тока равномерно возрастает, то в выражение для К войдёт ещё числовой множитель 2/3; тогда

. (2.11а)

В электролитах с их ионной проводимостью заметный эффект отсутствует. Это объясняется тем, что ионы намного тяжелее электронов, поэтому имеют значительно меньшие скорости по сравнению с электронами.

Эффект Холла находит широкое применение для исследования физических свойств полупроводников, металлов и для измерения индукции магнитных полей. Экспериментально можно определить I, B, d, и V₁-V₂ =и из формулы (2.5) найти величину постоянной Холла:

. (2.12)