Сисемный анализ 2 группа 4 бригада экстремум
.docx
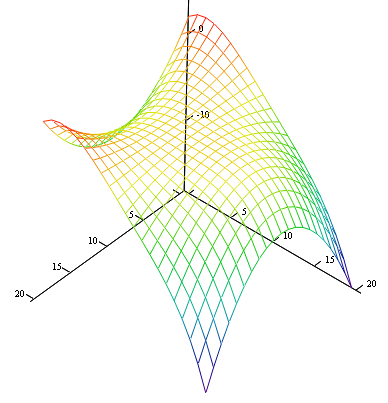
Рассчитать экстремум функции двух переменных и построить график.

Решение:
1. Найдем частные производные.
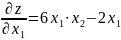
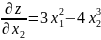
2. Решим систему уравнений.
 =
0
=
0
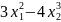 =
0
=
0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
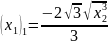

или
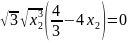
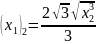
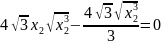
или
Откуда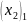 =
0;
=
0;
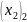 = 1/3;
= 1/3;
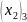 =
0;
=
0;
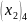 = 1/3
= 1/3
Данные
значения y
подставляем в выражение для x.
Получаем:
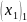 =
0;
=
0;
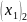 = -2/9;
= -2/9;
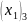 = 0;
= 0;
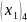 =
2/9
=
2/9
б)
Из первого уравнения выражаем
 и подставляем во второе уравнение:
и подставляем во второе уравнение:

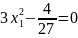
Откуда = -2/9; = 2/9
Данные
значения
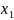 подставляем в выражение для
Получаем:
=
1/3;
=
1/3
подставляем в выражение для
Получаем:
=
1/3;
=
1/3
Количество критических точек равно 3.
M1(0;0), M2(-2/9;1/3), M3(2/9;1/3)
3. Найдем частные производные второго порядка.

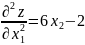
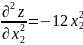
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(0;0)
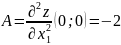

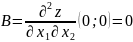
AC - B2 = 0, то вопрос о наличии экстремума остается открытым.
Вычисляем значения для точки M2(-2/9;1/3)
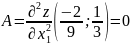
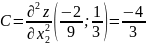

AC - B2 = -16/9 < 0, то глобального экстремума нет.
Вычисляем значения для точки M3(2/9;1/3)


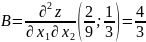
AC - B2 = -16/9 < 0, то глобального экстремума нет.
Вывод: Глобального экстремума нет.