
kurs_final2
.pdfСанкт-Петербургский Государственный университет телекоммуникаций имени профессора М.А.Бонч-Бруевича
Кафедра ТЭЦ
Курсовая работа по ОТЦ на тему: «Расчёт LC- и ARC-фильтров».
25 вариант.
Выполнил: студент группы МТО-85 Осипов Н.С. Проверила: доцент кафедры ТЭЦ Глебова М.С.
Санкт-Петербург 2010
1
Содержание
1. Расчёт LC-фильтра …....................................................................................................... |
3 |
|
1.1 |
Содержание задания …............................................................................................ |
3 |
1.2 |
Проектирование схемы фильтра …........................................................................ |
3 |
1.3 |
Определение передаточной функции фильтра …............................................... |
5 |
1.4 |
Расчёт характеристики ослабления проектируемого фильтра …..................... |
5 |
1.5 |
Моделирование фильтра на ПК ….......................................................................... |
6 |
2. Расчёт ARC-фильтра ….................................................................................................... |
7 |
|
2.1 |
Содержание задания …........................................................................................... |
7 |
2.2 |
Построение схемы …............................................................................................... |
8 |
2.3 |
Расчёт параметров элементов ARC-фильтра …................................................... |
8 |
2.4 |
Расчёт частотных зависимостей параметрических чувствительностей АЧХ и |
12 |
ФЧХ звена АВТ-структуры …............................................................................................... |
|
|
2.5 |
Расчёт характеристики ослабления фильтра на ПК …........................................ |
15 |
2
1. Расчёт LC-фильтра
1.1 Содержание задания
Рассчитать LC-фильтр, полагая, что его элементы имеют пренебрежимо малые потери. Исходные данные для варианта 25 (код 122):
Тип фильтра |
ФНЧ |
|
|
|
|
Вид аппроксимации |
Аппроксимация по Чебышеву |
|
|
|
|
Режим работы фильтра |
Односторонняя нагрузка при заданном |
|
|
входном напряжении |
|
|
|
|
C |
0.5 |
дБ |
|
|
|
M |
1.5 |
дБ |
|
|
|
Допустимая неравномерность |
1.25 дБ |
|
характеристики ослабления фильтра в |
|
|
полосе пропускания ∆a |
|
|
|
|
|
Граничная частота полосы пропускания f0 |
5.5 |
кГц |
|
|
|
Граничная частота полосы задерживания fk |
10.8 кГц |
|
|
|
|
Гарантированное ослабление в полосах |
52 дБ |
|
задерживания a0 |
|
|
|
|
|
Величина нагрузочного сопротивления R2 |
600 Ом |
|
|
|
|
+
 +
+
U0 |
R2 |
U2 |
1.2 Проектирование схемы фильтра
Для расчёта фильтра используется методика, согласно которой схема, параметры элементов и характеристики проектируемого фильтра находятся с помощью частотного преобразования фильтра-прототипа нижних частот (ФПНЧ).
Прежде всего следует определить порядок ФПНЧ, который, для фильтров с характеристиками Чебышева определяется по формуле:
3
n≥ |
a0 6−10lg 100.1Δa−1 |
|||||
|
|
|
|
|
||
20lg |
|
2 |
−1 |
|||
|
||||||
|
wk wk |
|||||
В этом выражении нормированная граничная частота полосы задерживания ФПНЧ рассчитывается по формуле:
wk =f k
f 0
wk =1.964 n=5.577
При округлении рассчитанного значения n до ближайшего большего целого числа получим: n=6 .
Схема ФПНЧ 6-ого порядка для режима заданного входного напряжения:
|
a |
6 |
a4 |
a2 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
U0 |
|
a5 |
a3 |
a1 |
1 |
U2 |
Значения параметров элементов ФПНЧ:
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
|
|
|
|
|
|
1.169 |
1.446 |
2.106 |
1.613 |
2.118 |
1.313 |
|
|
|
|
|
|
Параметры элементов проектируемого фильтра определяются путём соответствующего пересчёта параметров элементов ФПНЧ:
ФПНЧ |
ФНЧ |
Формула для пересчёта |
aν |
Lν |
aν R0 |
Lν= 2 f 0 |
||
aμ |
Cμ |
aμ |
|
|
Cμ= 2 f 0 R0 |
Где R0=R2.
Значения рассчитанных параметров элементов ФНЧ:
|
a1 |
L |
= |
a2 R0 |
|
|
a3 |
L |
= |
a4 R0 |
|
|
a5 |
L |
= |
a6 R0 |
|
||||
|
2 f 0 |
|
2 f 0 |
|
2 f 0 |
||||||||||||||||
C1= |
|
|
2 |
|
C3= |
|
|
4 |
|
C5= |
|
|
6 |
|
|||||||
2 f 0 R0 |
2 f 0 R0 |
2 f 0 R0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
C1=55.8715 |
L2=24.8798 |
C3=100.6547 |
L4=27.7532 |
C5=101.2283 |
L6=22.5914 |
||||||||||||||||
|
нФ |
|
мГн |
|
нФ |
|
мГн |
|
нФ |
|
мГн |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
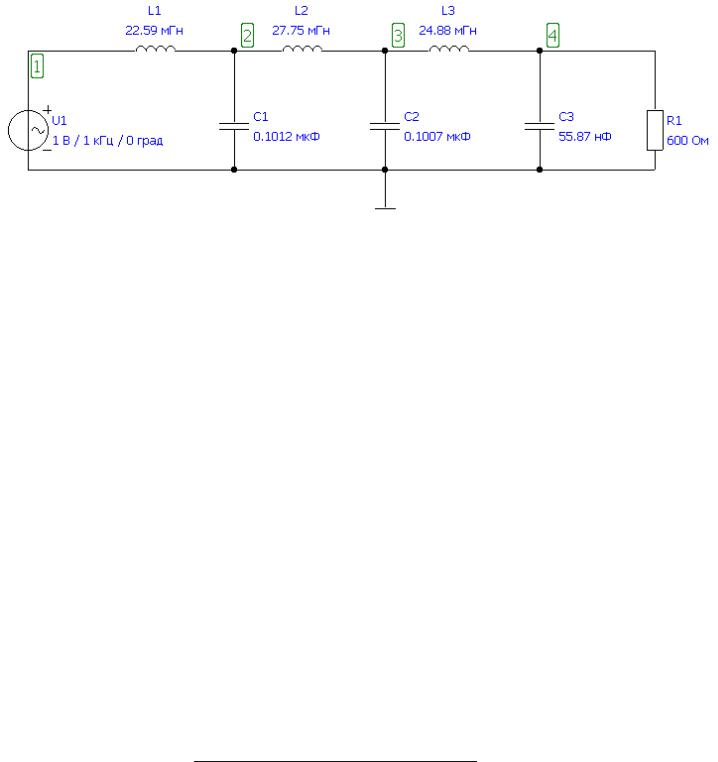
Схема ФНЧ имеет вид:
1.3 Определение передаточной функции фильтра
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
|
||
|
|
Передаточная функция полиномиального ФПНЧ: H p = |
|||||||
где |
|
V p |
|
|
|
|
|
V p |
|
|
- полином Гурвица 6-ой степени, B6 — коэффициент, определяющий |
||||||||
|
|
|
|
|
|
w=0 . |
|
|
|
величину ослабления фильтра на частоте |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Для ФПНЧ с характеристикой Чебышева при ∆a=1.25 дБ B6=0.05412 . |
|||||||
Сомножители полинома Гурвица имеют вид: |
|
|
|
||||||
V |
|
2 |
|
2 |
|
|
2 |
|
|
p = p |
0.4274 p 0.1158 |
p |
0.3128 p 0.5489 |
p 0.1144p 0.9817 |
|||||
Передаточная функция проектируемого фильтра H(p) находится частотным преобразованием передаточной функции H p фильтра-прототипа нижних частот.
Ниже приведена формула преобразования:
Передаточная функция |
Формула преобразования |
Передаточная функция ФНЧ |
|||||||||||||||
ФПНЧ |
|
|
|
|
|
|
|
|
H(p) |
|
|
|
|
||||
H p |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
p |
|
|
|
|
2 f 0 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
p= 2 f 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
2 f |
|
b |
|
p 2 f |
|
2 |
b |
||||||||
|
p b1 p b0 |
|
|
|
|
p |
0 |
1 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
Таким образом, передаточная функция ФНЧ H(p) имеет вид:
H p = |
|
97.32 1024 |
|
2 |
2 |
10907.861p 667481039.6879 |
|
|
p |
14904.1554 p 140816732.3663 p |
|
|
|
1 |
|
p2 3989.32 p 1193780536.8221
1.4 Расчёт характеристики ослабления проектируемого фильтра
Получим характеристику ослабления проектируемого фильтра частотным преобразованием характеристики ослабления ФПНЧ, которая при аппроксимации по Чебышеву имеет вид:
5
a w =10lg[ 100.1Δa−1 P2n w 1]
где n — порядок ФПНЧ; |
|
- нормированная частота ФПНЧ; |
P |
n |
w |
|
- полином |
||||||||
w |
|
|
|
||||||||||||
Чебышева n-ого порядка, определяющийся выражением (для n=6): |
|
|
|||||||||||||
|
6 |
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
P6 w =32w −48w 18w −1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для расчёта характеристики ослабления проектируемого фильтра a(f) можно |
||||||||||||||
использовать прямое преобразование частоты |
|
: |
w |
= |
f |
|
, подставляя его в |
||||||||
|
|||||||||||||||
w |
|
|
f 0 |
||||||||||||
формулу характеристики ослабления ФПНЧ. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Выберем частотный диапазон f min f f max |
, где fmin=0 Гц; fmax=1.2fk кГц. И число |
|||||||||||||
расчётных точек N=1000. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В результате получим график характеристики ослабления ФНЧ:
1.5 Моделирование фильтра на ПК
Моделирование фильтра на ПК выполнено в программе Fastmean. Ниже приведена схема рассчитанного фильтра:
6
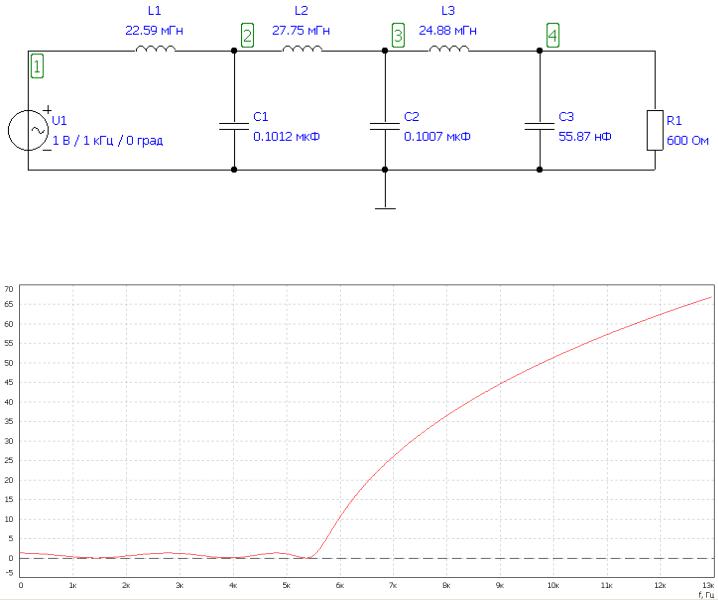
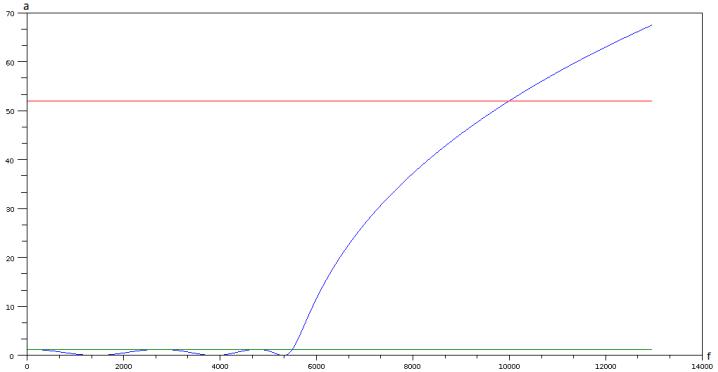
В программе получился следующий график характеристики ослабления:
2.Расчёт ARC-фильтра
2.1Содержание задания
Необходимо операторную передаточную функцию, полученную в задании 1, с точностью до постоянного множителя реализовать активной RC-цепью.
Врезультате решения требуется:
1)привести схему ARC-фильтра, составленную путём каскадного соединения звеньев. Обосновать выбор звеньев и порядок их включения в схеме фильтра;
2)рассчитать параметры элементов звеньев методом уравниванию коэффициентов;
7
3)получить выражения и построить графики АЧХ и ФЧХ, а также частотных зависимостей чувствительностей АЧХ и ФЧХ к изменению параметра заданного элемента wk;
4)рассчитать характеристику ослабления ARC-фильтра через его передаточную функцию либо путём моделирования фильтра на ПК;
5)сравнить графики характеристик ослабления LC и ARC-фильтров и сделать выводы.
2.2 Построение схемы
Схема ARC-фильтра составляется путём каскадно-развязанного соединения звеньев 2-ого и 1-ого порядка, каждое из которых реализует один из сомножителей функции H(p), полученной в задании 1:
Hi p = |
b0i |
; |
|
p2 a1i p a0i |
|||
|
|
Каскадно-развязанный принцип реализации обусловлен тем, что с повышением порядка передаточной функции фильтра резко увеличивается чувствительность его частотных и временных характеристик к изменению параметров элементов, а также повышается вероятность неустойчивой работы цепи. В связи с этим на практике, как правило, применяют ARC-звенья не выше 2-ого порядка.
Звенья следует выбирать так, чтобы вид их передаточной функции соответствовал типу фильтра. При выборе звеньев также следует учитывать величину добротности полюса сомножителя передаточной функции фильтра, рассчитываемой
по формуле Q= |
|
a0 |
. При Q<5 рекомендуется использовать звенья с одним |
|
a1 |
||||
|
|
|||
операционным усилителем. При реализации сомножителей с большими значениями добротностей следует использовать звенья, построенные по методу АВТ.
Рассчитаем добротности полюсов сомножителей H(p):
Q = |
|
|
Q = |
|
|
Q = |
|
|
|||
1.4082 108 |
6.6748 108 |
1.1938 109 |
|||||||||
1 |
1.4904 104 |
2 |
1.0908 104 |
3 |
|
3.989 103 |
|||||
|
|
|
|
||||||||
|
Q1=0.7962 |
|
Q2=2.3685 |
|
Q3=8.6609 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, в схеме фильтра необходимо использовать 2 звена с одним операционным усилителем и одно звено, построенное по методу АВТ.
ARC-звенья в схеме фильтра во избежание их перегрузки, появления нелинейных искажений и с целью улучшения соотношения сигнал/шум следует располагать от входа к выходу в порядке возрастания добротности полюса передачи.
2.2 Расчёт параметров элементов ARC-фильтра
Для нахождения численных значений параметров элементов выбранных звеньев составляется система уравнений путём уравнивания численных коэффициентов реализуемого сомножителя передаточной функции фильтра, полученной в задании 1, с соответствующими буквенными коэффициентами передаточной функции звена, выбранного из таблиц 2.1, 2.2.
8
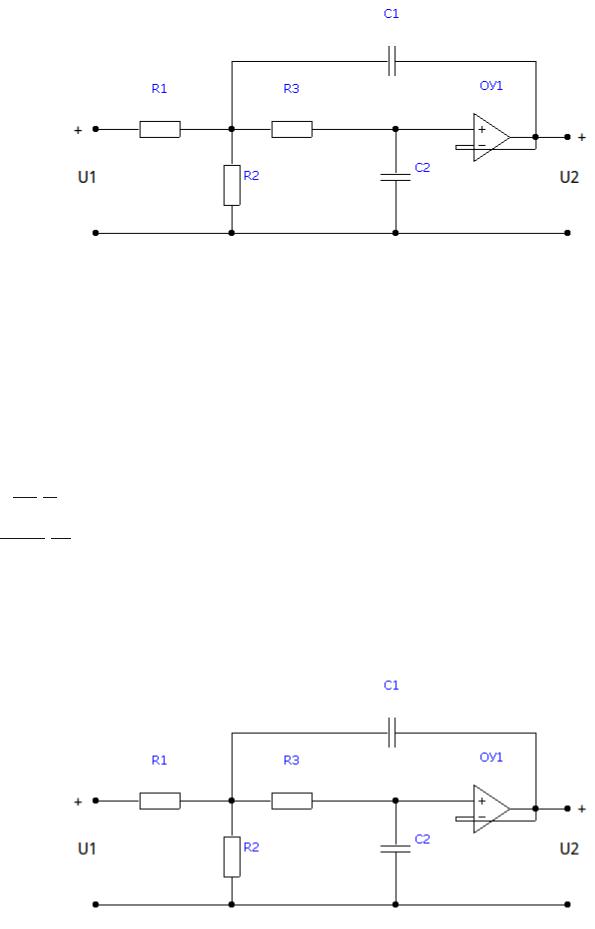
Звено №1, Q1=0.7962 (схема №1 из таблицы 2.1)
Операторная передаточная функция звена:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
H p = |
|
|
|
|
|
|
|
R1R3C1C2 |
|
|
|
|
|
|
|
|
|
|||
p2 |
1 |
|
1 |
|
1 |
|
1 |
p |
1 |
|
|
1 |
|
1 |
|
1 |
|
|||
|
|
|||||||||||||||||||
|
C1 |
R1 |
R2 |
R3 |
|
|
|
R2 |
R1 |
|||||||||||
|
|
|
|
|
|
|
C1C2 R3 |
|
|
|
||||||||||
Положим R1=R2=R3=R=70 кОм. Требуется рассчитать C1, C2.
Значения коэффициентов первого сомножителя передаточной функции, полученной в 1-ом задании: a1=1.4904 104 ;a0=1.4082 108 .
Составим систему уравнений:
C11 R3=1.4904 104
C1C21 R22 =1.4082 108
В результате получим: C1=2.8755 нФ; C2=1.008 Нф.
Звено №2, Q2=2.3685 (схема №1 из таблицы 2.1)
9
Операторная передаточная функция звена:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
H p = |
|
|
|
|
|
|
|
|
R1R3C1C2 |
|
|
|
|
|
|
|
|
|
|||
p2 |
1 |
|
1 |
|
|
1 |
|
1 |
p |
1 |
|
|
1 |
|
1 |
|
1 |
|
|||
|
|
|
|||||||||||||||||||
|
C1 |
R1 |
R2 |
R3 |
|
|
|
R2 |
R1 |
||||||||||||
|
|
|
|
|
|
|
C1C2 R3 |
|
|
|
|||||||||||
Положим R1=R2=R3=R=95 кОм. Требуется рассчитать C1, C2.
Значения коэффициентов первого сомножителя передаточной функции, полученной в 1-ом задании: a1=1.0907 104 ;a0=6.6748 108 .
Составим систему уравнений:
C11 R3=1.0907 104
C1C21 R22 =6.6748 108
В результате получим: C1=2.8951 нФ; C2=0.1147 нФ.
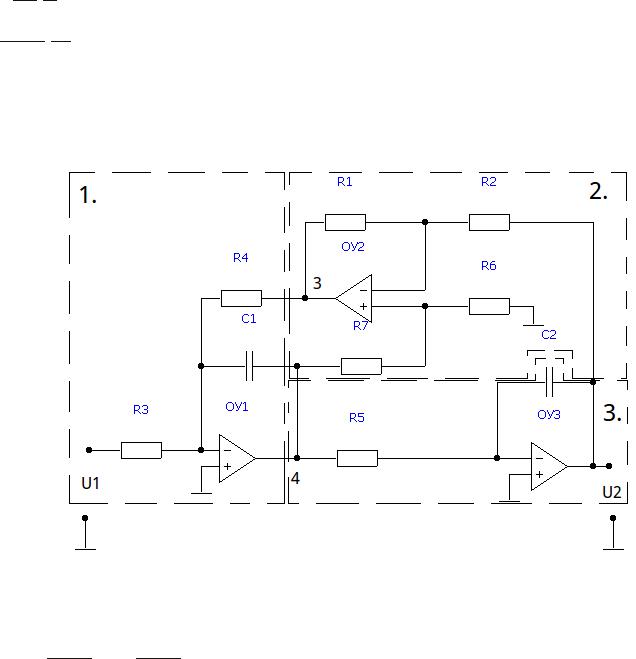
Звено №3, Q3=8.6609 (схема №7 из таблицы 2.2)
3-е звено составлено по методу АВТ. Оно содержит 3 операционных усилителя. Разобьём звено на 3 блока, содержащие по одному операционному усилителю:
1. интегратор-сумматор. cвязь между выходным и входным выражением определяется выражением:
U4=−C1R41 U3p − C1R31 U1p
2. алгебраический сумматор. cвязь между выходным и входным выражением определяется выражением:
10
