методичкаМОСС

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО СВЯЗИ И ИНФОРМАТИЗАЦИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

им. проф. М.А. БОНЧ-БРУЕВИЧА

Я.С. Дымарский МЕТОДЫ ОПТИМИЗАЦИИ

СЕТЕЙ СВЯЗИ Методические указания и контрольные задания

200900, 220200, 220400, 550400

Санкт-Петербург

2003

1

УДК 621.391.28

Дымарский Я.С. Методы Оптимизации сетей связи: Методические указания и контрольные задания. Для студентов специальностей 200900, 220200,

220400, 550400 / СПбГУТ. – СПб, 2003.

Рекомендовано к печати редакционно-издательским советом университета.

Приводятся теоретические основы, методы и алгоритмы решения оптимизационных задач, варианты контрольных заданий и указания (при необходимости) по их выполнению.

© Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича, 2003.

2

Общие положения

1. Оптимизационной задачей (ОЗ) называется кортеж

ОЗ=< f (x), X, Y>,

(1)

где f(x) – целевая функция, экстремумы которой необходимо найти, варьируя значения компонентов вектора (точки) x=(x1, x2, …, xn),

X– область определения f(x),

Y– область ограничений, накладываемых на вектор x.

Область D=X∩Y называется допустимой, вектор x D – допустимым вектором ОЗ. Если допустимое множество D совпадает с евклидовым пространством Rn, ОЗ называется задачей безусловной оптимизации.

2. Допустимый вектор x0 называется абсолютным (глобальным) минимумом, если

3. Допустимый вектор x0l называется локальным минимумом, если существует такое δ > 0, что при всех 0 ≤ | x|≤ δ справедливо

Для максимумов знак неравенства в (2) и (3) меняется на обратный.

4. Локальный минимум называется внутренним или граничным, если точка x0l является соответственно внутренней или граничной точкой области D. Например, функция f(x)=x при –∞<x<+∞ не имеет экстремумов, а f1(x)=x при x≤1 имеет в точке x=1 граничный максимум, а при 0≤x≤1 имеет еще и граничный минимум в точке x=0.

Справочная информация

Правила вычисления производных

1) ;

2)[Af(x)]'=Af '(x) – постоянный множитель можно выносить за знак производной;

3)f(x)=A; f '(x)=0 x;

4)f(x)=u(x)±v(x); f'=u' ± v'. Правило справедливо для любого числа слагаемых;

3

5) y=f(x)=u(x)·v(x); y'=u'v+uv'. Если y=uvw, то y'=u'vw+uv'w+uvw'. Для случая n

сомножителей – аналогично;

6) – формула Лейбница.

7)(предположение: v0);

8) производная от сложной функции

;

9) производная от обратной функции

x=g(y) – обратная функция для y= f(x); .

Пример 1. y=arcsin x. Обратная функция x=sin y,

;

10) производная от неявной функции

.

Для случая n переменных: F(x1, x2, …, xn, y)=0;

.

4

Производные основных элементарных функций

Таблица 1

Типичные функции нескольких переменных

Рассматриваются два класса функций нескольких переменных:

(4)

(5)

5

Пример 2. Целевая функция задачи распределения пропускных способностей Л. Клейнрока [1]:

где T – среднесетевая задержка сообщения;

j – интенсивность потока сообщений в j-м канале;

– средняя длина одного сообщения;

– суммарный трафик в системе;

C j– искомое значение пропускной способности j-го канала.

Необходимо найти производную целевой функции по C j. Имеем (по правилу(4)):

Пример 3. Целевая функция задачи распределения разнотипных каналов по направлениям связи [2]:

,

ij = - ln(1 - wij ),

где M – математическое ожидание числа надежно функционирующих направлений связи; n – количество направлений связи;

v j – коэффициент важности j-го направления связи;

wij – надежность одного канала i-го типа, функционирующего на j-м направлении связи;

m – количество типов каналов;

xij – искомое значение количества каналов i-го типа, выделенных на j-е направление связи.

6

Необходимо найти производную целевой функции по xij. Имеем (по правилу (5)):

Тема 1. Классическая оптимизация

1.1. Безусловная оптимизация

1.1.1. Функции одной переменной

Условия существования внутренних максимумов и минимумов следующие: если существует производная f '(a), то функция f(x) может иметь в точке a внутренний максимум или минимум лишь в том случае, когда

(необходимое условие экстремума).

Если существует вторая производная f ''(a), то функция f(x) имеет в точке а

минимум при f '(a)=0 и f ''(a)>0.

Более общее утверждение: если существует производная f(n)(a) и если f '(a)=f ''(a)=…=f (n– 1)(a)=0, то функция f (x) имеет в точке а

минимум при n четном и f (n)(a) >0.

Если n нечетно, то функция f (x) в точке а не имеет ни минимума, ни максимума, а имеет

точку перегиба.

Условия (1.2) и (1.3) являются достаточными условиями экстремума.

Если f '(a)=0, то во всех случаях говорят, что функция f (x) при x=a имеет стационарное значение, а точка x=a называется стационарной.

7

Пример 1.1. Каждая из функций x2, x4, x6, ... имеет при x=0 минимум, а каждая из функций x3, x5, x7, ...имеет x=0 точкой перегиба.

Более общим, чем (1.1)–(1.3), и зачастую более удобным является следующее правило: если производная f '(x) при переходе через стационарную точку а меняет

знак “–” на ”+”, то налицо минимум.

Если f '(x) знака не меняет, то экстремума нет.

Пример 1.2. Функция Коши f(x)=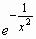 (f(0)=0) имеет при x=0 производные всех порядков, причем все они равны нулю. Хотя при x=0 эта функция имеет минимум, установить этот факт с помощью правила (1.3) невозможно. С помощью же правила (1.4) это удается сделать:

f '(x)=,

слева от нуля f '(x)<0, а справа – f '(x)>0.

По правилу (1.4) в точке x=0 функция f (x) обращается в минимум.

Пример 1.3. Найти экстремумы функции f(x) = x3(x2 - 1) при –1≤x≤2.

Необходимое условие оптимальности:

f '(x)=5x4 - 3x2 = x2(5x2 - 3) = 0.

Корни этого уравнения: х=0, . Присоединяя к ним граничные значения х= -1 и х=2, получаем пять стационарных точек:

x1 = - 1,x2 = - 0,775, x3 = 0, x4 = 0,775, x5 = 2.

Поскольку f '(x1) >0 и f '(x5) >0, в точке x1 – граничный минимум, в точке x5 – граничный максимум. Далее, в точке x2 вторая производная

следовательно, это точка локального максимума, в точке x4 производная f ''(x4) = 4,66>0, значит, это точка локального минимума. Наконец,f ''(x3) =0, f

'''(x3) 0. Поскольку номер отличной от нуля производной – нечетное число, в точке x3 экстремума нет, здесь – перегиб.

1.1.2. Унимодальные функции одной переменной

Унимодальной называется функция, имеющая на заданном отрезке [a,b] один максимум или минимум. Использование свойства унимодальности позволяет построить эффективные методы локализации экстремума – методы золотого сечения и чисел

8

Фибоначчи. Обоснование и описание методов приведено в работах [2, 3]. Здесь рассматриваются только алгоритмы.

Алгоритм 1 (поиска экстремума унимодальной функции f (x) на отрезке [a, b] методом золотого сечения)

1.Ввести исходные данные (ИД): a, b, необходимая точность локализации экстремума ε, адрес процедуры вычисления f (x), признак

2.Вычислить

3.Выполнить присвоения а1:=а, а2:=b, i:=1.

8.Вычислить d=δ(y1–y2).

9.Проверить выполнение условия а2–а1≤ε. Если оно выполняется, то перейти к п. 14, если нет – к п. 10.

10.Выполнить присвоение i:=i+1.

11.Проверить выполнение условия d>0. Если условие выполняется, то перейти к п. 12, если нет – к п. 13.

12.Положить а2:=х2, у2:=у1, х2:=х1, выполнить процедуры 1.1 и 2.1, и перейти к п.8.

13.Положить а1:=х1, у1:=у2, х1:=х2, выполнить процедуры 1.2 и 2.2, и перейти к п.8.

14.Print (a1, a2, y1, y2, i).

15.End

Алгоритм 2 (поиска экстремума унимодальной функции f (x) на отрезке [a, b] методом чисел Фибоначчи)

1.Действия такие же, как в п. 1 алгоритма 1.

2.Выполнить присвоения а1:=а, а2:=b.

3.Вычислить и .

4.Вычислить

9

где E(x) – целая часть х; {x} – дробная часть х.

10.Выполнить присвоение i:=1.

11.Вычислить d=δ(y1–y2) и выполнить присвоения D:=B, C:=B–A, B:=A, A:=C.

12. . Проверить выполнение условия d>0. Если условие выполняется, перейти к п.13, если нет – к п. 14.

13.Действия такие же, как в п. 12 алгоритма 1. Перейти к п. 15.

14.Действия такие же, как в п. 13 алгоритма 1. Перейти к п. 15.

15.Выполнить присвоение i:=i+1.

16.Проверить выполнение условия i=n. Если условие не выполняется, перейти к п.11, если выполняется – к п. 17.

17.Print (a1, a2, y1, y2, n).

18.End.

1.1.3. Функции нескольких переменных [4]

Необходимые условия оптимальности следующие: если функция f (x1, x2, …, xn) дифференцируема в точке а=(а1, а2, …, аn), то она может иметь в этой точке внутренний максимум или минимум лишь в том случае, когда ее первый дифференциал df обращается в этой точке в нуль, т.е. когда

Достаточные условия оптимальности: если функция f имеет в точке а непрерывные вторые частные производные и если в этой точке выполняются необходимые условия (1.5), то в случае, когда второй дифференциал

10