методичкаМОСС

, следовательно, в соответствии с (2.5) W j (x j)– вогнутая функция;

функция M(x)имеет структуру (2.4), предусмотренную утверждением 1, следовательно, M(x)– вогнутая функция;

ограничения (2.12), (2.13) задают выпуклое множество.

Функция Лагранжа, формируемая по правилу (2.8), выглядит так:

. (2.15)

Необходимые и достаточные условия оптимальности по ОТПМ следующие:

(2.16)

Из (2.16) получаем

(2.17)

где

Анализируя верхнюю и нижнюю ветви (2.17), приходим к такой эквивалентной форме условий оптимальности:

21

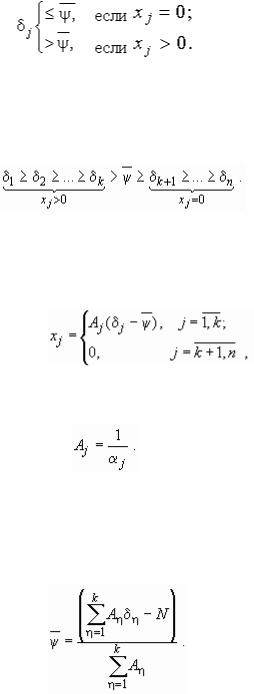
Это означает, что параметр делит множество значений j на два подмножества, что наглядно иллюстрирует рассмотрение вариационного ряда (2.20), построенного по невозрастанию (убыванию) величин j :

(2.20)

Для каждого из направлений связи левого подмножества, выполняется нижняя ветвь условий (2.19), поэтому здесь x j> 0, правого подмножества – верхняя ветвь, поэтому здесь x j= 0. Из (2.20) и (2.17) следует

(2.21)

где

Необходимо отметить, что в (2.21) используется новая нумерация направлений связи, отвечающая расположению величин j в вариационном ряду (2.20).

Из (2.12) и (2.21) находим:

(2.22)

Величина k находится с помощью итерационного процесса, в котором для последовательных значений k = 1,2,... проверяется выполнение условий (2.19).

Изложенные соображения делают понятным следующий алгоритм решения задачи (2.11)–

(2.13).

Алгоритм 3 (оптимального нецелочисленного распределения каналов по направлениям связи)

1. Ввести исходные данные: скаляры n и N; векторы v j, w j, j = 1,2,..., n. Значение n– целое, остальные величины – вещественные числа, большие нуля.

22

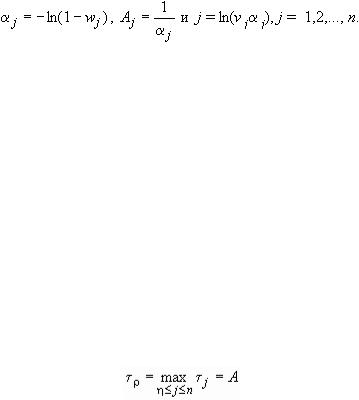
2.Вычислить значения

3.Положить := 1

4.Положить j := j , j := 1, j = 1,2,..., n.

5.Положить A := , j := , p :=

6.Проверить выполнение условия j - A > 0. Если условие выполняется, то перейти к п. 7, если нет – то к п. 8.

7.Положить A := j , := j

8.Положить j := j + 1.

9.Проверить выполнение условия j n. Если условие выполняется, то перейти к п.10, если нет – то к п. 6. (Сomment – в пп.5–9 находится

(2.23)

и фиксируется значение индекса . )

10. Положить

a := , := A, := a, b := A , a := , := p, := a.

11.Положить := + 1.

12.Проверить выполнение условия n Если условие выполняется, то перейти к п.5, если нет – то к п.13. (Сomment – в пп. 3–12 осуществляется построение вариационного ряда

в массиве {j }и упорядоченной в соответствии с расположением величин j в этом ряду последовательности величин Aj – в массиве {j}. В массиве { j} содержатся старые номера направлений связи. Фактически в пп. 3–12 осуществляется операция сортировки массива чисел по одному из возможных алгоритмов. В принципе, могут быть использованы и другие алгоритмы сортировки.)

13 Положить k := 1

14. Вычислить

23

15.Проверить выполнение условия k k 1. Если условие выполняется, то перейти к п.18, если нет – то к п.16.

16.Проверить выполнение условия k= n - 1. Если условие выполняется, то положить k:= n, вычислить значение

и перейти к п. 18. Если же условие не выполняется, то перейти к п. 17.

17.Положить k:= k + 1 и перейти к п. 14. (Сomment – в пп. 13–17 вычисляются значения k

и k)

18.Вычислить значения компонентов оптимального решения по формуле

19.Перейти к исходной нумерации направлений связи, для чего положить a := j , xa:= y j , j = 1,2, ...n

20.Print

21.End.

24

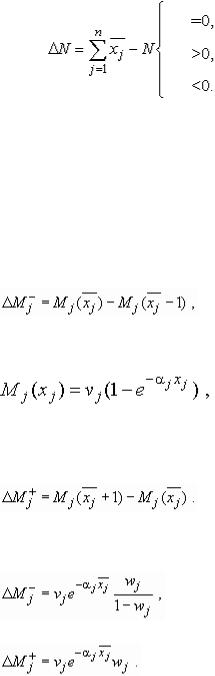
Пример 2.1. Исходные данные и результаты вычислений приведены в табл. 9.

Алгоритм 3 дает оптимальное нецелочисленное решение x = {x j} Для практического

использования необходимо округлить компоненты x j до целых значений по тому или иному правилу. В результате округления могут встретиться три случая:

(2.25)

Действительно, как показывают данные табл. 9, для N =2,5, 8 и 15 имеет место случай N = 0 , при N = 12 - N <0, при N = 20 - N>0. В первом случае можно считать

целочисленное решение оптимальным. Во втором необходимо “снять” N каналов с тех или иных направлений связи, чтобы добиться выполнения директивного условия (2.12). В третьем необходимо для достижения той же цели дораспределить N каналов. Снятие целесообразно осуществлять по одному каналу так, чтобы на каждом из N шагов убывание эффективности

(2.26)

где

(2.27)

было минимальным. Добавление каналов целесообразно осуществлять на такие направления связи, где обеспечивается максимальное приращение эффективности

(2.28)

Можно показать, что

(2.29)

(2.30)

Приведенные соображения реализованы в алгоритме 4.

Алгоритм 4 (оптимального целочисленного распределения каналов по направлениям связи)

26

1.Ввести ИД: скаляры n и N, векторы v j и

2.–12. Действия такие же,как в пп. 2–12 алгоритма 3.1.

13.Вычислить и отпечатать значения по формуле

14.Проверить выполнение условия N >Yn. Если условие выполняется, то положить k := n и перейти к п.16 ; в противном случае – к п.15.

15.Найти значение индекса k из условия

Y k<

16.Вычислить

17.Вычислить компоненты оптимального плана по соотношению

18.Перейти к прежней нумерации направлений связи () и округлить значения x j по правилу Гаусса:

19.Найти и

20.Проверить выполнение условия N = 0 Если условие выполняется, то перейти к п. 24, если нет – то к п. 21.

21.Проверить выполнение условия N >0. Если условие выполняется, то перейти к п. 22, если нет – то к п. 23.

27

22. Найти значение индекса s из соотношения

выполнить присвоения и перейти к п. 20.

23. Найти значение индекса r из соотношения

,

выполнить присвоения и перейти к п. 20.

24. Print

.

25. End.

Пример 2.2. Исходные данные – те же, что и в примере 2.1.

Результаты вычислений для двух критичных значений N=12 (необходимо дораспределить один канал) и N =20 (необходимо снять один канал) приведены в табл. 10.

Из данных табл. 10 видно, что в первом случае необходимо добавить один канал на первое (или четвертое) направление связи, где приращение эффективности максимально, во втором – снять один канал со второго направления, где уменьшение эффективности минимально.

28

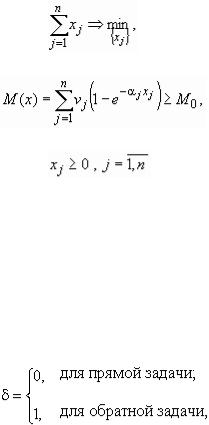
Непосредственно оптимальное целочисленное решение, минуя этап отыскания нецелочисленного решения, можно получить методом максимального элемента (ММЭ), являющегося обобщением используемого в алгоритме 4 метода дораспределения каналов. В основе ММЭ лежат два фундаментальных положения:

1)каналы (ресурсы) распределяются пошагово, по одному (по единице ресурса), начиная с нулевого состояния, когда ни на одно из направлений связи не выделено ни одного канала;

2)на каждом шаге канал назначается на то направление связи, где достигается максимальное приращение эффективности.

Важной является классификация оптимизационных задач на прямые и обратные. Прямые

– это задачи анализа, определения максимально достижимого при данном ресурсе значения эффективности системы. Обратные – задачи синтеза, определения минимального ресурса, при котором достигается заданное значение эффективности системы. Рассмотренная выше задача (2.11)–(2.13) относится к классу прямых. Примером обратной может служить задача в такой постановке:

(2.31)

Отличительной особенностью ММЭ является возможность его использования для решения как прямой, так и обратной оптимизационной задачи. Это непосредственно следует из приводимого далее алгоритма 5.

Алгоритм 5 (решения прямой и обратной задач оптимального целочисленного распределения каналов по направлениям связи ММЭ)

1. Ввести ИД: n, признак класса решаемой задачи

векторы v j,

29

и проверить выполнение условия F<D.

Если условие выполняется, перейти к п. 3, если нет – к п. 7.

7.Print (M, L, {x j}).

8.End.

Пример 2.3. Исходные данные те же, что и в примере 2.1. Результаты решения по алгоритму 5 приведены в табл.11.

30