tvims_3

Заметим, что fX,Y (x, y) 6≡fX (x) fY (y), т. е. случайные величины X и Y зависимы.

4) Найдем математическое ожидание

иcov (X, Y) = E(XY) − EX EY = 158 − 45 · 45 = − 758 .

7)Коэффициент корреляции

81

y

1 D pπ/2

0

x

Рис. 2.10. Область D из задачи 12.2.

12.2. Пусть случайный вектор (X, Y) имеет равномерное распределение в круге D : x2 + y2 6 π2 . Найти плотность и математическое ожидание случайной величины Z = sin X2 + Y2 .

2

=

0, z / (0, 1) .

Математическое ожидание

82

Можно найти EZ по другой формуле, используя плотность fX,Y (x, y):

12.3. Пусть случайные величины X и Y независимы и имеют стандартное нормальное распределение. Найти плотность случайной величины Z = X2 + Y2.

Решение. Так как X и Y независимы, то совместная плотность их распределения имеет вид

Таким образом, величина Z = X2 + Y2 имеет показательное распределение. 12.4. Пусть случайные величины X и Y независимы и имеют показательное

распределение с одним и тем же параметром λ > 0. Найти плотность распределения случайной величины Z = X + Y.

Решение. Плотности распределения случайных величин X и Y имеют вид

83

Так как Z = X + Y > 0, то fZ (z) = 0 при z < 0. Рассмотрим случай z > 0. В этом

случае

∞

Z

fZ (z) = fX (x) fY (z − x) dx.

−∞

Подынтегральное выражение отлично от 0 при x > 0, z − x > 0, т. е. 0 6 x 6 z. Следовательно,

12.5. Пусть случайные величины X и Y независимы и имеют равномерное распределение на отрезках [0, 1] и [1, 2] соответственно. Найти плотность распределения случайной величины Z = X + Y.

Решение. Плотности распределения случайных величин X и Y имеют вид

Так как 0 6 X 6 1, 1 6 Y 6 2, то 1 6 Z = X + Y 6 3, и fZ (z) = 0 при z / [1, 3]. Рассмотрим случай z (1, 3). В этом случае

∞

Z

fZ (z) = fX (x) fY (z − x) dx.

−∞

Подынтегральное выражение отлично от 0 при 0 6 x 6 1, 1 6 z − x 6 2, т. е. 0 6 x 6 1 и z − 2 6 x 6 z − 1. Следовательно,

z − 1. Если 2 6 z < 3, то max{0, z − 2} = z − 2, min{1, z − 1} = 1, и fZ (z) =

84

y

1

x

0 1 3

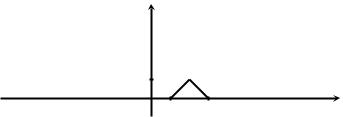
Рис. 2.11. Плотность fZ(z) из задачи 12.5.

1

Z

dx = 3 − z. Таким образом,

z−2

z − 1, 1 < z 6 2;

fZ (z) = 3 − z, 2 6 z < 3;

0, z / [1, 3].

12.6.Случайный вектор (X, Y) имеет равномерное распределение в прямоугольнике с вершинами (−1, 0), (0, −1), (1, 0), (0, 1). Найти частные распределения и проверить, являются ли X, Y независимыми.

12.7.Случайный вектор (X, Y) имеет равномерное распределение в прямоугольнике с вершинами (−1, −1), (1, −1), (1, 1), (−1, 1). Найти частные распределения

ипроверить, являются ли X, Y независимыми.

12.8.Случайный вектор (X, Y) имеет равномерное распределение в треугольнике с вершинами (1, 0), (0, 1), (−1, 0). Найти частные распределения и проверить, являются ли X, Y независимыми. Найти EX, EY, DX, DY, cov (X, Y), ρ (X, Y).

12.9.Случайный вектор (X, Y) равномерно распределен в треугольнике D с вершинами A1 (0, 0), A2 (0, 4), A3 (−2, 0). Найти плотность совместного распределения случайных величин X и Y, вероятность P (X 6 −1, Y > 1), одномерные

плотности и функции распределения случайных величин X и Y. Найти EX, DX,

EY, DY, cov (X, Y), ρ (X, Y).

12.10. Задана плотность совместного распределения случайных величин X и

85

Y:

где D — прямоугольник, задаваемый неравенствами 0 6 x 6 1, −4 6 y 6 0. Найти коэффициент C, вероятность P (X > 0, Y > −1) и одномерные плотности распределения случайных величин X и Y. Найти EX, DX, EY, DY, cov (X, Y), ρ (X, Y).

12.11. Задана плотность совместного распределения случайных величин X и

где D — прямоугольник, задаваемый неравенствами −1 6 x 6 1, 0 6 y 6 5. Найти коэффициент C, вероятность P (X 6 0, Y > 2) и одномерные плотности распределения случайных величин X и Y. Найти EX, DX, EY, DY, cov (X, Y), ρ (X, Y).

12.12. Задана плотность совместного распределения случайных величин X и

где D — прямоугольник, задаваемый неравенствами 0 6 x 6 π, 0 6 y 6 π. Найти коэффициент C, вероятность P X 6 π2 , π4 6 Y 6 34π и одномерные плотности распределения случайных величин X и Y. Найти EX, DX, EY, DY, cov (X, Y),

ρ(X, Y).

12.13.Случайные величины X1, X2, . . . , Xn независимы и имеют одинаковые распределения с плотностью

Найти плотность распределения случайной величины Y = min (X1, X2, . . ., Xn).

12.14.Случайные величины X и Y независимы и X = E (α), Y = E (α). Найти

3 .функцию

12.15. Случайная величина X равномерно распределена на отрезке [0, 1], случайная величина Y равномерно распределена на отрезке [0, 4]. Известно, что X и Y — независимые случайные величины. Найти функцию распределения случайной величины Z = XY.

86

12.16.Случайная величина X равномерно распределена на отрезке [5, 9], случайная величина Y равномерно распределена на отрезке [3, 6]. Известно, что X и Y — независимые случайные величины. Найти плотность распределения случайной величины Z = X + Y.

12.17.Незавимимые случайные величины X и Y заданы плотностями распре-

делений:

Найти плотность распределения случайной величины Z = X + Y.

12.18. Незавимимые нормально распределенные случайные величины X и Y заданы плотностями распределений:

Найти плотность распределения случайной величины Z = X + Y, убедиться, что величина Z имеет нормальное распределение.

12.19. Пусть случайные величины X и Y независимы и каждая имеет равномерное распределение на отрезке [0, 2]. Найти функции распределения и плотно-

2.5Предельные теоремы

Пусть имеется последовательность независимых одинаково распределенных случайных величин X1, X2, . . ., Xn, . . .. Составим среднее арифметическое n первых слагаемых: 1n (X1 + . . . + Xn). Оказывается, что при больших n эта величина ведет себя не как случайная и приближается к математическому ожиданию каждого слагаемого. Это факт носит название закона больших чисел (ЗБЧ). Закон больших

87

чисел — это совокупность теорем. Доказательство теорем опирается на неравенство Чебышёва: пусть EX2 < ∞, тогда для любого ε > 0 справедливо неравенство

оно дает тривиальную оценку. Следует заметить, что оценка вероятности по неравенству Чебышёва несколько грубовата. Рассмотрим на примерах.

Задачи.

13.1. Пусть X = N (0, 1). Оценить снизу вероятности событий

A = {−3 < X < 3}, B = {−1 < X < 1}.

Решение. Так как X = N (0, 1), то EX = 0, DX = 1. Воспользуемся неравенством

(2.5.2):

P (−3 < X < 3) = P (|X − 0| < 3) > 1 − 19 = 89 .

Так как по условию распределение случайной величины известно, мы можем точно вычислить

P (|X| < 3) = Φ0,1 (3) − Φ0,1 (−3) = 2Φ0,1 (3) − 1 ≈ 0, 9974.

Оценим вероятность события B, используя неравенство (2.5.2):

P (|X| < 1) > 1 − 11 = 0.

Получили тривиальную оценку (почему?). А теперь вычислим точно:

P (|X| < 1) = 2Φ0,1 (1) − 1 ≈ 0, 6826.

13.2. Пусть известны числовые характеристики случайной величины X: EX = 0, 5; DX = 0, 1. Оценить снизу вероятности следующих событий:

A = {0, 1 < X < 0, 9}, B = {X < 1}.

88

Решение.

P (0, 1 < X < 0, 9) = P (−0, 4 < X − 0, 5 < 0, 4) =

роятностью 0, 01 лампочка имеет дефект нити накала и независимо от этого с вероятностью 0, 03 дефект цоколя. В каких границах будет практически наверняка заключено число бракованных лампочек? За вероятность практической достоверности принять 0, 95.

Решение. Пусть νn — количество бракованных лампочек, νn = Bi (n, p). Найдем p — вероятность, что лампочка оказывается бракованной: p = 0, 01 · 0, 97 + 0, 99 · 0, 03 + 0, 01 · 0, 03 ≈ 0, 04. Тогда Eνn = np = 1000 · 0, 04 = 40, Dνn = npq =

1000 · 0, 04 · 0, 96 = 38, 4. Воспользуемся неравенством Чебышёва (2.5.2):

P (|νn − Eνn| < ε) = 1 − P (|νn − Eνn| > ε) > 1 − Dεν2n > 0, 95.

Теперь остается решить неравенство 1 − Dεν2n > 0, 95, т. е. 1 − 38,ε24 > 0, 95. Получим

ε2 > 38, 4 = 153, 6, т. е. ε > 13. Таким образом, |νn − 40| < 13, т. е. 27 < νn < 53.

0, 25

13.4. Суточный расход воды в типовом девятиэтажном доме составляет в среднем 1200 кубометров. Оценить вероятность того, что в ближайшие сутки расход воды не превысит 3000 кубометров.

Решение. Обозначим через X суточный расход воды. По условию EX = 1200. Так как случайная величина X > 0, то применим неравенство Маркова (2.5.3)

P (X > ε) 6 P (X > ε) 6 EεX ,

P (X > 3000) 6 P (X > 3000) 6 12003000 .

Тогда P (X 6 3000) = 1 − P (X > 3000) > 1 − 0, 4 = 0, 6, т. е. искомая вероятность не меньше, чем 0, 6.

89

2.5.1 Закон больших чисел

Рассмотрим последовательность случайных величин {Xn}∞n=1 и случайную величину X, заданные на одном вероятностном пространстве (Ω, F , P).

Определение. Последовательность {Xn} сходится по вероятности к случайной величине X, если для любого ε > 0

P (|Xn − X| > ε) → 0 при n → ∞.

Обозначается сходимость по вероятности так:

P

Xn → X, n → ∞.

К законам больших чисел относятся следующие теоремы:

Tеорема 2.5.1 (Чебышёва). Пусть X1, X2, . . ., Xn — последовательность неза-

висимых и одинаково распределенных случайных величин с EX1 = a и конечной

n

дисперсией DX1 = σ2, Sn = P Xi. Тогда для любого ε > 0 имеет место неравен-

i=1

Tеорема 2.5.2 (Бернулли). Пусть νn — число «успехов» в n независимых испытаниях Бернулли, p — вероятность «успеха» в каждом испытании. Тогда для

Теорему 2.5.1 можно сформулировать и не для одинаково распределенных слагаемых:

Tеорема 2.5.3. Пусть X1, X2, . . ., Xn, . . . независимы и имеют конечные момен-

90