Связность

Пусть G – неориентированный граф. Маршрутом в G называется такая конечная или бесконечная последовательность ребер

, (1)

что каждые два соседних ребра иимеют общую концевую точку. Таким образом, можно записать

. (2)

Одно и то же ребро а может встретиться в маршруте несколько раз. Если в (1) нет ребер, предшествующих , тоназываетсяначальной вершиной S, а если нет ребер, следующих за , тоназываетсяконечной вершиной S. Любая вершина в (2), принадлежащая двум соседним ребрами, называетсявнутренней, или промежуточной, вершиной. Маршрут называется нетривиальным, если он содержит хотя бы одно ребро.

Если маршрут S имеет как начальную вершину , так и конечную вершину, то можно записать

(3)

и называть иконцевыми точками или концами маршрута S. Будем говорить, что S есть маршрут длины n, соединяющий и. Если, то маршрут будет называтьсяциклическим.

Маршрут называется цепью, а циклический маршрут – циклом, если каждое его ребро встречается в нем не более одного раза; вершины в цепи могут повторяться и несколько раз. Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется. Цикл с концом называетсяпростым циклом, если не является в нем промежуточной вершиной и никакие другие вершины не повторяются.

Теорема 3. Для того чтобы граф G представлял собой простой цикл, необходимо и достаточно, чтобы каждая его вершина имела степень 2.

Для ориентированного графа можно вводить как неориентированные маршруты, цепи и простые цепи, не принимая во внимание ориентации ребер, так и ориентированные маршруты (цепи, простые цепи), в которых все ребра (2) проходятся в направлении их ориентации. Ориентированную цепь называют также путем, а ориентированный цикл – контуром.

Пусть граф G – неориентированный. Две вершины иназываютсясвязанными, если существует маршрут вида (1) с концами и. Граф называетсясвязным, если любая пара вершин связана. В противном случае он является несвязным. Любой несвязный граф является совокупностью связных графов, которые обладают тем свойством, что никакая вершина одного из них не связана путем ни с какой вершиной другого. Каждый из этих графов называется компонентой графа G.

Пусть G – связный неориентированный граф. Так как две любые вершины исвязаны, существуют простые цепис концамии. Длины этих простых цепей являются неотрицательными числами. Следовательно, междуидолжны существовать цепи наименьшей длины. Эта наименьшая длина называетсярасстоянием междуи. Допустим, по определению,= 0. Для конечных связных графов можно также ввестипротяженность между двумя вершинами икак длину самой длинной связывающей их простой цепи.

Подграфы

Граф называетсяподграфом графа , еслииявляются подмножествамиR и , причем ребро содержится втолько в том случае, если его концевые вершины содержатся в.

Пусть–некоторое подмножество множества вершин графаи пусть– множество всех ребер графаG, концевые вершины которых входят в . Тогда графназываетсявершинно-порожденным подграфом графа G. Обозначим через некоторое подмножество множества ребер графаG и пусть есть множество всех вершин графаG, инцидентных ребрам из . Тогда графназываетсяреберно-порожденным подграфом графа G.

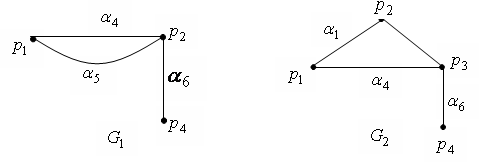
Рисунок 3.

На рис. 3 изображены вершинно-порожденный подграф , представленного на рис. 11.1 (множество вершин), и реберно–порожденный подграфтого же графаG (того же графа G ( множество ребер ).