Ответы на вопросы 1

2

Контрольные вопросы к ЛР01

1. Дайте определение дискретного и цифрового сигналов.

Дискретный сигнал — это сигнал, дискретный по времени и непрерывный по состоянию (уровню).

Цифровой сигнал — это сигнал, дискретный по времени и квантованный по состоянию.

2. Что такое период и частота дискретизации и как они связаны друг с другом?

 — период дискретизации (интервал между двумя соседними отсчетами)

3. Дайте определение дискретного и дискретного нормированного времени.

Значения называют дискретным временем (время n-ого отсчета), а  — дискретное нормированное время (тождественно ): .

4. Запишите аналитическую формулу цифрового единичного импульса и поясните смысл его фильтрующего свойства.

Фильтрующее свойство цифрового единичного импульса

Фильтрующее свойство означает, что из бесконечной последовательности выделяется один отсчет в момент времени .

5. Запишите аналитическую формулу дискретной экспоненты.

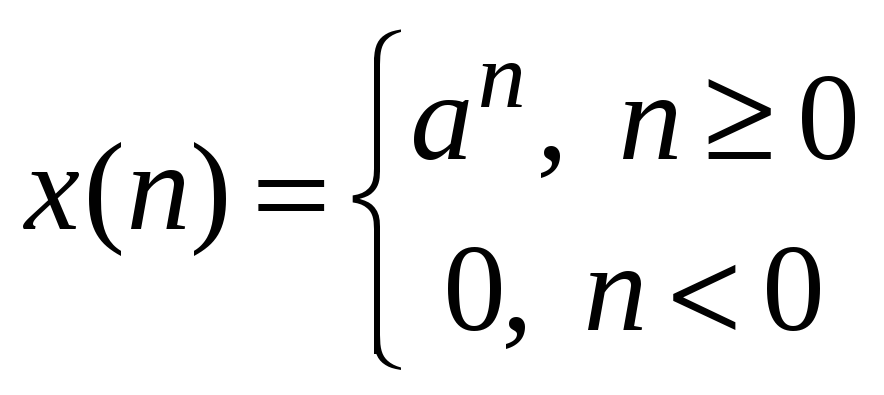
6. Запишите аналитическую формулу дискретного гармонического сигнала, вещественного и комплексного.

Дискретный гармонический сигнал

Дискретный комплексный гармонический сигнал:

Физически — это два сигнала:

.

7. Дайте определение нормированной частоты и поясните, как она отображается на комплексной z-плоскости.

нормированная частота – абсолютная частота, нормированная к частоте дискретизации:

Нормированная круговая частота:

Единицы измерения:

(Гц) (безразмерная);

( рад/с) (рад).

8. Дайте определение равномерного белого шума.

равномерный белый шум — последовательность случайных чисел в диапазоне от 0 до 1, распределенных равномерно, с заданными математическим ожиданием и дисперсией.

9. Дайте определение нормального белого шума.

нормальный белый шум — последовательность случайных чисел, распределенных по нормальному закону, с заданными математическим ожиданием и дисперсией.

10. Дайте определение АКФ и поясните ее вид.

Автокорреляционная функция (АКФ) конечной последовательности длины , позволяющая оценить зависимость между отсчетами последовательности в различные моменты времени , вычисляется по формуле:

;

где  — четная функция длины , центрированная относительно :

;

При этом в точке имеем:

;

где ,  — средняя мощность, математическое ожидание и дисперсия последовательности .

11. Для каких последовательностей, и с какой целью строится гистограмма?

Для последовательностей случайных чисел.