
- •1. Матрицы и действия с матрицами
- •2. Определители
- •3. Обратная матрица. Решение матричных уравнений
- •4. Ранг матрицы
- •5. Системы линейных уравнений. Основные понятия
- •6. Решение линейных систем по формулам Крамера
- •7. Решение систем с помощью обратной матрицы
- •8. Исследование систем линейных уравнений. Метод Гаусса
- •Индивидуальное задание
- •Приложение 1 Действия с матрицами на компьютере в excel.
Индивидуальное задание
Каждый студент выполняет задание при
конкретных значениях
![]() и
и![]() ,
которые определяются по номеру в журнале
группы:
,
которые определяются по номеру в журнале
группы:![]() −первая
цифра номера по списку,
−первая
цифра номера по списку,![]() −
вторая. Если номер по списку однозначный
−
вторая. Если номер по списку однозначный![]() .
.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
№ |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1.Вычислить определители:
![]() ,
,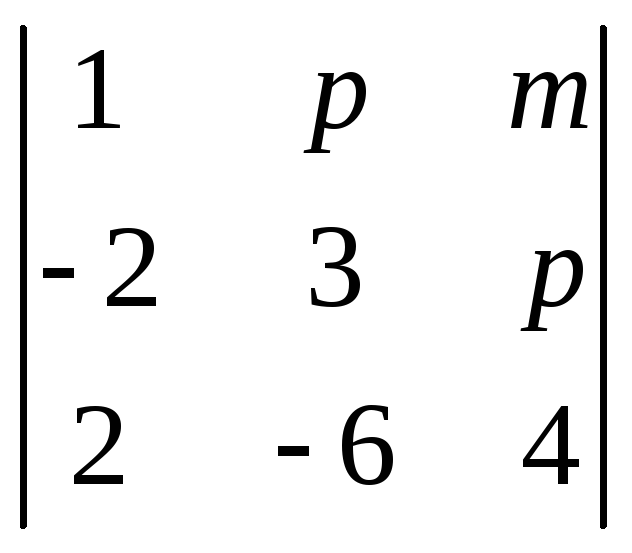 ,
,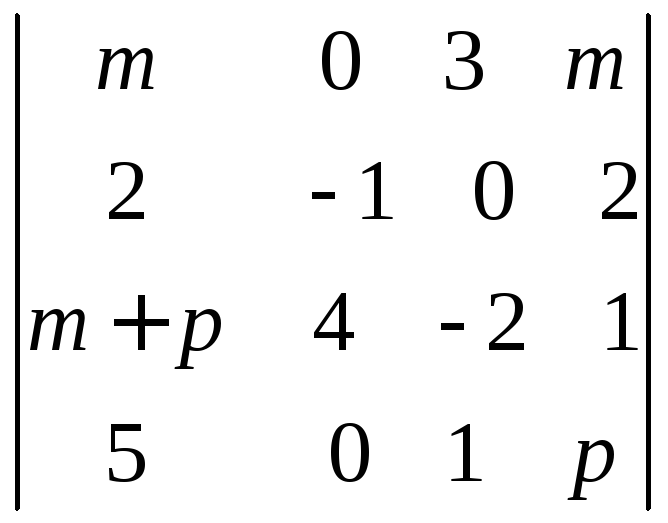 .
.
2.Даны матрицы:
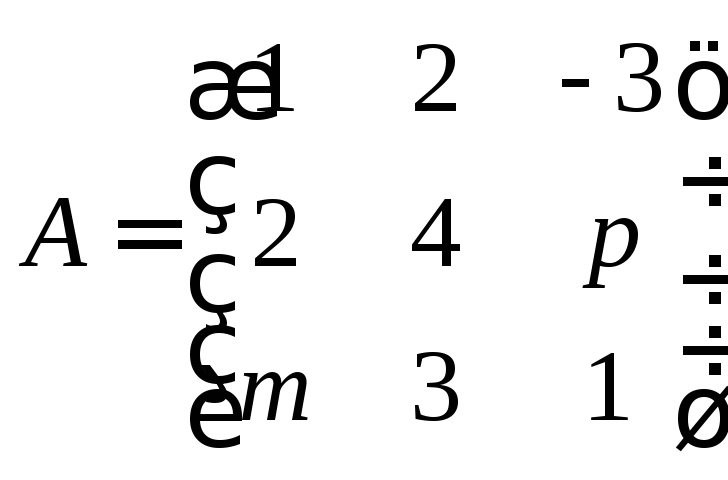 ,
,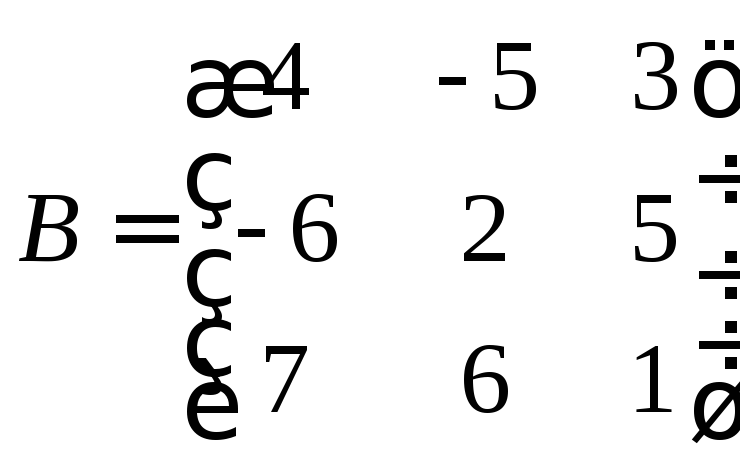 ,
,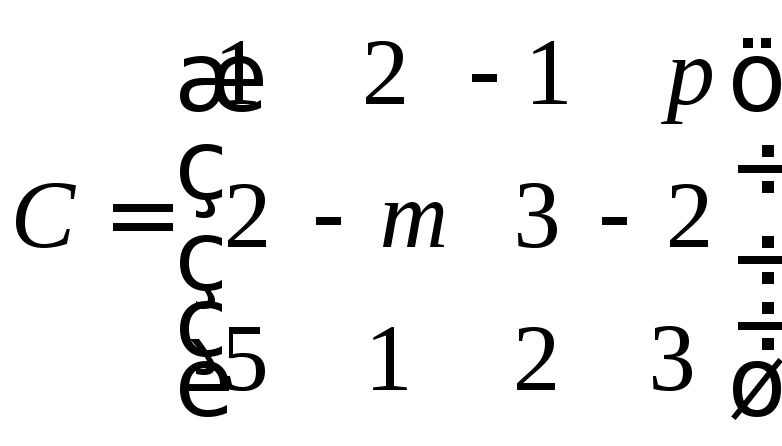 ,
,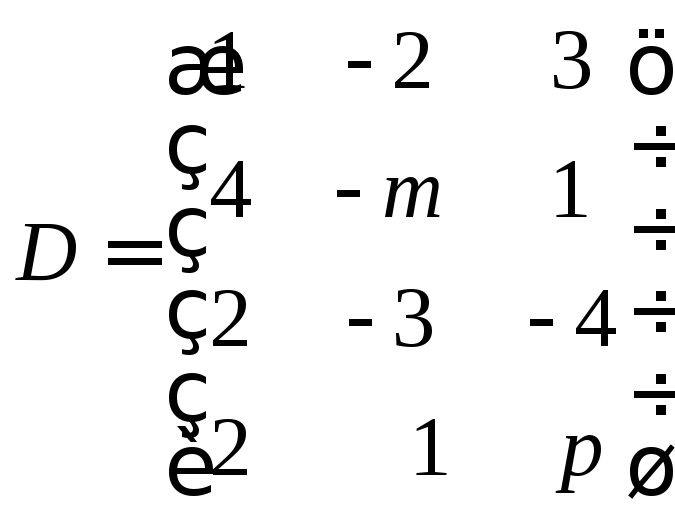 .
.
Вычислить:
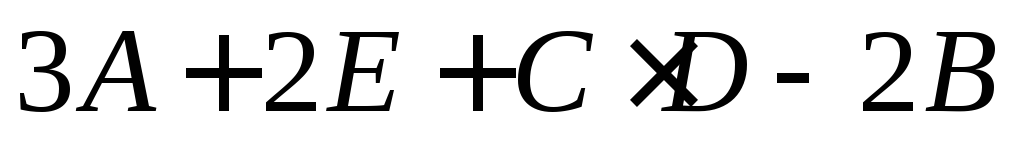 ,
где
,
где - единичная матрица;
- единичная матрица;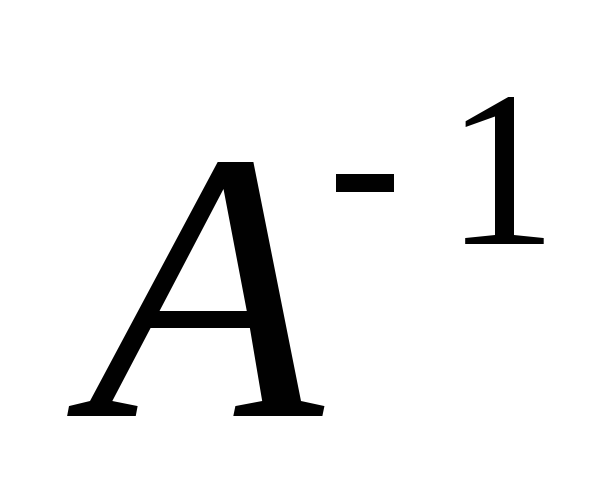 (вычисления проводить, сохраняя три
знака после запятой).
(вычисления проводить, сохраняя три
знака после запятой).
3. Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы:
а)
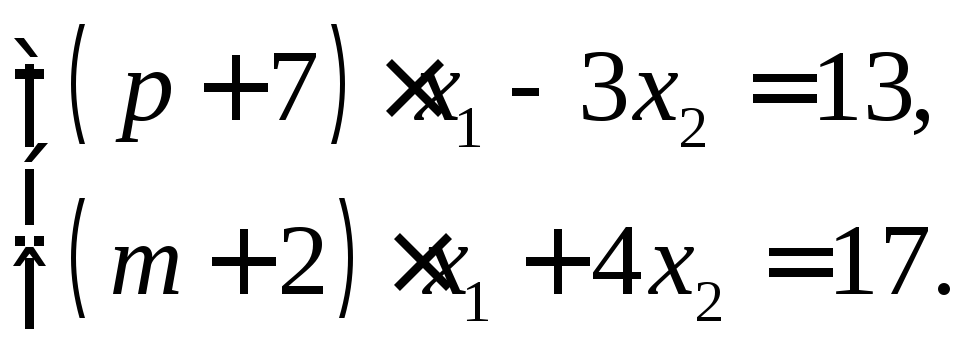 б)
б)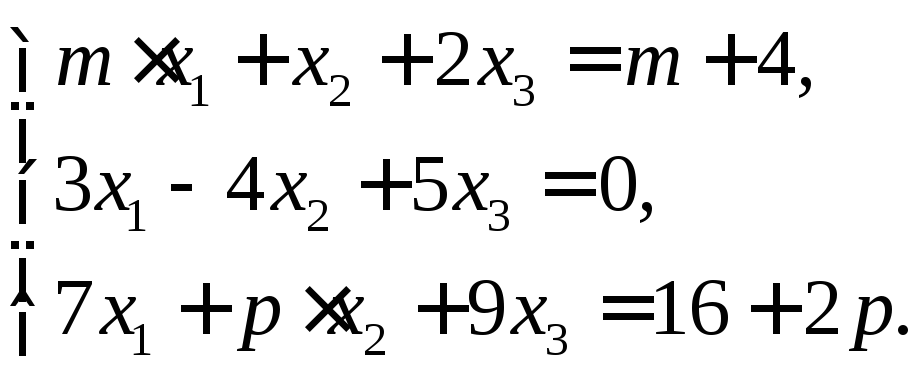
4.Исследовать и решить системы уравнений:
а)
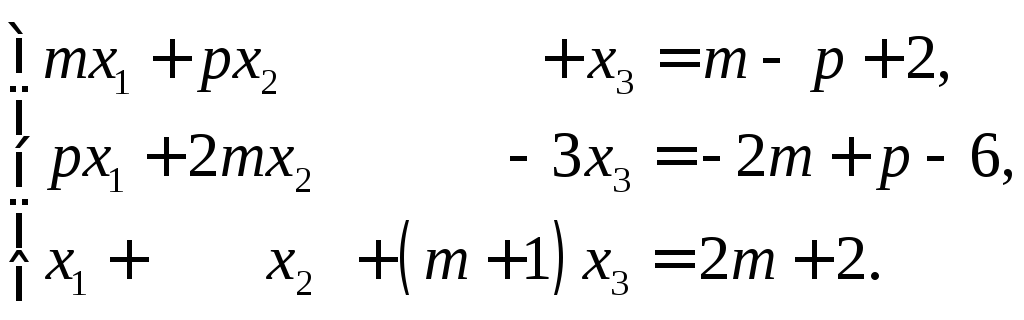
б)
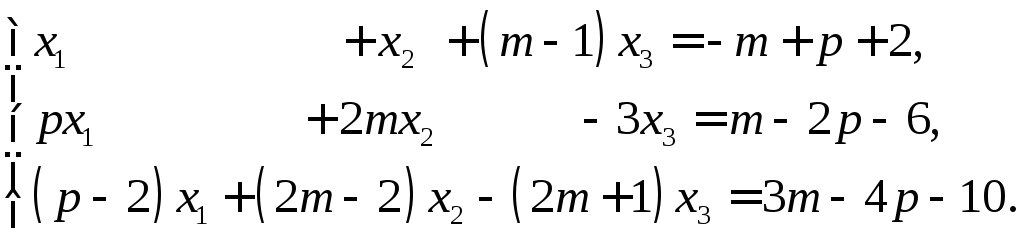
в)
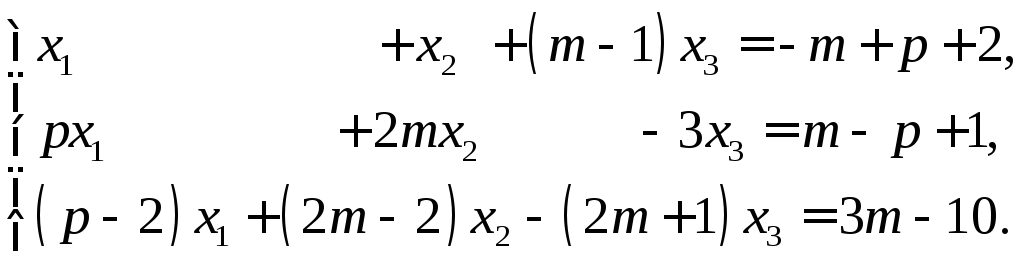
Приложение 1 Действия с матрицами на компьютере в excel.
Рассмотрим применение табличного процессора EXCELдля работы с матрицами.
Табличный процессор EXCELработает с числовыми матрицами и может осуществлять следующие операции:
сложение (вычитание) матриц, умножение матриц на число,
преобразования матрицы с целью получения нулей,
вычисление определителя матрицы,
транспонирование матрицы,
нахождение обратной матрицы.
Сложение матриц, умножение матриц на число, преобразование матрицы осуществляются с помощью строки формул. Для нахождения определителя транспонированной матрицы, обратной матрицы, а также умножение матриц следует пользоваться соответствующими встроенными функциями: МОПРЕД; ТРАСП; МОБР; МУМНОЖ., К сожалению, нет встроенной функции для определения ранга матрицы. Ранг придется находить переходом к эквивалентной матрице. Такой переход полезен и для исследования линейных систем.
Сложение матриц.
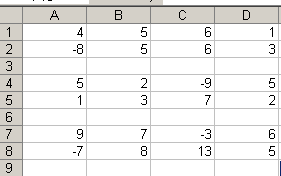
В ячейки
![]() введена матрица
введена матрица![]() .
.
В ячейки
![]() введена матрица
введена матрица![]() .
.
В ячейку
![]() введена формула
введена формула![]() и скопирована в диапазон
и скопирована в диапазон![]() .
.
Умножение матрицы на число.
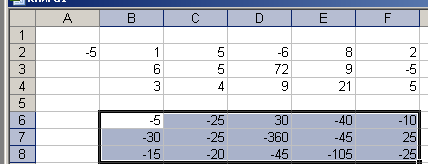
В ячейки
![]() введена матрица
введена матрица![]() ,
,
В ячейку
![]() введено число
введено число![]() .
.
В ячейку
![]() введена формула
введена формула![]() и скопирована в диапазон
и скопирована в диапазон![]() .
.
Вычисление определителя, транспонирование, нахождение обратной матрицы.
Перечисленные операции проводятся с помощью соответствующих встроенных функций.
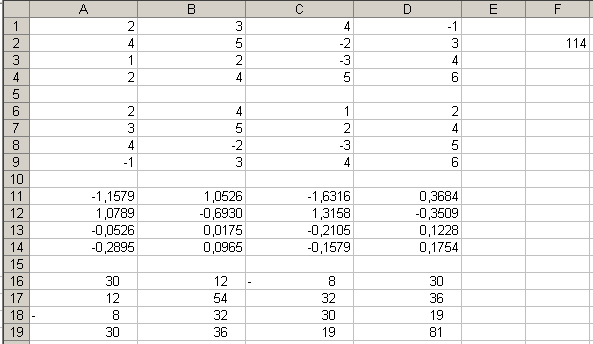
В ячейки
![]() введена матрица
введена матрица![]() ,
в ячейки
,
в ячейки![]() - матрица
- матрица![]() .
.
В ячейку
![]() введем формулу
введем формулу![]() =МОПРЕД,
заполним поле значений аргумента
=МОПРЕД,
заполним поле значений аргумента![]() ,
получаем значение определителя матрицы
,
получаем значение определителя матрицы![]() .
.
При выполнения операций транспонирования,
умножения матриц, нахождения обратной
матрицы необходимо предварительно
выделить диапазон ячеек для записи
результата. Результат получается
нажатием клавиш
![]() (ввод
массива).
(ввод
массива).
Пример.Вычислить обратную
матрицу для![]() .
.
Выделить диапазон ячеек
![]() для записи обратной матрицы.
для записи обратной матрицы.
Вызвать Мастер функций, выбрать имя
функции МОБР, ввести в поле значений
аргумента функций
![]() и нажать клавиши
и нажать клавиши![]() (ввод
массива).
(ввод
массива).
Пример. Умножить матрицы![]() и
и![]() .
Определим размерность результата6 4*4,
и выделим диапазон
.
Определим размерность результата6 4*4,
и выделим диапазон![]() для записи умножения двух функций.
для записи умножения двух функций.
Вызвать Мастер функций, выбрать имя
функции МУМНОЖ, Ввести в поле значений
аргумента функций 1 первую матрицу для
умножения
![]() ,
в поле 2 – вторую матрицу
,
в поле 2 – вторую матрицу![]() и нажать клавиши
и нажать клавиши![]() (ввод
массива). В ячейках
(ввод
массива). В ячейках![]() - результат умножения
- результат умножения![]() .
.
Преобразование матрицы в эквивалентную матрицу проведем, последовательно получая нули в первом, втором и т.д. столбцах ниже диагональных элементов.
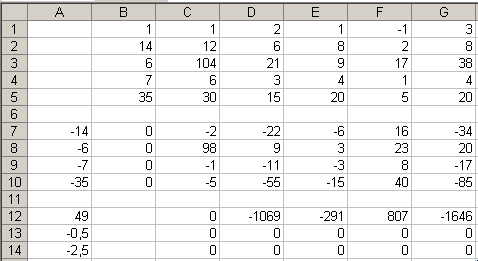
В ячейки
![]() введем заданную матрицу.
введем заданную матрицу.
Получим нули в первом столбце матрицы
![]() .
.
В ячейку
![]() введем формулу
введем формулу![]() и скопируем ее в ячейки
и скопируем ее в ячейки![]() .
.
В ячейку
![]() введем формулу
введем формулу![]() и скопируем ее в ячейки
и скопируем ее в ячейки![]() .
.
Аналогично получаем нули во втором столбце.
В ячейку
![]() введем формулу
введем формулу![]() и скопируем ее в ячейку
и скопируем ее в ячейку![]() .
.
В ячейку
![]() введем формулу
введем формулу![]() и скопируем ее в ячейки
и скопируем ее в ячейки![]() .
.
Вычисления прекращаются, так как мы получили нижележащие строки нулевые. Эквивалентная матрица имеет вид (нулевые строки отброшены)
-
1
1
2
1
-1
3
0
-2
-22
-6
16
-34
0
0
-1069
-291
807
-1646
.
Следовательно, ранг матрицы равен трем.
Табличный процессор EXCELориентирован на работу с числами. Однако существуют специализированные пакеты, например,MATHCADMATHEMATICAв которых возможны символьные операции, и работа с такими пакетами значительно помогает решению задач и проведению исследований.
1Элементами матрицы могут быть и другие математические объекты, при этом свойства, рассмотренные для числовых матриц, в основном сохраняются.
