G_МС

2

1 3

F₁ F₂

F

Рис. 3.1

В 1-м варианте загрузки ТК верхняя частота МС не меняется и равна F₂, и , аналогично (1.6) изменяется только верхняя частот МС согласно формуле

F_1i=F₂– 1,1N_iΔF_к, (3.1)

где N_i – количество загружаемых ТК, изменяющаяся от 0 до максимального количества ТКN.

Аналогично (1.10) и (1.13) относительная мощность дискретной составляющей определяется формулой

a_д1i = exp( - Δf²_эсi / F₂ F_1i) , (3.2)

где аналогично (1.4) и (1.5)

Δf²_эсi=f²_к0,05N_i. (3.3)

Во 2-м варианте не меняется нижняя F₁и верхняяF₂частоты МС при изменении способа загрузки. Меняется только спектральная плотность МС пропорционально количеству загружаемых телефонных каналов. В этом варианте

a_д2i=exp( -Δf²_эсi /F₂F₁). (3.4)

В 3-м варианте не меняется нижняя частота модулирующего сигнала F₁. Изменяется только верхняя частота модулирующего сигнала в зависимости от количества загружаемых телефонных каналов аналогично (1.6)

F_2i =F₁+ 1,1N_iΔF_тк. (3.5)

В этом варианте

a_д3i = exp( - Δf²_эсi / F_2i F₁). (3.4)

Результаты расчета мощности несущей без предыскажений МС (a1,a2,a3) и с предыскажениями МС, применяемыми на РРЛ, (aр1,aр2,aр3) приведены на рис. 3.2, выполненные с использованием Маткад-2001 с шагомN/20. Число после переменных а и ар соответствует варианту загрузки телефонными каналами. Приводимая на рис. граница порогаBporоценивать вид спектра ЧМ сигнала: большая (Δf²_эсi>>F₂F₁) или малая девиации частоты. Программа прилагается в электронном виде к лабораторной работе, но может быть выполнена вручную или на другом языке программирования.

Анализ кривых на рис. 3.2 позволяет сделать следующие выводы:

1. Введение предыскажений, применяемых на РРЛ, существенно увеличивает мощность несущей и поэтому не применим для ССС.

2. Наиболее эффективен 3-й вариант загрузки МС ТК, т.к. при изменении загрузки мощность несущей существенно не меняется. Только при приближении N_iк нулю мощность несущей возрастает. Поэтому этот вариант применялся для ССС.

3. Вытекает из п.2 : сигнал дисперсии (СД) или рассеяния мощности несущей целесообразно располагать ниже частоты спектра МС

Снижение мощности несущей актуальной при использовании цифровых ССС. С точки зрения подавления мощности несущей амплитудная модуляция не позволяет решить эту задачу, т.к. при ее использовании несущая существует всегда и существенна по величине также, как при использовании частотной модуляции. Для этих целей наиболее подходящими являются использование фазовой модуляции и квадратурной амплитудной модуляции.

Большие девиации частоты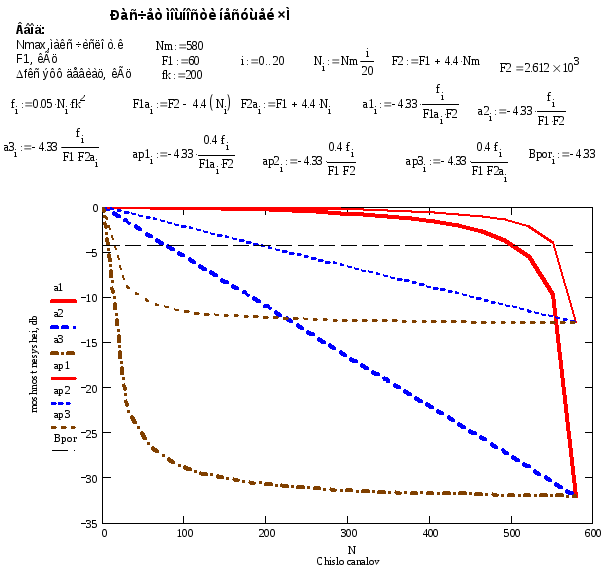

Рис. 3.2

О

той диаграммой подразумевается значения цифрового сигнала, описываемые формулой

u_c = U cos (ώ_ct + ψ), (3.5)

где ψ = 0^о, 180^о, в низкочастотной области при нулевом значении ώ_cи единичной значенииU, т.е.

u_c=cosψ. (3.6)

становимся на простейшем случае использования 2-х позиционной фазовой модуляции, диаграмма состояния сигналов которой приводится на рис. 3.3. Под вышеупомяну-

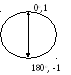
Рис. 3.3

Подавление мощности несущей происходит при одинаковой вероятности появления фаз цифрового сигнала 0^о,1 и 180^о, -1. Это условие выполняется автоматически при рандомизации цифрового сигнала, связанного со стандартным преобразованием исходного передаваемого цифрового сигнала путем его сложения по модулю 2 с синхронной псевдослучайной импульсной последовательностью. Последняя обладает этим свойством и позволяет практически устранить эту несущую на интервале периода псевдослучайно импульсной последовательности. Аналогичная ситуация возникает при многопозиционных фазовой и квадратурноамплитудной типах модуляции. Однако на ограниченных интервале времени несущая может появиться, как несущая мгновенного спектра. Но высказанное предположение требует проведения дополнительных исследований.