
ЦОС_Lek_1
.doc
Лекция 1. Введение в ЦОС
-
Дисциплина ЦОС.
-
Основные типы сигналов.
-
Дискретное и дискретное нормированное время.
-
Типовые дискретные сигналы.
-
Нормирование частоты.
-
Основная полоса частот.
-
Обобщенная схема ЦОС.
1.1. Дисциплина ЦОС
ЦОС — это ________________________________________________________
Кратко технологию ЦОС можно сформулировать так:
-
разработка метода ЦОС;
-
разработка алгоритма ЦОС;
-
компьютерное моделирование алгоритма ЦОС;
-
создание программного продукта (soft product);
-
реализация алгоритма в виде цифрового устройства (hard product).
Для того чтобы овладеть этой технологией необходимо получить знания в следующих областях:
-
Фундаментальная теория ЦОС.
-
Средства компьютерного моделирования ЦОС.
-
Цифровая элементная база для реализации алгоритмов ЦОС (ЦСП, ПЛИС и т.п.)
В рамках данного курса изучаются базовые методы и алгоритмы ЦОС, инвариантные относительно физической природы сигнала, и средства их компьютерного моделирования в MATLAB.
1.2. Основные типы сигналов
Сигнал — это ____________________________________________________________
Аналоговый сигнал — это сигнал, ___________________________________
Описывается непрерывной или
кусочно-непрерывной функцией
![]() (рис. 1.1, а).
(рис. 1.1, а).
Дискретный сигнал — это сигнал, _________________________________________
Описывается последовательностью
чисел бесконечной разрядности
![]() ,
которую называют коротко последовательностью
(рис. 1.1, б).
,
которую называют коротко последовательностью
(рис. 1.1, б).
Значения
![]() называют отсчетами.
называют отсчетами.
В теории ЦОС термины "дискретный сигнал" и "последовательность" употребляют в тождественном смысле!
Цифровой сигнал — это сигнал, ____________________________________
Описывается последовательностью
чисел конечной разрядности —
квантованной последовательностью
![]() (рис. 1.1, в).
(рис. 1.1, в).

Рис. 1.1. Типы сигналов: а) аналоговый; б) дискретный (последовательность); в) цифровой (квантованная последовательность)
1.3. Дискретное и дискретное нормированное время
Дискретным временем называют
значения
![]() ,
где
,
где
![]() —
_____________
—
_____________
Дискретным нормированным
временем называют значения
![]() :
:
![]() .
(1.1)
.
(1.1)
В этом случае формально
![]() ,
,
![]() имеет смысл ____________________, а значения
отсчетов остаются неизменными:
имеет смысл ____________________, а значения
отсчетов остаются неизменными:
![]() .
.
1.4. Типовые дискретные сигналы
Следующие типовые дискретные сигналы будут использоваться в дальнейшем.
-
Цифровой единичный импульс:
![]() (1.2)
(1.2)
Это аналог δ-импульса, но в отличие него, — ________________

Рис. 1.2. Цифровой единичный импульс: а) не задержанный; б) задержанный
Задержанный цифровой единичный
импульс имеет вид (задержка
![]() ):
):
![]() (1.3)
(1.3)
Подобно δ-импульсу, цифровой единичный импульс обладает фильтрующим свойством: ___________________________________________________________
![]() .
(1.4)
.
(1.4)
Пример 1.1
Определить, чему
равна правая часть (1.4) при
![]() .
.
-
Цифровой единичный скачок:
![]()

Рис. 1.3. Цифровой единичный скачок: а) не задержанный; б) задержанный
-
Дискретная экспонента:
 (1.5)
(1.5)

Рис. 1.4. Дискретная экспонента: а) знакопостоянная (а); знакопеременная (б)
-
Дискретный гармонический сигнал:
Соответствует аналоговому сигналу
![]()
при переходе
![]() (рис. 1.5):
(рис. 1.5):
![]() (1.6)
(1.6)

Рис. 1.5. Аналоговый (огибающая) и дискретный гармонические сигналы
-
Дискретный комплексный гармонический сигнал:
Соответствует аналоговому сигналу
![]()
при переходе
![]() :
:
![]() .
(1.7)
.
(1.7)
Физически — это два сигнала:
![]() .
.
1.5. Нормирование частоты
Пример 1.2
Записать две дискретные гармоники (1.6) при следующих исходных данных:
-
 ;
;  ;
;
 :
:
![]()
-
 ;
;  ;
;
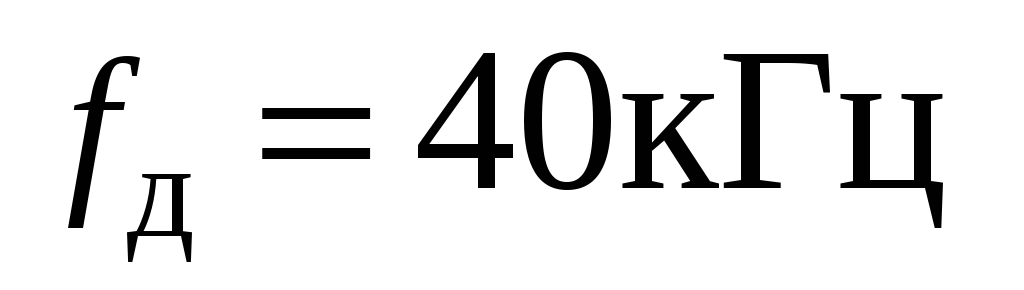 .
.
![]()
Получены __________________ гармонические сигналы, т.к. в них имеем одинаковое отношение ______________
По этой причине в ЦОС,
помимо абсолютных частот
![]() (Гц) и
(Гц) и
![]() (рад/с) используются нормированные
частоты:
(рад/с) используются нормированные
частоты:
![]() ;
;
![]() ,
,
откуда
![]() (рад). (1.8)
(рад). (1.8)
1.6. Основная полоса частот
Согласно теореме
Котельникова, точное восстановление
аналогового сигнала с финитным спектром,
ограниченным частотой
![]() ,
гарантируется при частоте
,
гарантируется при частоте
![]() :
:
![]() ________________
________________
Поэтому в ЦОС для
вещественных дискретных сигналов
вводится понятие основной
полосы частот
![]() :
:
![]() .
(1.9)
.
(1.9)
В шкале
![]() :
:
![]() ,
,
где
![]()
В шкале
![]() (1.8):
(1.8):
![]() .
(1.10)
.
(1.10)
При известной
частоте
![]() значение
значение
![]() легко определить из пропорции:
легко определить из пропорции:
![]()
![]()
1.7. Обобщенная схема ЦОС
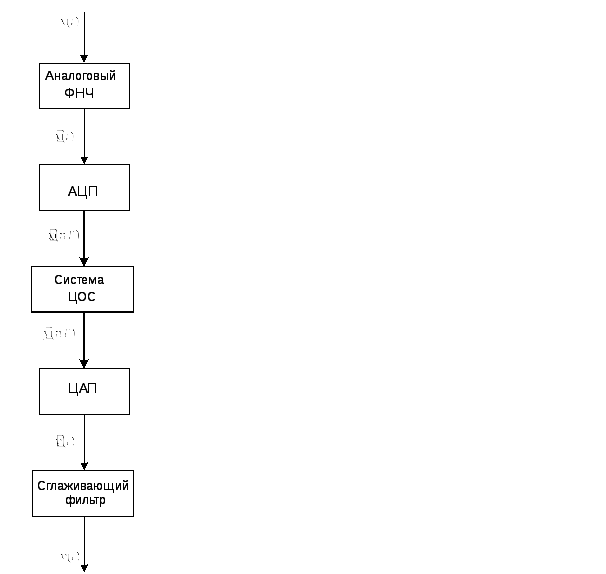
Рис. 1.6. Обобщенная схема ЦОС
ЦОС в реальном времени
означает, что алгоритм обработки сигнала
выполняется в темпе поступления отсчетов,
т. е. за период дискретизации
![]() .
.
