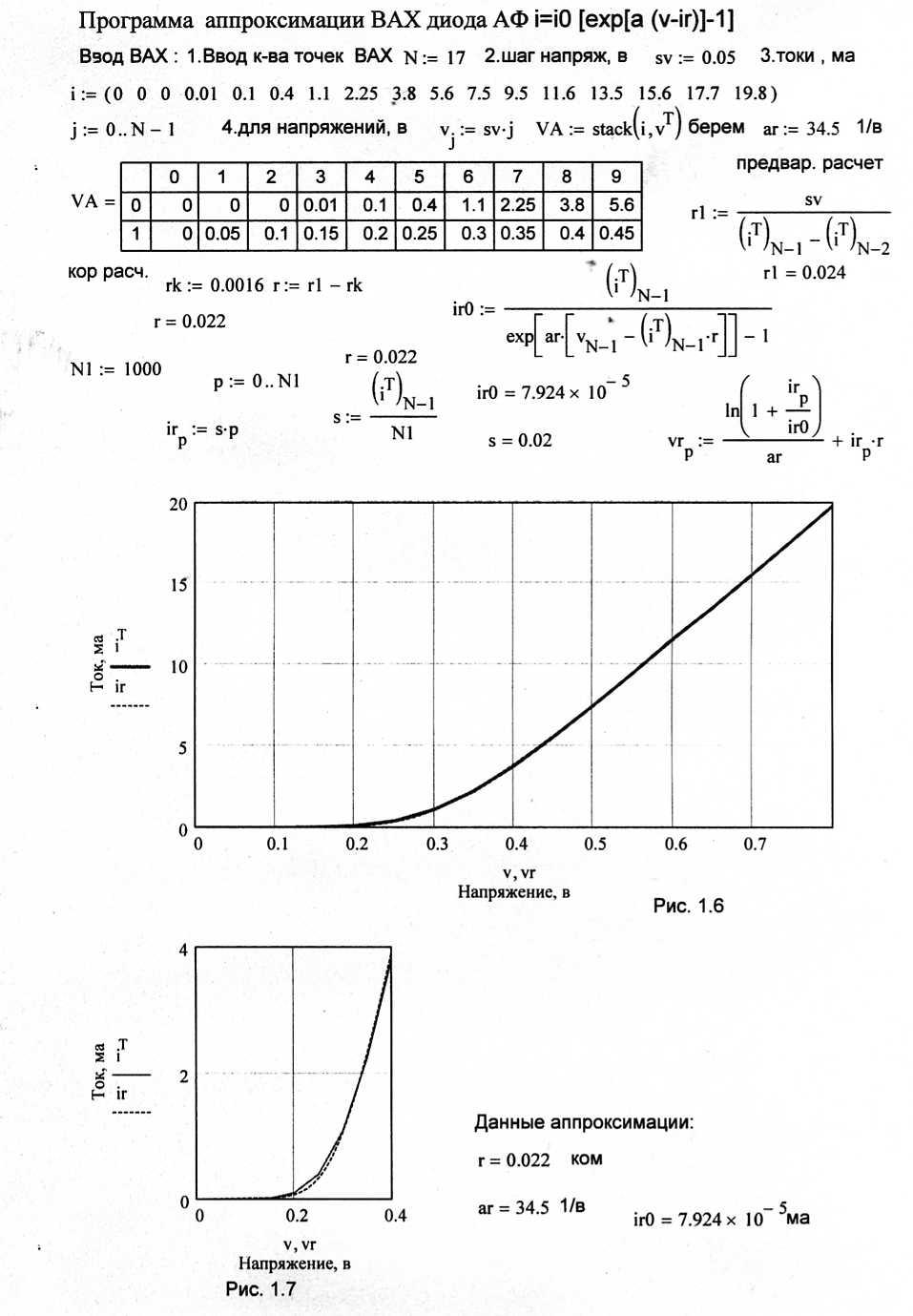
1.3.2. Экспоненциальная аф с сопротивлением

«Программа аппроксимации ВАХ диода АФ i = io{exp[a (v – ir)] – 1}» приведена на следующей странице в Пр.1.2. В отличие от АФ (1.19) здесь АП обозначены: (аr) = а, (ir0) = i₀, чтобы их отличать от близких по смыслу от АП других АФ. Описание ввода данных и вводимые данные аналогичны и приводятся в разделе 1.2.1. Так же как и там здесь вначале выбирается АП (аr) = 34,5 1/В по минимуму расхождения между данными тока i^T, заданными скопированной однострочной таблицы i.

Пр. 1.2

Далее рассчитывается АП r1 вначале как приближенное значение r, определяемая отношением разности приращений ВАХ диода по напряжению sv=0,05В к разности токов диода для максимального значения при N-1 и предшествующего N-2. Полученное решение является приближенным и не учитывает влияние изменения напряжения на р-n переходе диода. Для этого предлагается ввести коррекцию rk < 0.1 r1, вычитая его из r1: r = r1 – rk.

Полученные два АП позволяют рассчитать третий АП (i0r) по совпадению ВАХ и АФ для точки N-1. Полученная АФ рассчитывается по (1.20) для 10000 точек с шагом 0.002 мА до максимального значения 19.8 мА, приведенного в программе. Кривые ВАХ i^T приведены на рис. 1.6 для больших токов и на рис. 1.7 для малых токов, как функции напряжений v, кривые АФ напряжений (vr), как функции токов (ir). После нескольких коррекций двух АП получается практическое совпадение кривых ВАХ и АФ. При этом АП (аr) влияет на сходимость кривых для малых токов диода, АП r на сходимость кривых при больших токах диода. В отличие от предыдущей АФ (1.21) изменений АП не требуется при изменениях интервала Ар, т.к. кривые практически сливаются, а разработка новой модернизированной программы расчета сходимости для обратных функций внесет усложнения самой программы.

Для расчета АТКЧ необходимо располагать производными ВАХ диода р - порядка по напряжению. «Программа расчета производных по напряжению при использовании аппроксимации i = io{exp[a (v – ir)] -1}» приведена в Приложении 1.1 вплоть до производных 5 порядка. В эту программу вводятся АП: (аr), (ir0) и r, полученные в предыдущей программе.

Последовательно дифференцируя обратную функцию (1.20), получим:

(1.26)

(1.27)

где аналогично пояснениям к (1.25) здесь и далее служит для обозначений производных напряжений по току р - порядка. Производные вплоть до 3 порядка приведены в Приложении 1.1 и используются для вычисления производных тока по напряжению тоже до 3 порядка. Формулы связи функций производных с обратными функциями взяты из [8]. Графики расчета производных по этим формулам приводятся на рис. П1.1.1-П1.1.3. Там же приведены графики полученные с использованием приближенных методов дифференцирования (ПМД), например, для четвертой производной при использовании индекса р получим

(1.28)

В (1.28) переменной последняя буква р без цифры служит для информации о том, что расчет проводился с применением ПМД только 1 раз из расчетных значений, полученных расчетными методами по формулам. В приведенной в вышеупомянутой программе цифра 2 в производной вида информирует о том, что производная была получена двойным использования ПМД, т.е. вначале была получена , соответствующая (4.28) , а из нее также с помощью ПМД . Производные четвертого и пятого порядков производных АФ тока от напряжений приведены на рис. П1.1.4 и П1.1.5. Исследование тройного использования ПМД не выявило расхождения кривых на графиках между собой. В следующем разделе вышесказанной подтверждается пятикратным использованием этого метода в отличии от ПМ интегрирования (ПМИ), рассмотренного там же для инженерных расчетов при использовании Маткада.

Сравнивая производные по напряжению при использовании АФ ВАХ (1.21) и пояснения к ней в (1.25) с (1.19) и графиками производных в Приложении 1 можно сделать следующие выводы:

1. Максимальное значение производных происходит при напряжениях, соответствующих началу появления тока через диод.

2. Максимальные значения производных растут примерно в 3-4 раза медленнее, чем при использовании (1.19) для производных по напряжению первого и второго порядков. Только при переходе к производным третьего и более высоким порядкам скорость роста увеличивается примерно на порядок с увеличением порядка производной по напряжению на 1, как и при использовании экспоненциальной АФ.

3. Производные, начиная с третьего порядка, знакопеременны, что свидетельствуют о подобных изменениях АТКЧ согласно (1.15), пропаданию их при определенных напряжениях гетеродина или напряжениях смещения и появлению опять с дополнительным сдвигом по фазе на 180⁰.

4. Производные АФ практически не зависят от АП для рабочего режима при .

5. Численные расчеты графиков Приложения 1.1 показывают, что при уменьшении АП r в два раза с 22 Ом до 11 Ом при одной и той же амплитуде тока гетеродина приводят к увеличению максимумов и минимумов производных в два раза.

6. Аналогично при уменьшении АП (ar) c 34,5 В^-1 до 15 В^-1 привели к существенному уменьшению максимумов и минимумов производных, начиная со второй и далее приблизительно по закону: - порядок комбинационного преобразования согласно (1.12).

7. Колокольная форма второй производной при напряжениях близких к напряжению, соответствующему началу нарастания тока через диод, можно использовать для поиска других АФ ВАХ диодов, биполярных транзисторов и полевых транзисторов.

8. Использование ПМД позволяет довести до инженерного метода расчета ранее недоступные АФ из-за громоздкости вычислительных процедур, возможности ошибок при вычислениях и затруднениях в проверках результатов. Здесь простота алгоритма позволяет решить проблему расчета сравнительно быстро и проконтролировать его другими методами.