Парная регрессия в Statistica

В пустые столбцы (последние два) необходимо вставить из основной таблицы теоретически рассчитанные по уравнению регрессии значения переменной YY, и значения переменной x. В результате получим таблицу, изображенную на рис. 2.24.

Закроем эту таблицу. В результате на диаграмме рассеяния появится новый график (рис. 2.25)

Щелкнув правой кнопкой мыши на какой-либо точке нового графика, и выбрав в выпадающем меню команду Свойства графика, можем отредактировать его вид (рис. 2.26): изменить тип, размер и цвет меток и линий, включить легенду и др.

Рис. 2.26. Окно редактирования вида графика

9.Постройте доверительную область для линии регрессии.

Для построения доверительной области линии регрессии введем в исходную таблицу дополнительно три столбца: для вычисления ошибки регрессии Sp, нижней доверительной границы y_low и верхней доверительной границы y_hight.

На рис. 2.27 приводится пример определения переменной Sp – ошибки среднего предсказанного значения:

44

Среднее значение переменной x и ее дисперсия взяты из таблицы описательных статистик (п.2). Стандартная ошибка регрессии выдается в таблице итогов регрессии Se=2,29497.

Рис. 2.27. Расчет ошибки для линии регрессии

Нижняя и верхняя границы среднего предсказанного значения (доверительные границы регрессии) опре-

Рис. 2.28. Вид таблицы с добавленными столбцами – доверительными границами линии регрессии

Для построения доверительных границ на диаграмме рассеяния, воспользуемся тем же алгоритмом, что и для добавления линии регрессии (рис.2.22 -2.26). Результат показан на рис. 2.29.

45

Рис. 2.29. Диаграмма рассеяния с линией регрессии

иее доверительным интервалом

10.Оцените качество построенной модели через среднюю относительную ошибку аппроксимации. Определите среднеквадратическую ошибку модели.

Для расчета относительной ошибки аппроксимации и среднеквадратической ошибки добавим новые переменные в исходную таблицу – МАРЕ (рис. 2.30) и MSE. Они вычисляются по формулам:

Результаты определения новой переменной МАРЕ, приводятся на рис. 2.28 (последний столбец).

Рис. 2.30. Определение переменной для расчета относительной ошибки аппроксимации

46

Аналогично определим и переменную MSE. Обратим внимание, что в формулах мы вводим только выражение стоящее под знаком суммы.

Остается вычислить среднее значение по столбцам. Для этого щелкнем правой кнопкой мыши на названиях столбцов и в выпадающем меню выполним последовательно команды Блоковые статистики→По столбцу → Среднее (рис.2.31).

Рис. 2.31. Меню расчета блоковых статистик

В результате появится дополнительная строка, в которой вычислены среднее значение по столбцам, т.е. искомые характеристики – средняя относительная ошибка аппроксимации MAPE и средняя квадратическая ошибка MSE. Получили МАРЕ = 2,99% (рис. 2.32). Эта величина меньше 10%, следовательно, точность модели высокая. MSE=3,7621. Эти характеристики будут использоваться для сравнения с нелинейной моделью регрессии. Чем меньше эти обе ошибки, тем точнее считается построенная модель.

Рис. 2.32. Таблица данных с вычисленными ошибками MAPE и MSE

11. Определите средний коэффициент эластичности.

Средний коэффициент эластичности переменной y по переменной x можно вычислить, зная коэффициент b1 и средние значения переменных x и y:

Cредний коэффициент эластичности 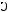показывает, что при увеличении среднемесячной заработной платы (x) на 1% доля расходов на питание (y) уменьшится (знак «минус») на 0,59%.

12. Дайте экономическую интерпретацию построенной модели.

47

Уравнение регрессии является достаточно точным. Относительная ошибка аппроксимации составляет всего 3% (МАРЕ=2, 99%). Коэффициент b1= -5,51987 показывает, что при увеличении x – среднемесячной заработной платы на одну тысячу доля расходов на питание - переменная y – в среднем уменьшается на 5,5%. Построенное уравнение регрессии на 89% объясняет поведение зависимой переменной y (показатель R2=0,8876). Средний ко-

эффициент эластичности говорит о том, что увеличение средней заработной платы на 1% приведет к уменьшению доли расходов на питание на 0,59%. В целом модель адекватна исходным данным и может применяться для прогноза.

************************ Нелинейная модель парной регрессии ************************

13. Рассчитайте параметры одной из функций регрессии в соответствии с выдвинутой гипотезой (п.2).

Нами было выдвинуто предположение, о том, что нелинейная регрессия может иметь форму степенной, экспоненциальной или гиперболической функции. Рассмотрим для примера степенную модель:

Эту модель можно линеаризовать, прологарифмировав обе части равенства:

.

вид:

Организуем новую таблицу для расчетов параметров степенной модели. Для этого выполним команду Файл →Создать или щелкнем на кнопке, изображающей чистый бланк на панели инструментов Стандартная (первая кнопка).

В появившемся диалоговом окне укажем, что создаем таблицу, содержащую 11 переменных и 7 наблюдений. Скопируем из имеющейся таблицы данных значения переменных x и y, рассчитаем в следующих двух столбцах преобразованные переменные

. В программе Statistica натуральный логарифм вычисляется с помощью встроенной функции Log( ).

Рис. 2.33 Таблица данных для построения нелинейной модели регрессии

В результате получим таблицу, изображенную на рис. 2.33. Если таблица создалась в отдельно расположенном окне, то для удобства работы ее лучше поместить в нашу рабочую книгу. Для этого щелкнем в окне таблицы на ее названии (сделаем окно с таблицей активным) и на панели инструментов Стандартная нажмем кнопку Добавить в рабочую книгу. В раскрывшемся списке выберем имя нашей рабочей книги.

6. Определите параметры уравнения нелинейной регрессии и дайте интерпретацию коэффициентов регрессии.

Определим параметры b0 и b1 линеаризованного уравнения регрессии, используя модуль Множественная регрессия. Для этого выполним команду Анализ → Множественная регрессия. Нажав на кнопку Переменные в стартовом окне модуля, попадем в окно выбора переменных для анализа (рис. 2.14), в котором в качестве зависимой переменной укажем W, а в качестве независимой – Z. Подтвердим ввод переменных в этом окне, и, вернувшись в стартовое окно модуля Множественная регрессия, подтвердим определение модели.

Откроется окно результатов множественной регрессии, подобное изображенному на рис. 2.15.

При нажатии кнопки Итоговая таблица регрессии Ststistica выдает две таблицы с результатами анализа: Итоговые статистики - таблицу, в которой отражены основные показатели из информационного окна; таблицу Итоги регрессии для зависимой переменной: W - значения и характеристики коэффициентов регрессии (рис. 2.34).

48

Рис. 2.34. Итоги регрессии.

Запишем линеаризованное уравнение регрессии, подставив вычисленные коэффициенты:

Коэффициент детерминации R2=0,8876. Это означает, что почти 89% вариации результативного признака W объясняется вариацией признака Z.

Для записи степенной формы уравнения регрессии необходимо вернуться к исходным переменным и параметрам:

Уравнение регрессии примет вид:

Интерпретация коэффициента b1: в степенной модели данный коэффициент является средним коэффициентом эластичности. Он показывает, что при увеличении средней заработной платы на 1% доля расходов на питание уменьшится на 0,57% (вывод формул – см. ниже).

Введем в нашу таблицу дополнительные столбцы – для рассчитанного по уравнению регрессии значения W и значения переменной у. Назовем соответствующие переменные W_t и y_t.

Значения переменной W_t мы можем вычислить по формуле

Другой способ - скопировать из столбца Предск. значение таблицы Остатки и предсказанные. Для вывода этой таблицы необходимо выполнить следующее: в окне Результаты множественной регрессии перейти на вкладку Остатки/ предсказанные/ наблюдаемые значения, выбрать кнопку Анализ остатков, и в появив-

шемся одноименное окне нажать на кнопку Остатки и предсказанные. Обратите внимание, что последние четыре строки (итоговые статистики) предсказанных значений переменной W копировать не надо (рис. 2.35).

Рис. 2.35. Таблица Предсказанные значения и остатки для степенной модели

49

Значения переменной y_t вычисляются по формуле

Кроме этого для дальнейших расчетов нам понадобится определить ошибку степенной модели и сумму квадратов ошибок. Для этого добавим в нашу таблицу две новые переменные: E1 – для вычисления ошибки модели, и E12 – для вычисления квадрата ошибки.

Результат вставки значений W_t и расчета значений y_t, E1 и E12 представлены на рис. 2.36.

Рис. 2.36. Таблица данных с новыми переменными

7.С вероятностью 0,95 оцените статистическую значимость уравнения регрессии в целом и каждого параметра.

а) Проверим значимость уравнения регрессии в целом.

Проверяемая гипотеза: H0: R2=0; альтернативная гипотеза: H1: R2≠0 . Для линеаризованной модели

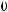
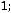
коэффициент детерминации статистически значим при уровне надежности 0,95%. Это следует из того, что рассчитанное по нашим данным значение F-статистики . Нулевая гипотеза отклоняется.

Здесь возникает проблема, описанная в Замечании п. 2.3 (Парная нелинейная регрессия): коэффициент детерминации вычислен для переменных , а не для исходных переменных y и x. Для степенной модели необходимо рассчитать индекс детерминации:

Для нахождения средней квадратической ошибки MSE по столбцу Е2 необходимо вычислить блоковую статистику – сумму (рис. 2.36) и поделить вычисленное значение на число наблюдений. В результате получим MSE=2,32355 Дисперсия переменной известна (см. Описательные статистики - п.2 задания, рис. 2.7) 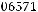. Тогда индекс детерминации равен

Оценка статистической значимости индекса детерминации осуществляется так же, как и оценка значимости коэффициента детерминации - с помощью F-критерия Фишера с заменой на :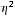

Для нашего примера n=7, p=1 (число факторов), тогда k1=1; k2=7-1-1=7-2=5. Вычисленное значение F- критерия больше 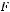. Значит гипотеза отклоняется. Уравнение в целом значимо.

50

б) Для проверки значимости коэффициентов уравнения регрессии используется t-статистика Стьюдента. Выборочные значения этой статистики для каждого коэффициента представлены в таблице (рис. 2.34) в столбце t(5):

Так как оба значения по модулю больше tкр=t(0,95; n-p-1)=t(0,95; 5)= 2,0128, то оба коэффициента признаются статистически значимыми (отличными от нуля).

8.Отобразите на поле корреляций теоретически рассчитанную линию регрессии.

Для построения поля корреляций выполним команду Графика→ Диаграммы рассеяния. Дальнейшие действия те же, что и в инструкции по выполнению заданий п.3 и п.8 линейной модели регрессии. В результате получим график, изображенный на рис.2.38 (средняя кривая).

9.Постройте доверительную область для линии регрессии.

Для построения доверительной области линии регрессии так же, как и в случае линейной модели, введем в

таблицу три новые переменные: для вычисления ошибки регрессии Sp, нижней доверительной границы y_low и верхней доверительной границы y_hight. Обратите внимание, что стандартная ошибка модели вычисляется по формуле:

Дальнейший алгоритм – такой же, как и для линейной модели регрессии. Расчеты этих переменных приведены на рис. 2.37. Кривая линии регрессии и границы доверительной области изображены на рис. 2.38.

Рис. 2.37. Таблица с вычислением доверительных границ для линии регрессии.

10.Оцените качество построенной модели через среднюю относительную ошибку аппроксимации. Определите среднеквадратическую ошибку модели.

Для вычисления средней ошибки аппроксимации введем в таблицу дополнительный столбец, назовем его MAPE1. Переменную определим так же, как и в случае линейной модели. Вычислив блоковую статистику – среднее по столбцу, получим значение искомой характеристики MAPE1=2,021( рис. 2.33).

Средняя квадратическая ошибка вычислена уже в задании п.7 для степенной модели: MSE=2,32297

11. Определите средний коэффициент эластичности.

Коэффициент эластичности (вообще, а не средний) вычисляется по формуле:

Он же и будет средним коэффициентом эластичности.

51

Рис. 2.38. Диаграмма рассеяния с добавленной линией регрессии

идоверительными границами

12.Дайте экономическую интерпретацию построенной модели.

Уравнение степенной линии регрессии имеет вид:

Параметр b1= - 0,57523 в степенной модели является коэффициентом эластичности, он показывает, что при увеличении средней заработной платы на 1% доля расходов на питание уменьшится на 0,57%.

Показатели качества построенного уравнения регрессии достаточно хорошие. Найденный нами индекс детерминации говорит о том, что 94% вариации результативного показателя y объясняется уравнением регрессии.

Средняя относительная ошибка MAPE1=2,021%, что меньше 10% - значит, точность модели – высокая. Средняя квадратическая ошибка MSE=2,32297 – также небольшая величина.

*************************** Конец исследования нелинейной модели регрессии ***********************

***************************************************************************************************

14 Выберете лучшую из моделей (п.5 или п.13), выбор обоснуйте.

Так как обе модели (и линейная, и степенная) являются достаточно точными, то возникают вопросы: какую из моделей лучше использовать, и так ли необходима нелинейная модель.

Выпишем основные характеристики построенных моделей:

Для ответа на второй вопрос проверим гипотезу о равенстве коэффициента детерминации линейной модели

52

Вычисленное с помощью вероятностного калькулятора критическое значение tкр=t(0,95; n)=t(0,95; 7)= 2,36468 больше . Значит, гипотеза принимается. По качеству модели практически не отличаются. Следовательно, не имеет смысла усложнять модель и можно остановить свой выбор на линейной модели регрессии.

15С вероятностью 0,95 постройте доверительный интервал ожидаемого значения результативного признака в предположении, что значение признака-фактора увеличится на 5% относительно своего среднего уровня.

Определим значение переменной xp, для которого необходимо предсказать по линейной модели значение зависимой переменной

Вернемся в стартовое окно модуля Множественная регрессия, выберем для анализа зависимую переменную y и независимую переменную x.

В окне результатов множественной регрессии перейдем на вкладку Остатки/ предсказанные/наблюдаемые значения. Установим уровень значимости 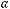, и нажмем кнопку Предсказать зависимую переменную (рис.

2.39).

Рис.2.39. Выбор параметров для прогноза по линейной модели

Впоявившемся диалоговом окне укажем значение зависимой переменной и нажмем кнопку ОК (рис. 2.40).

Врезультате появится таблица, в которой представлено предсказанное по линейному уравнению регрессии значение зависимой переменной , а также нижняя и верхняя границы доверительного 95%-ого

интервала (рис. 2.41).

53