1.7. Метод эквивалентного генератора (активного двухполюсника)

Метод и его применение. Метод эквивалентного генератора дает возможность часть сложной электрической цепи с источниками энергии и двумя выделенными выводами, т. е. активный двухполюсник (рис. 1.15, а), заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на выводах двухполюсника и внутреннее сопротивление — входному сопротивлению двухполюсника. Если в активный двухполюсник входят все элементы схемы, кроме одного выделенного сопротивления R, то можно найти- ток I в этом сопротивлении. Поэтому метод эквивалент- ного генератора рационально применять, если необходимо найти ток в одной ветви сложной электрической цепи, не рассчитывая токи в других ветвях.

Доказательство метода. В сложной электрической цепи (рис. 1.15, а), показанной в виде активного двухполюсника А с выделенным участком, сопротивление которого R, требуется найти ток I. Включим последовательно с сопротивлением R два источника ЭДС: Е' и Е" (риc. 1.15,б), с напряжениями, равными напряжению между выводами а и b активного двухполюсника при отключенном сопротивлении R, т. е. в режиме холостого хода. Е'==Е" = U = IR и направлены навстречу друг другу. Ток при этом не изменится.

В соответствии с принципом наложения схему рис1.15, б можно представить в виде двух вспомогательных схем, в одной из которых действует источник ЭДС E' и все источники внутри активного двухполюсника (рис. 1.15, в), а в другой— (рис. 1.15, г) действует только источник ЭДС Е", а источник Е' и все источники в активном двухполюснике не действуют, т. е. активный двухполюсник становится пассивным.

По принципу наложения ток I равен сумме частичных токов вспомогательных схем: I=I^’+I". Так как E' = E" = U_x, то во вспомогательной схеме рис. 1.15, в частичный ток I' равен нулю, что следует из закона Ома : I'== (U_x - E')/R. Следовательно, частичный ток I" (рис.1.15, г) равен искомому току I. По закону Ома

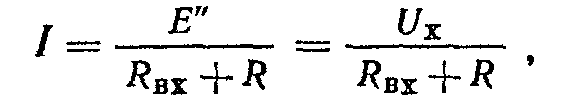(1.31)

где R_вх — внутреннее или входное сопротивление пассивного двухполюсника, т. е. сопротивление пассивного двухполюсника (рис. 1.15, г) относительно выводов а и b. Такой же ток будет и в схеме рис. 1.15,д, если E_э= U_x и R_э = R_вх. Ток I в сопротивлении исходной схемы (рис.1.15, а) и в схеме рис. 1.15, д один и тот же, т. е. активный двухполюсник можно заменить эквивалентным генератором.

Порядок расчета. Для расчета тока в сопротивлении R следует сначала отключить это сопротивление и определить напряжение U_x на его выводах. Далее нужно исключить все ЭДС в оставшейся части схемы (внутренние сопротивления источников остаются) и найти ее сопротивление относительно выводов отключенного сопротивления. Наконец, по (1.31) рассчитать искомый ток.

Пример 1.2. Найти токи в схеме методом контурных токов. Числовые значения сопротивлений в омах и э. д. с. в вольтах указаны на рисунке.

Рис. к примеру 1.2

Решение. Выберем направления всех контурных токов по часовой стрелке. Определяем: R₁₁ =

Записываем систему уравнений:

Определитель системы

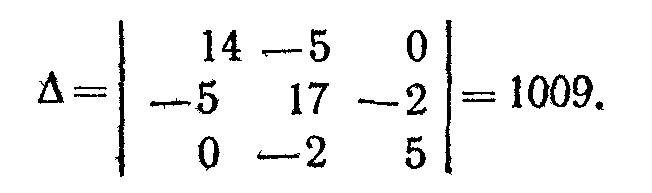
Подсчитаем контурные токи

Ток в ветви cm

Ток в ветви am

Пример 1.3. Методом эквивалентного генератора определить ток в диагонали аb мостовой схемы (рис.а), полагая R₁ = R₄ = 1 Ом; R₂ = 4 Ом; R₃ = R₅ = 2 Ом; Е₁ = 10 В.

Решение. Размыкаем ветвь аb (рис. б) и находим напряжение холостого хода:

Рис. к примеру 1.3.

Подсчитываем входное сопротивление всей схемы по отношению к зажимам ab при закороченном источнике э. д. с. (рис. в). Точки с и d схемы оказываются соединенными накоротко. Поэтому

Определим ток в ветви по формуле: