2.6. Индуктивный элемент в цепи синусоидального тока

Обмотки электрических машин и аппаратов, а также индуктивные катушки, используемые в различных устройствах радиоэлектроники, характеризуются параметром индуктивность L. Любая катушка наряду с L обладает также определенным активным сопротивлением г.

Рассмотрим катушку с индуктивностью L, активным сопротивлением которой можно пренебречь (г = 0), т. е. идеальную катушку (рис. 2.11, а). Пусть через нее проходит синусоидальный ток

(2.34)

Этот ток вызывает в катушке э. д. с. самоиндукции

(2.35)

Из формулы (2.35) следует, что э. д. с. самоиндукции отстает по фазе от тока на угол(рис. 2.11, б). Еслито =E_Lm =I_m ωL, а действующее значение э. д. с. самоиндукции

(2.36)

Напряжение на индуктивности

(2.37)

Сопоставляя уравнения (2.34) и (2.37), можно утверждать, что напря­жение на индуктивности изменяется, как и ток, по синусоидальному закону и что напряжение опережает ток на угол(рис. 2.11,6).

Еслитооткуда

(2.38)

Разделив правую и левую части (2.38) на получим закон Ома для цепи с индуктивностью

(2.39)

где— реактивное сопротивление индуктивности, или индуктивное сопротивление. Это сопротивление учитывает реакцию электрической цепи на изменение магнитного потока в индуктивности. Размерность

Видно, что индуктивное сопротивление пропорционально частоте.

Мгновенная мощность, выделяемая в индуктивном элементе,

(2.40)

откуда следует, что мгновенная мощность в цепи с индуктивностью изменяется, как и ток, синусоидально, причем с частотой в два раза большей, чем частота тока (рис. 2.11, б). Из рис. 2.11, б также видно, что за первую четверть периода, когда мощность положительна и ток возраста­ет от 0 до I_m, электрическая энергия поступает из электрической сети в индуктивный элемент, где она затрачивается на создание магнитного поля, причем ее затраты максимальны к концу первой четверти периода т. е. когда ток станет максимальным. Во вторую четверть периода ток убывает отI_m до нуля, напряжение и мощность отрицательны, а энергия магнитного поля, накопленная в индуктивном элементе, полностью выделяется в электрическую сеть. Во втором полупериоде картина повторяется. Следовательно, среднее значение мощности (активная мощность) цепи с идеальной катушкой за период равна нулю:

Итак, в цепи с индуктивным элементом непрерывно происходит обмен энергией между сетью (источником) и магнитным полем индуктивного элемента. Этот процесс протекает без потерь энергии на нагревание проводников электрической цепи, т. е. в цепи идет незатухающий коле­бательный процесс обмена энергией. Амплитуду колебания мощности в цепи с идеальной катушкой принято называть реактивной индуктив­ной мощностью:

Согласно (2.34) и (2.37), комплексные амплитуды тока и напряжения

Действующие комплексы тока и напряжения

(2.41)

На рис. 2.11, в представлено векторное изображение комплексных ве­личиндля ψ_i = 0. Из уравнения (2.41) получаем закон Ома в комплексной форме для цепи с индуктивным элементом:

(2.42)

где jX_L = jωL — комплекс индуктивного сопротивления.

Пример 2.1. Дано комплексное действующее значение тока I = - 4 –j3. Найти параметры синусоидальной функции времени — мгновенного значения тока, соответствующего заданному комплексному числу.

Решение. Действующее значение тока

амплитуда тока

начальная фаза тока

Искомое мгновенное значение тока

Угловая частота ω предполагается известной.

Пример 2.2. Заданы параметры синусоидального тока: амплитуда I = 56,5 А, начальная фаза ψ_i = —30°, угловая частота ω = 314 рад/с. Требуется записать мгновенное значение тока, рассчитать его комплекс­ное действующее значение в трех формах.

Решение:

Пример 2.3. Задано комплексное напряжение U = - 400+j300; ча­стота f = 50 Гц. Требуется найти, мгновенное значение напряжения u.

Решениe. Комплексное напряжение U из алгебраической формы

переведем в показательную

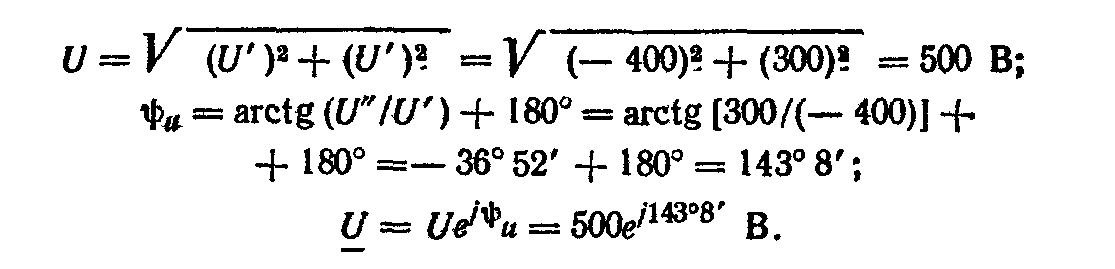
По известному действующему значению напряжения определим его амплитуду

Пример 2.4. В схеме рис. а) заданы э. д. с. е = 141 sin ωt в и параметры схемы: R₁ = 3 Oм; R₂= 2 Oм; L = 0,00955 Гн. Угловая частота  = 314 с ^-1. Определить ток и напряжение на элементах цепи.

Рисунок к примеру 2.4.

Решение. Запишем уравнение для мгновенных значений

Перейдем от него к уравнению в комплексах

где

Комплекс действующего значения э. д. с.

Находим

Напряжения на сопротивлении R₁

на сопротивлении R₂

на индуктивности

Рисунок к примеру 2.4.

Векторная диаграмма изображена на рис. б). Вектор E направлен по оси +1. Ток отстает от него на 31°.