11. . Свойство взаимности и принцип компенсации

Для схемы рис. 1.21, а ток в ветви с сопротивлением r_m равен

Исключим источник э. д. с. E_k из контура k и включим его в контур m (рис. 1.21,6) E_m = E_k согласно с положительным направлением тока I_m. Тогда методом контурных токов можно определить ток I_k в контуре k с сопротивлением r_k:

:

Так какиз-за симметрии определителя системы ∆ относительно главной диагонали, то ток I_m в схеме рис. 1.21,а окажется равным току I'_k в схеме рис. 1.21,6, что возможно при условии равенства взаимных проводимостей:

Следовательно, если э. д. с., включенная в один из контуров схемы, вызывает в другом контуре ток, то эта же э. д. с., перенесенная в этот, другой, контур, вызовет в первом контуре такой же ток.

Следует отметить, что такое свойство, называемое свойством взаимности, справедливо также для напряжений, что можно показать с помощью законов Кирхгофа. Свойство взаимности используют при расчете цепей, когда перенос источника питания из одной ветви в другую ведет к упрощению схемы.

Сущность принципа компенсации заключается в возможности заменять любое сопротивление ветви электрической цепи источником э. д. с., причем ток в цепи не изменяется, если сопротивление данной ветви заменять э. д. с., равной напряжению на зажимах ветви и направленной навстречу току в этой ветви.

Рассмотрим электрическую цепь, представляющую собой активный двухполюсник с подключенной к его зажимам ветвью с сопротивлением r, через которую протекает ток I (рис. 1.22, а). Если в эту ветвь помимо сопротивления г включить две э. д. с., направленных противоположно друг другу и численно равных напряжению на сопротивлении г (Е = Ir) (рис. 1.22,6), то ток в ветви ab не изменится. Однако в этом случае разность потенциалов между точками с и b будет равна нулю, так как ф_b = φ_с + Е - Iг = φ_c. Следовательно, точки b и c имеют одинаковый потенциал и их можно соединить между собой накоротко.

Это означает, что если в ветви аb вместо сопротивления r включена э. д. с. Е, то ток в ней не изменяется. Таким образом, любое сопротивление в электрической цепи можно заменить источником э. д. с., направленной навстречу току и равной напряжению на данном сопротивлении.

Пример 1.4. Найти токи в ветвях схемы и сделать проверку по второму закону Кирхгофа. Дано: E ′₄₁= 10 В, Е"₁₄ = 6 В,

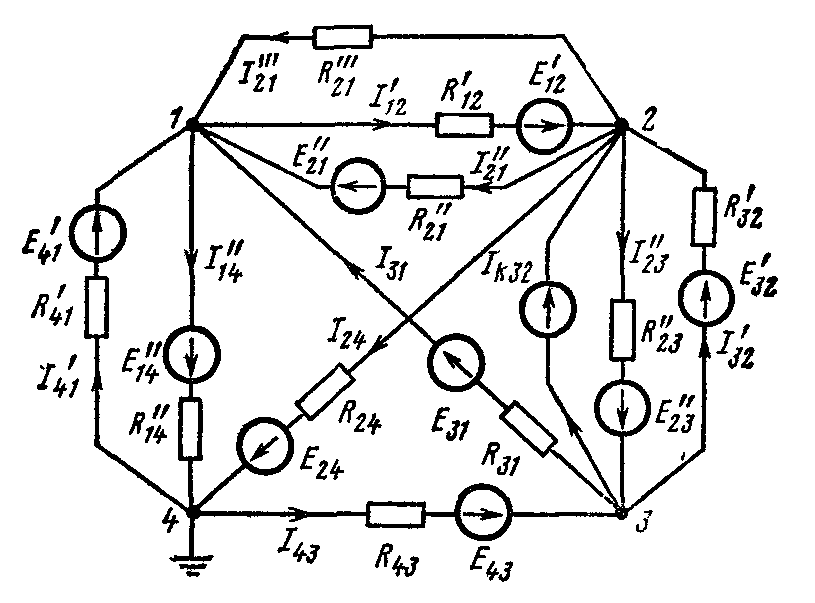
Рис. к примеру 1.4

Источник тока, включенный между узлами 3 и 2, дает ток I_k32 = 1,5 А.

Решение. Записываем систему уравнений:

Подсчитываем проводимости:

При подсчете G₂₂, G₃₃ и G₂₃ учтено, что проводимость ветви с источником тока равна нулю (сопротивление источника тока равно бесконечности).

Узловые токи:

Система уравнений:

2,4^.φ₁ – 0,4^.φ₂ – 0,5^.φ₃ = 15;

- 0,4^.φ₁ + 1,4^.φ₂ – 0,75^.φ₃ = - 1,5;

- 0,5^.φ₁ – 0,75^.φ₂ + 1,75^.φ₃ = - 5

имеет решение: φ₁ = 6 В; φ₂ = 0,06 В; φ₃ = -1,07 В.

Заключительный этап расчета состоит в подсчете токов по закону Ома. Перед определением токов в ветвях схемы следует эти токи обоз­начить и выбрать для них положительные направления:

Сделаем проверку решения по второму закону Кирхгофа для периферийного контура.

Алгебраическая сумма падений напряжений

^В.

Алгебраическая сумма э. д. с. В.

Пример 1.5. Найти токи в заданной схеме методом двух узлов и сделать проверку, составив баланс мощности, если

^.

Рис. к примеру 1.5

Решение:

В схеме потребляется мощность

I₁² R₁ + I₂² R₂ + I₃² R₃ + I₄² R₄ =

= 57,3 ^{2 .}2 + 1,35 ^{2 .} 4 + 55,4 ^{2 .}1 + 0,54 ^{2 .}10 = 9647 Вт.

Источники э. д. с. доставляют мощность

E₁I₁ – E₃I₃ = 120^.57,3 + 50^.55,4 = 9647 Вт