
- •Курс лекций по математике
- •§ 2. Способы задания множеств
- •§ 3. Отношения между множествами. Графическая иллюстрация множеств
- •§ 4. Операции над множествами
- •§ 5. Законы операций над множествами
- •Контрольные вопросы
- •§ 6. Число элементов объединения двух и трех конечных множеств
- •§ 7. Понятие разбиения множества на классы
- •Контрольные вопросы
- •Глава 2. Математические предложения § 1. Высказывания и операции над ними. Равносильные высказывания
- •§ 2. Законы алгебры высказываний
- •Контрольные вопросы
- •§ 3. Предикаты и операции над ними
- •Контрольные вопросы
- •§ 4. Высказывания с кванторами и их отрицания
- •Контрольные вопросы
- •§ 5. Отношение следование и равносильности между предложениями. Необходимое и достаточное условие
- •Контрольные вопросы
- •§ 6. Строение и виды теорем
- •Контрольные вопросы
- •Глава 3. Математические понятия § 1. Объем и содержание понятия. Отношения между понятиями
- •§ 2. Определение понятия. Требования к определению понятия
- •Контрольные вопросы
- •Глава 4. Математические доказательства § 1. Умозаключения и их виды
- •§ 2. Схемы дедуктивных умозаключений
- •§ 3. Проверка правильности умозаключений
- •§ 4. Способы математического доказательства
- •Контрольные вопросы
- •Глава 5. Соответствия §1. Упорядоченная пара. Декартово произведение двух множеств
- •§ 2. Соответствие между элементами множеств. Способы задания соответствий
- •§ 3. Взаимно однозначное соответствие
- •§ 4. Равномощные множества. Счетные и несчетные множества
- •Контрольные вопросы
- •§ 5. Определение числовой функции. Способы задания функций. Свойства функций
- •§ 6. Виды функций
- •§ 7. Обратная функция
- •Контрольные вопросы
- •Глава 6. Отношения на множестве § 1. Понятие отношения. Способы задания отношений
- •§ 2. Свойства отношений
- •§ 3. Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы
- •§ 4. Отношение порядка. Упорядоченные множества
- •Контрольные вопросы
- •Глава 7. Выражения. Уравнения. Неравенства § 1. Числовое выражение и его значение
- •§ 2. Числовые равенства и их свойства
- •§ 3. Числовые неравенства и их свойства
- •§ 4. Выражение с переменной, его область определения. Тождество.
- •§ 5. Уравнения с одной переменной. Равносильные уравнения
- •Глава 1. Элементы теории множеств 2
§ 6. Виды функций
Постоянная функция.
Определение. Постоянной называется функция, заданная формулойу=b, гдеb- некоторое число.
у=b
 у
у
Графиком является прямая, параллельная ости абсцисс и проходящая через точку с координатами (0; b).

 х
х
Прямая пропорциональность.
Определение. Прямой пропорциональностью называется функция,
заданная формулой у=k х, гдеk 0. Числоk называют коэффициентом
пропорциональности.
Свойства функции у=k х
Область определения – множество всех действительных чисел.
Множество значений – множество всех действительных чисел.
Функция нечетная, т.к. f(–х) =k ∙ (–х) = –k х = –f(х).
При k > 0 функция возрастает, приk < 0 функция убывает.
Графиком прямой пропорциональности у=k х является прямая, проходящая через начало координат (еслиk> 0, то график расположен в первой и третьей четверти; еслиk< 0 – во второй и четвертой).
Свойство прямой
пропорциональности: если функция f(х) – прямая пропорциональность, и
(х1;у1), (х2;у2) – пары соответствующих
значений, причемх20, то![]() .
Действительно,у1=k
х1,у2=k
х2. Т.к.х20, тоу2 0. Тогда
.
Действительно,у1=k
х1,у2=k
х2. Т.к.х20, тоу2 0. Тогда![]() .
.
Если х> 0 иу > 0, то свойство прямой пропорциональности можно сформулировать так: с увеличением значений переменнойхв несколько раз соответствующее значение переменнойуувеличивается во столько же раз; с уменьшением значений переменнойхв несколько раз соответствующее значение переменнойууменьшается во столько же раз.
3. Обратная пропорциональность
Определение.
Обратной пропорциональностью называется
функция, заданная формулойу=![]() ,
гдеk 0. Числоk– коэффициент
обратной пропорциональности.
,
гдеk 0. Числоk– коэффициент
обратной пропорциональности.
Свойства функции
у=![]()
Область определения: (-
 ;
0)(0; +
;
0)(0; + )
)Множество значений: R\ {0}.
Функция нечетная, т.к. f(–х) =
 = –
= – = –f(х).
= –f(х).При k > 0 функция убывает на промежутке (-
 ;
0)(0; +
;
0)(0; + ),
приk < 0
функция возрастает на промежутке (-
),
приk < 0
функция возрастает на промежутке (- ;
0)(0; +
;
0)(0; + ).
).Графиком обратной пропорциональности является гипербола; при k > 0 график расположен в первой и третьей четверти, приk < 0 график расположен во второй и четвертой четверти. Чтобы построить график, надо составить таблицу значений функции.
Свойство обратной
пропорциональности: если функция f(х) – обратная пропорциональность,
и (х1;у1), (х2;у2) – пары соответствующих
значений, причемх20,у1 0, то![]() .
Действительно,у1=
.
Действительно,у1=![]() ,у2=
,у2=![]() .
Тогда
.
Тогда![]() .
.
Если х> 0 иу > 0, то свойство обратной пропорциональности можно сформулировать так: с увеличением значений переменнойхв несколько раз соответствующее значение переменнойууменьшается во столько же раз; с уменьшением значений переменнойхв несколько раз соответствующее значение переменнойуувеличивается во столько же раз.
4. Линейная функция
Определение. Линейной функцией называется функция, которую можно задать формулойу=k х+b, гдеk иb– некоторые действительные числа.
Если k= 0, то получаем постоянную функцию, еслиb= 0, то получаем прямую пропорциональностьу=k х.
Свойства:
Область определения – все действительные числа.
Множество значений – все действительные числа.
Функция не является ни четной, ни нечетной.
При k > 0 функция возрастает, приk < 0 функция убывает на всей числовой прямой.
Графиком линейной функции у=k х+bявляется прямая. Положение этой прямой на плоскости определяют коэффициентыk иb. Если k > 0, то угол между осью абсцисс и графиком функции острый, еслиk < 0, то угол тупой. Заметим, что чем больше модуль числаk, тем ближе прямая к оси ординат. Коэффициентbесть значение отрезка, отсекаемого прямой на оси ординат.
Пусть даны две линейные функции у=k1 х+b1 иу=k2 х+b2. Прямые, являющиеся графиками данных функций, пересекаются, еслиk1 k2; параллельны, еслиk1= k2; совпадают, еслиk1= k2иb1=b2.
5. Квадратичная функция
Определение. Квадратичной функцией называется функция, которую можно задать формулойу=ах2+bx+с, гдех– независимая переменная;а,b,с– некоторые числа, причема0.
Рассмотрим частный случай у=ах2. Графиком является парабола. Еслиа= 1, то формула примет виду=х2, и график проходит через точки (0; 0), (1; 1), (-1; 1), (2; 4), (–2; 4) (постройте график самостоятельно)
График функции у=ах2можно получить из графика функцииу=ах2сжатием к оси ординат, еслиа> 1 и сжатием к оси абсцисс, если 0 <а < 1.
Свойства функции у=ах2(а> 0):
Область определения – вся числовая прямая.
Множество значений [0; +
 )
)Функция четная.
Убывает на (–
 ;
0), возрастает на (0; +
;
0), возрастает на (0; + ).
).График – парабола, проходящая через точку (0; 0).
Наименьшее значение принимает в точке (0; 0), наибольшего значения нет.
График функции у= –х2получают из параболыу=х2путем осевой симметрии относительно оси абсцисс.
Рассмотрим функцию у=ах2+bx+с.
ах2+bx+с=а(х2+![]() х+
х+![]() )
=
)
=![]()
Получим формулу вида у=а(х – т)2+п.
Графиком является
парабола с вершиной в точке (т;п),
гдет=![]() ,п=
,п=![]() .
.
Осью симметрии является прямая х=т, параллельная оси ординат; если то ветви направлены вверх, еслиа< 0, то ветви направлены вниз.
Свойства квадратичной функции у=ах2+bx+с:
Область определения – вся числовая прямая.
Множество значений: при а> 0–
 ,
приа< 0–
,
приа< 0– 
Если b ≠ 0, то функция не является ни четной, ни нечетной.
При а> 0 убывает на (–
 ;
;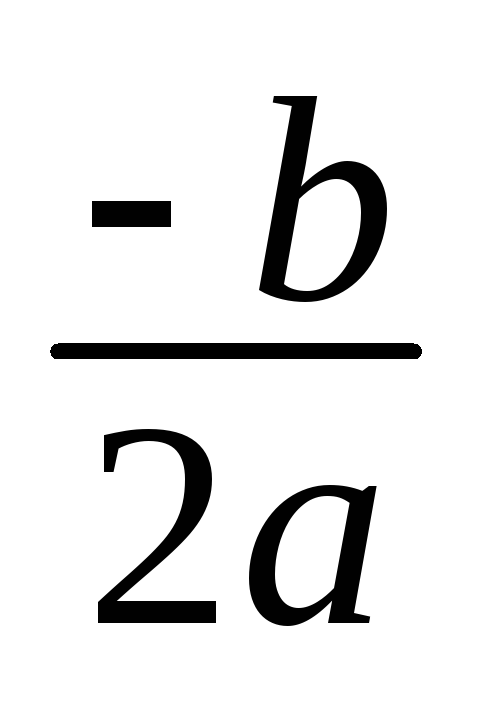 ), возрастает на промежутке (
), возрастает на промежутке ( ;
+
;
+ );
приа< 0 возрастает на промежутке
(–
);
приа< 0 возрастает на промежутке
(– ;
; ), убывает на промежутке (
), убывает на промежутке (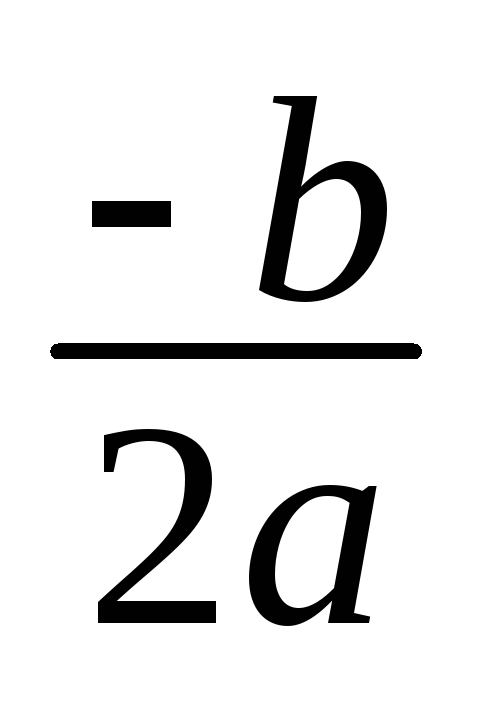 ;
+
;
+ ).
).
Примеры построения графиковквадратичных функций.
Первый способ.
Пусть требуется
построить график функции у=![]() х2+ 4х+ 5.
х2+ 4х+ 5.
Выполним
преобразования:
![]() х2+ 4х+ 5 =
х2+ 4х+ 5 =![]() (х2+ 8х+ 10) =
(х2+ 8х+ 10) =![]() (х2+ 8х+ 16 + 10 – 16) = =
(х2+ 8х+ 16 + 10 – 16) = =![]() (х+ 4)2– 3.
(х+ 4)2– 3.
Выполним параллельный
перенос плоскости, поместив начало
новой системы координат в точку О´(–
4; – 3) и построим в этой системе координат
график функцииу=![]() х2.
х2.
Можно было
воспользоваться формулами: х0 =![]() =
=![]() =
– 4;у0=
=
– 4;у0=![]() =
= .
.
Второй способ– построение параболы по точкам с ординатой, равной свободному члену квадратного трехчлена.
Пусть требуется построить график функции у=х2– 4х+ 5.
Найдем точки графика, имеющие ординату 5. для этого решим уравнение х2– 4х+ 5 = 5.
Имеем: х2– 4х= 0;х(х– 4) = 0, откудах1= 0;х2= 4.
Точки А(0; 5) иВ(4; 5) имеют одинаковую ординату, следовательно они симметричны относительно прямойх= 2. Еслих= 2, тоу= 4 – 8 + 5 = 1, т.е. вершина параболы имеет координаты (2; 1).
Третий способ– построение параболы по корням квадратного трехчлена.
Пусть х1их2= корни квадратного
трехчленаах2+bx+с, тогда график пересекает ось
абсцисс в точкеА(х1; 0) иВ(х2; 0), а ось симметрии
проходит перпендикулярно отрезкуАВчерез его середину, следовательно
абсциссу вершины находим по формулех0=![]() .
.
