Решение типовых задач

Пример 1. Для изучения оснащения заводов основными про­изводственными фондами было проведено 10%-ное выборочное обследование, в результате которого получены следующие данные о распределении заводов по стоимости основных производственных фондов:

Среднегодовая стоимость основных производственных фондов, млн. руб.	До 2	2 – 4	4 – 6	Свыше 6	Итого
Число заводов	5	12	23	10	50

Требуется определить: 1) с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться среднегодовая стоимость основных производственных фондов всех заводов генеральной совокупности; 2) с вероятностью 0,954 предельную ошибку выборки при определении доли и границы, в которых будет находиться удельный вес заводов со стоимостью основных производ­ственных фондов свыше 4 млн. руб.

Решение. Предельная ошибка выборки (ошибка репрезентативности) исчисляется по формуле:

,

где μ – средняя ошибка репрезентативности;

t – коэффициент кратности ошибки, показывающий, сколько средних ошибок содержится в предельной ошибке.

Пределы возможной ошибки (∆) определяются с вероятностью. Значение t найдем по таблице интеграла вероятностей.

Для Соответствует вероятность

t = 1 Р =0,683;

t = 2 Р =0,954;

t = 3 Р =0,997 и т. д.

Конкретное количественное выражение предельная ошибка принимает после определения средней ошибки выборки. Для нахождения ошибки репрезентативности собственно чайной и механической выборок имеются нижеследующие формулы.

Повторная выборка при определении:

среднего размера ошибки признака (1)

средней ошибки доли признака (2)

Бесповторная выборка при определении:

среднего размера ошибки признака 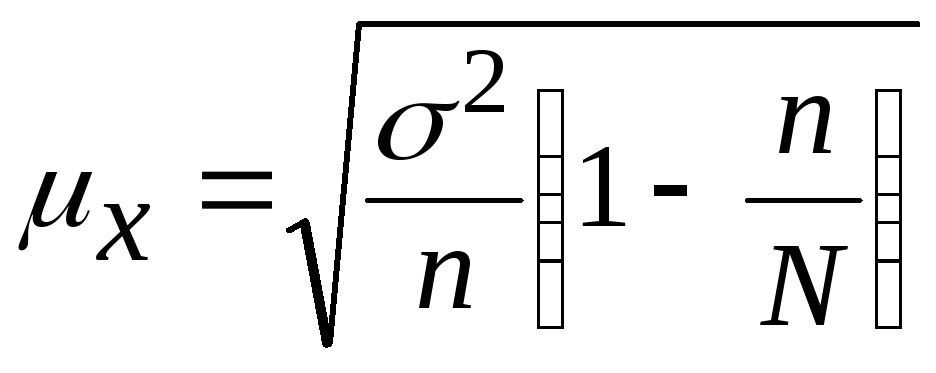(3)

средней ошибки доли признака (4)

N – численность генеральной совокупности;

п – численность выборочной совокупности;

² – дисперсия варьирующего (осредняемого) признака в выбороч­ной совокупности;

ω – доля данного признака в выборке;

(1 – ω) – доля противоположного признака в выборке.

1. Для определения границ генеральной средней необ­ходимо исчислить среднюю выборочную ()и дисперсию (²), техника расчета которых приведена в таблице:

Среднегодовая стоимость основных производственных фондов, млн. руб., х	Число заводов, f	Середина интервала, х	х f	х -	(х - )2	(х - )2 f
До 2	5	1	5	-3,52	12,39	61,95
2 – 4	12	3	36	-1,52	2,31	27,72
4 – 6	23	5	115	0,48	0,23	5,29
Свыше 6	10	7	70	2,48	6,15	61,50
	50		226			156,46

Тогда

млн. руб.;

.

Для упрощения расчетов средней и дисперсии можно использовать способ моментов. Техника расчетов и ² по способу моментов изложена в первой части брошюры «Прак­тикум по общей теории статистики».

Итак имеются данные: N = 500, п = 50 заводов; ² = 3,13.

Средняя ошибка выборки при определении среднегодовой .стоимости основных фондов составит:

а) при повторном отборе (по формуле 1) –

≈ ± 0,25 млн. руб.;

б) при бесповторном отборе (по формуле 3) –

≈ ± 0,24 млн. руб.;

Следовательно, при определении среднегодовой стоимости основных производственных фондов в среднем мы могли до­пустить среднюю ошибку репрезентативности в 0,25 млн. руб. при повторном и 0,24 млн. руб. при бесповторном от­боре в ту или иную сторону от среднегодовой стоимости ос­новных производственных фондов, приходящейся на один завод в выборочной совокупности. Исчисленные данные по­казывают, что при бесповторной выборке средняя ошибка репрезентативности (0,24) меньше, чем при тех же условиях при повторном отборе (0,25).

В нашем примере Р = 0,997, следовательно, t = 3.

Исчислим предельную ошибку выборочной средней (∆_х): ∆_х = ±3μ; т. е. ∆_х = = ±3 × 0,25 = ±0,75 млн. руб. (при повтор­ном отборе); ∆_х = ±3 × 0,24 = ±0,72 млн. руб. (при бесповторном отборе).

Порядок установления пределов, в которых находится средняя величина изучаемого показателя в генеральной со­вокупности в общем виде, может быть представлен следую­щим образом:

;

Для нашего примера среднегодовая стоимость основных производственных фондов в среднем на один завод генеральной совокупности будет находиться в следующих пределах.

а) при повторном отборе –

= 4,52 ± 0,25 или 4,27 млн. руб. ≤ ≤ 4,77 млн. руб.;

б) при бесповторном отборе –

= 4,52 ± 0,24 или 4,28 млн. руб. ≤ ≤ 4,76 млн. руб.

Эти границы можно гарантировать е вероятностью 0,997.

2. Вычисление пределов при установлении доли осуще­ствляется аналогично нахождению пределов для средней величины. В общем виде расчет можно представить следующим образом:

; ,

где р – доля единиц, обладающих данным признаком в генеральной совокупности.

Доля заводов в выборочной совокупности со стоимость основных производственных фондов свыше 4 млн. руб. со­ставляет:

, или 66%.

Определяем предельную ошибку для дели. По условию задачи известно, что N = 500; n = 5; ω = 0,66; Р = 0,954; t = 2.

Исчислим предельную ошибку доли:

при повторном отборе (по формуле 2) –

, или 13,4%;

при бесповторном отборе (по формуле 4) –

, или 12,7%.

Следовательно, с вероятностью 0,954 доля заведен се стоимостью основных производственных фондов свыше 4 млн. руб. в генеральной совокупности будет находиться в пределах:

р = 66% ± 13,4%, или 52,6% ≤ р ≤ 79,4% при повторном отборе;

р = 66% ± 12,7%, или 53,3% ≤ р ≤ 78,7% при бесповторном отборе.

Расчеты убеждают в том, что при бесповторном отборе ошибка выборки меньше, чем при тех же условиях при повторной выборке.

Пример 2. Используя данные предыдущей задачи, требуется ответить, каким должен быть объем выборочной совокупности при условии, что: 1) предельная ошибка выборки при определении среднегодовой стоимости основных производ­ственных фондов (с вероятностью 0,997) была бы не более 0,5 млн. руб.; 2) то же при вероятности 0,954; 3) предельная ошибка доли (с вероятностью 0,954) была бы не более 15%.

Решение. Для нахождения численности случайной и механической выборок имеются следующие четыре формулы:

Повторный отбор Бесповторный отбор

При определении

среднего размера

ошибки признака

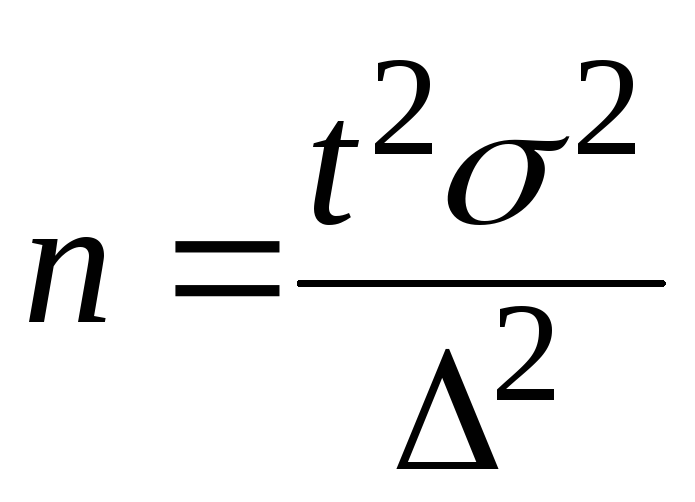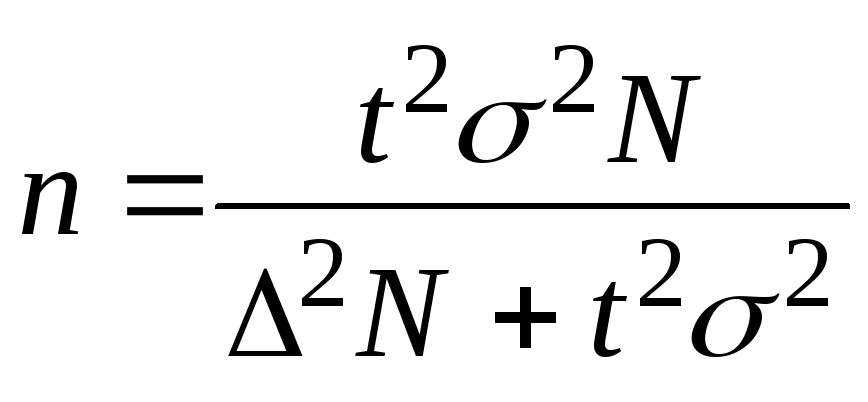(5); (6);

При определении

ошибки доли признака

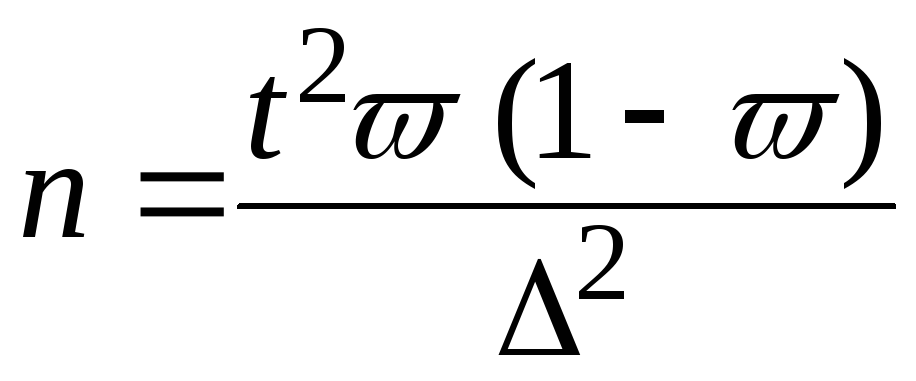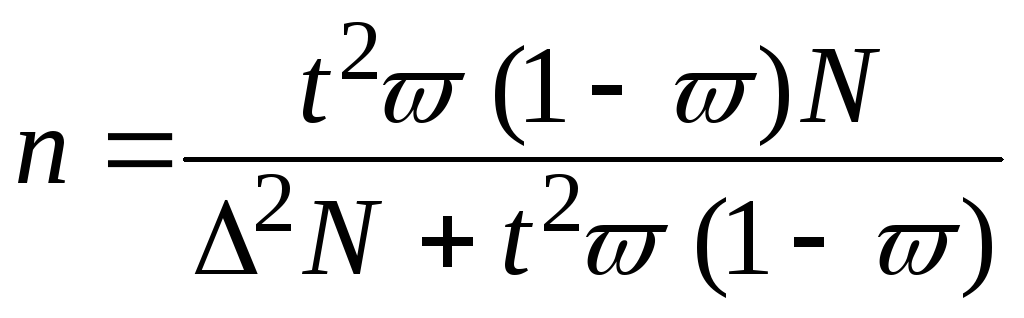(7); (8).

1) Известно, что N = 500; = 0,5 млн. руб.; ² = 3,13; Р = 0,997; t = 3.

Найдем объем выборки для расчета ошибки средней:

при повторном отборе (по формуле 5) –

заводов;

при бесповторном отборе (по формуле 6) –

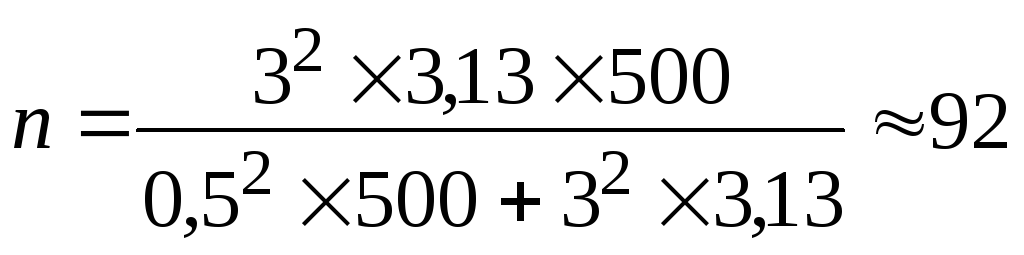завода.

2) Известно, что N = 500; = 0,5 млн. руб.; ² = 3,13; Р = 0,954; t = 2.

Определим объем выборки при бесповторном отборе (по формуле 6):

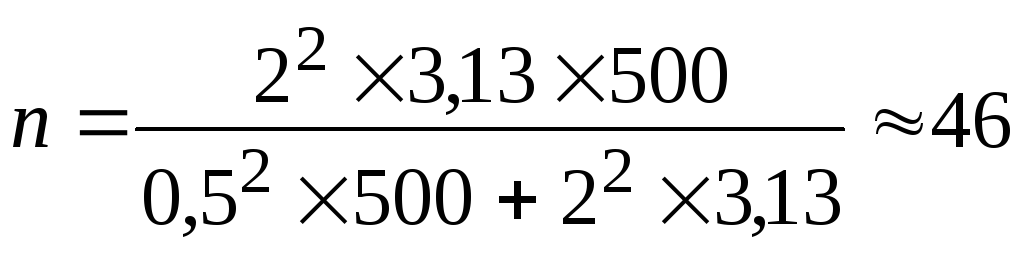завода.

3) Известно, что N = 500; = 0,5 млн. руб.; ω = 0,66; Р = 0,954; t = 2.

Объем выборки для расчета ошибки доли будет: при повторном отборе (по формуле 7) –

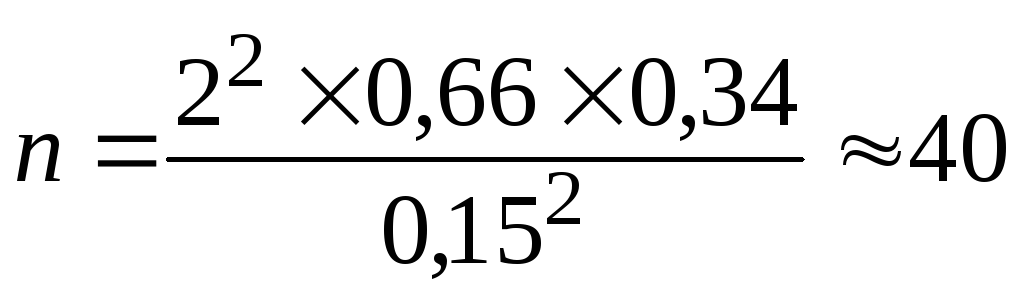заводов;

при бесповторном отборе (по формуле 8) –

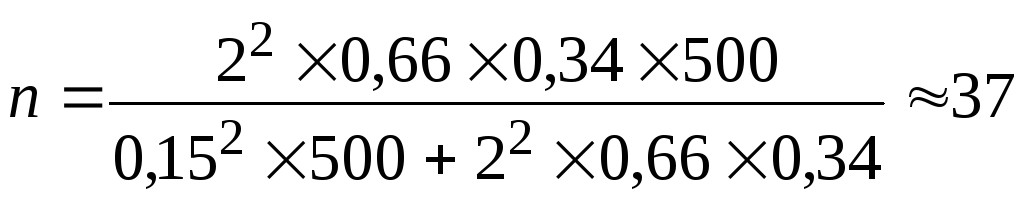заводов.

Выводы: 1) численность выборки увеличится, если при прочих равных условиях уменьшить предельную ошибку; 2) численность выборки уменьшится, если при прочих рав­ных условиях уменьшить вероятность, с которой требуется гарантировать результат выборочного обследования; 3) численность выборки уменьшится, если при прочих равных условиях увеличить предельную ошибку.

Пример 3. На заводе 1000 рабочих вырабатывают одноименную продукцию. Из них со стажем работы до пяти лет трудятся 400 чел., а более пяти лет – 600 чел. Для изучения среднегодовой выработки и установления доли квалифицированных рабочих проведена 10%-ная типическая выборка с отбором единиц пропорционально численности рабочих по указанным группам (внутри групп применялся случайный метод отбора).

На основе обследования получены следующие данные:

Группы рабочих со стажем работы	Общая численность рабочих, чел., N	Число обследованных рабочих, чел., п	Средне­дневная выработка, шт.,	Дисперсия выработки, Число	Число рабочих в выработке, чел., m	Доля рабочих,
До 5 лет (включ-но)	400	40	25	81	32	0,8
Свыше 5 лет	600	60	30	64	54	0,9
Итого	1000	100

Определим: 1) с вероятностью 0,954 предельную ошибку выработки и границы, в которых будут находиться среднедневная выработка всех рабочих завода; 2) с той же вероятностью пределы удельного веса квалифицированных рабочих в общей численности рабочих завода.

Решение. 1) Средняя ошибка типической выборки определяется по формуле:

(9)

где – средняя из внутригрупповых дисперсий.

Она исчисляется по формуле:

;

Тогда

.

Определим среднюю ошибку выборки при бесповторном отборе (по формуле 9) :

шт.

Техника расчета предельной ошибки при типической вы­борке аналогична вышеизложенному расчету предельной ошибки при случайном отборе:

или ;

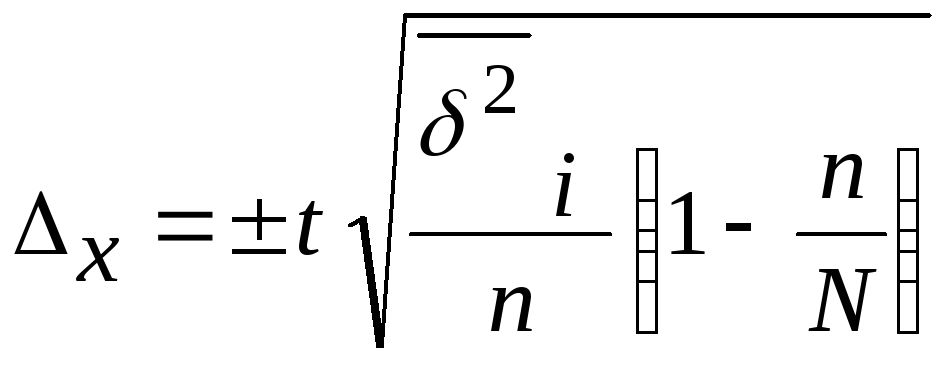Подставив данные, получим: = ± 2 × 0,83 = ± 1,6 шт.

Для определения возможных пределов среднедневной вы­работки всех рабочих завода первоначально нужно исчис­лить среднедневную выработку в выборочной совокупности по средней арифметической взвешенной:

шт.

Пределы среднедневной выработки всех рабочих завода: = 28 ± 1,6 шт.

С вероятностью 0,954 можно утверждать, что среднеднев­ная выработка всех рабочих завода находится в пределах 26,4 шт. ≤ ≤ 29,6 шт.

2) Средняя ошибка репрезентативности для доли исчис­ляется по формуле:

(10)

где – дисперсия доли () является средней из внутри групповых дисперсий.

Эта величина исчисляется по формуле:

Технику расчета покажем в таблице:

Группы рабочих со стажем работы	Числен­ность рабочих,	Доля квали­фициро­ванных рабочих,	Доля малоквалифицированных рабочих,	Дисперсия доли	Взвешенный показатель дисперсии,
До 5 лет	40	0,8	0,2	0,16	6,4
Свыше 5 лет	60	0,9	0,1	0,09	5,4
Итого	100				11,8

Тогда

.

Определим среднюю ошибку репрезентативности для доли (по формуле 10):

, или ± 3,2%.

Исчислим среднюю ошибку выборочной доли с вероятностью 0,954:

, или 6,4%.

Расчет предела при установлении доли в общем виде представляется следующим образом:

.

Определим среднюю долю для выборочной совокупности:

, или 86%.

Отсюда: р = 86% ± 6,4%.

Вывод: с вероятностью 0,954 можно утверждать, что доля квалифицированных рабочих на заводе будет находить­ся в пределах 79,6% ≤ р ≤ 92,4%.

Пример 4. С целью определения среднего эксплуатационного пробега 10000 шин легковых автомобилей, распределенных, на партии по 100 шт., проводится серийная 4%-ная бесповторная выборка. Результаты испытания отобранных шин характеризуются следующими данными:

Показатели	Партии
	1	2	3	4
Средний эксплуатационный пробег шин, тыс. км	40	42	45	48
Доля шин с пробегом не ме­нее 42 тыс. км	0,80	0,85	0,90	0,95

Определите: 1) средние ошибки репрезентативности: а) эксплуатационного пробега шин; б) удельного веса шин с пробегом не менее 42 тыс. км; 2) с вероятностью 0,954 пределы, в которых будет находиться: а) средний эксплуа­тационный пробег всех обследуемых шин; б) доля шин, про­бег которых не менее 42 тыс. км в генеральной совокупности.

Решение. 1) При бесповторном отборе серий средняя ошибка репрезентативности определяется по формулам:

для средней –

(11)

для доли –

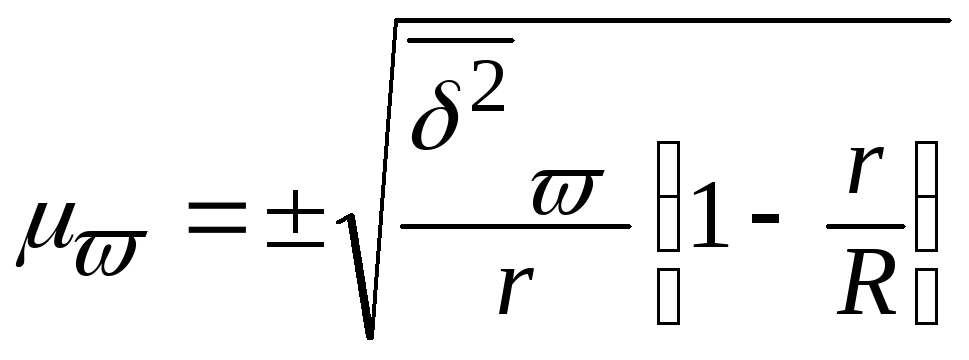(12)

где R – число серий в генеральной совокупности;

r – число отобранных серий;

– межсерийная дисперсия средних;

– межсерийная дисперсия доли.

Сначала исчислим обобщающие показатели.

Средний эксплуатационный пробег шин:

тыс. км.

Средний удельный вес шин с пробегом не менее 42 тыс. км равен:

(или 87,5%)

Межсерийная дисперсия определяется по формулам: для средней –

для средней –

;

для доли –

.

Для ее расчета построим вспомогательную расчетную таб­лицу:

№ партии	Средний пробег шин, тыс. км.,			Доля шин с пробегом не менее 42 тыс. км.,
1	40	-3,75	14,06	0,8	-0,075	0,005625
2	42	-1,76	3,06	0,85	-0,025	0,000625
3	45	1,25	1,56	0,90	0,025	0,000625
4	48	4,25	18,06	0,95	0,075	0,005625
Итого			36,74			0,012500

Тогда

; .

Определим средние ошибки репрезентативности:

для средней (по формуле 11) –

тыс. км.;

для доли (по формуле 12) –

, или ± 2,74%.

2) Определим с вероятностью 0,954 предельные ошибки репрезентативности для средней и для доли:

тыс. км.;

%.

Отсюда средний эксплуатационный пробег всех обсле­дуемых шин будет находиться в пределах:

= ± = 43,75 ± 3,0, или 40,75 тыс. км ≤ х ≤ 46,75 тыс. км.

Средний удельный вес шин с пробегом не менее 42 тыс. км в генеральной совокупности будет находиться в пределах:

p = ± = 87,5% ± 5,5%, или 82,0% ≤ р ≤ 93,0%.

Пример 5. Используя условие и решение предыдущей задачи, определите вероятность того, что: а) предельная ошибка выборки при установлении среднего эксплуатационного про­бега шин не превышает 4,0 тыс. км; б) доля шин с пробегом не менее 42 тыс. км будет находиться в пределах от 83% До 92%.

Решение. При определении вероятности используется формула предельной ошибки:

.

В нашем примере следует использовать формулу пре­дельной ошибки серийного отбора.

а) Дано: R = 100; r = 4; = 43,75 тыс. км; = 9,185; = 4,0 тыс. км.

Требуется определить вероятность того, что разница сред­них величин эксплуатационного пробега шин в выборочной и генеральной совокупности не превысит ± 4,0 тыс. км, т. е.

р | – | ≤ 4,0 тыс. км.

Подставляем данные в формулу:

;

;

.

По таблице значений вероятностей находим, что при t = 2,67 вероятность будет 0,992.

Следовательно, с вероятностью 0,992 можно гарантиро­вать, что средний эксплуатационный пробег шин легковых автомобилей в генеральной совокупности будет находиться в пределах 39,75 тыс. км ≤ ≤ 47,75 тыс. км;

б) Дано: R = 100; r = 4; = 87,5%; = 0,003125; = 4,5%.

Требуется определить: p | –р | ≤ 4,5%, т. е. вероятность того, что доля шин с пробегом не менее 42 тыс. км в вы­борочной совокупности не будет отклоняться от доли гене­ральной совокупности более чем на 4,5%.

Подставив данные в формулу

(см. решение выше), получим 4,5% = t × 2,74%;

, тогда Р = 0,899.

Следовательно, вероятность того, что удельный вес шин с пробегом не менее 42 тыс. км будет находиться в преде­лах от 83% до 92%, равна 0,899.