Решение

1. Для вычисления параметров модели следует воспользоваться формулами (3.2.16). Промежуточные расчеты приведены в таблице 3.2.4.

Табл. 3.2.4.

,

= 2329,06+0,85* 2539,24=170,47.

В матричной форме расчет параметров модели может быть представлен следующим образом:

Построена модель зависимости расходов от дохода:

.

При увеличении дохода на 1 руб. расходы увеличиваются в среднем на 0,85 руб.

2) Расчетное значение t- критерия () вычислим по формулам (3.2.27) и (3.2.28), используя данные таблицы 3.2.4.

где === 137,19

Табличное значение t-критерия при 10% уровне значимости и степенях свободы (17-1-1=15) составляет 1,75. Так как |t|>t, то коэффициентзначим.

3) Доверительный интервал для прогнозов индивидуальных значений определяется из соотношения:

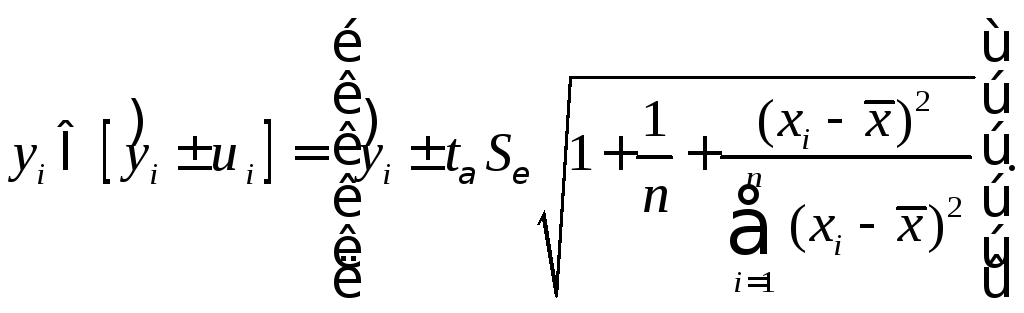
Величину отклонения от линии регрессии вычисляют по формуле (3.2.26), используя данные таблицы 3.2.4.

Коэффициент Стьюдента дляm=15 степеней свободы (m=n-2) и уровня значимости 0,05 равен 2,13.

Результаты вычислений приведены в табл. 3.2.5 и на рис. 3.2.5.

Табл. 3.2.5.

		верхняя граница	нижняя граница
1	303,73	2840,86	2233,40
2	304,71	2392,14	1782,72
3	311,52	2234,88	1611,84
4	300,91	2641,67	2039,85
5	340,60	1866,97	1185,77
6	304,73	2391,32	1781,85
7	302,24	2488,28	1883,81
8	300,92	2611,93	2010,09
9	302,84	2804,27	2198,59
10	335,41	3409,80	2738,99
11	300,90	2630,61	2028,81
12	300,94	2605,14	2003,27
13	305,25	2892,53	2282,04
14	301,46	2722,98	2120,06
15	306,18	2350,26	1737,89
16	300,92	2648,48	2046,64
17	327,95	3313,08	2657,18

Рис.3.2.5. График исходных данных, результаты моделирования и доверительные интервалы.

4) Для того, чтобы определить расходы при доходе 3600 руб. необходимо получить точечный и интервальный прогноз аналогично п.2. Для этого следует подставить значение равное 3600 в полученную модель

Y_{прогноз}=170,47 +0.85*36003230,81.

U_{(x=3600 ,n=15,=0.1)} =

Таким образом, прогнозное значение =3230,81cвероятностью 90% будет находиться между верхней границей, равной 3230,81 +265,49=3496,30 и нижней границей, равной 3230,81 -265,49=2965,32.

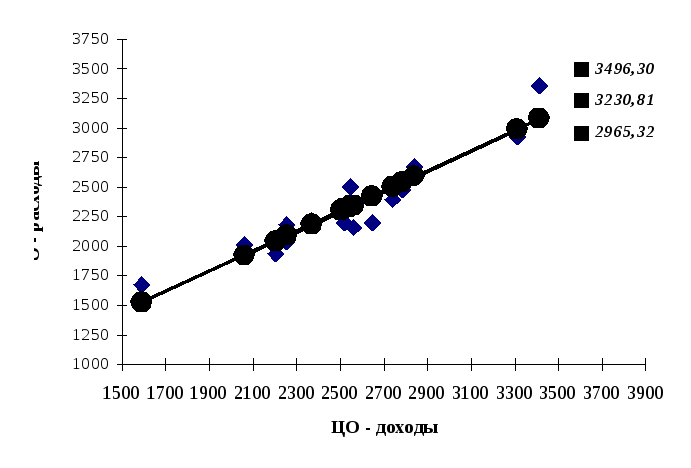
Рисунок 3.2.6. График модели парной регрессии зависимости расходов от дохода, точечный и интервальный прогноз при x= 3600.

3.3.4. Нелинейная регрессия

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам:

• регрессии, нелинейные по оцениваемым параметрам.

Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам

Данный класс нелинейных регрессий включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером могут служить:

полиномы разных степеней

(полином k-й степени)

и равносторонняя гипербола

.

При оценке параметров регрессий нелинейных по объясняющим переменным используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной регрессии. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

Первый пример построения модели нелинейной регрессии.

Используя данные примера 3.2.4, построим модель зависимости объёма выпускаемой продукции от температуры при технологическом процессе с помощью полинома второй степени (парабола второй степени): . Заменяя переменную х² на новую переменную z, получим двухфакторное уравнение линейной регрессии: , для оценки параметров которого используется обычный МНК.

На рис. 3.3.8. приведен график регрессионной модели, построенной на основании данных, примера 3.2.3.

Рис. 3.3.8. График модели регрессии .

Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.

Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Равносторонняя гипербола, для оценки параметров которой используется тот же подход «замены переменных» (1/x заменяют на переменную z) хорошо известна в эконометрике.

Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса² и Энгеля³.

Второй пример построения модели нелинейной регрессии.

Табл. 3.3.10.

Темпы инфляции (Y)	1	1,1	1,2	1,3	1,7	2,9	2,9	4,2	5,4
Норма безработицы4 (X)	6,5	5,4	5,5	5	4,4	3,7	3,7	3,5	3,4

Построим диаграмму рассеяния для переменных X (процент безработных в общей численности рабочей силы) иY (темп инфляции) на основании данныхтабл. 3.3.10.

Характер диаграммы рассеяния (рис.3.3.9) явно указывает на наличие нелинейной связи между рассматриваемыми переменными. Изображенная на диаграмме прямая , подобранная методом наименьших квадратов, очевидным образом не соответствует характеру статистических данных, хотя значение коэффициента детерминациии представляется достаточно высоким.

Рис. 3.3.9. Диаграмма рассеяния.

В связи с этим, при подборе моделей к реальным статистическим данным следует обращать внимание не только на коэффициент детерминации, но и (обязательно!) на соответствие подобранной модели характеру статистических данных.

Поскольку, на первый взгляд, расположение точек напоминает график обратной пропорциональной зависимости, рассмотрим модельравносторонней гиперболы

,

соответствующую линейной связи между переменными Y и . Подбор такой связи междунормой безработицы темпом инфляцииметодом наименьших квадратов приводит к модели

с достаточно высоким коэффициентом детерминации (Рис. 3.3.10а).

На практике подбор наилучшей модели регрессии выполняют с помощью специальных программных продуктов таких как STATISTICA,SSPS,VSTAT,CТАТЭКСПЕРТ и др.

Использование программного продукта CТАТЭКСПЕРТ позволило получить модель

с еще большим коэффициентом детерминации (Рис. 3.3.10б). График модели свидетельствует о хорошем соответствии подобранной модели характеру статистических данных.

Рис. 3.3.10. Графики двух регрессионных моделей

а)( )

иб)( ).

Регрессии нелинейные по оцениваемым параметрам

К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:

• степенная - ;

• показательная - ;

• экспоненциальная -

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен: ,где у — спрашиваемое количество; х — цена;

Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду . Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.

Широкое использование степенной функции связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.

Третий пример построения модели нелинейной регрессии.

По 12 областям регионаполучена информация, характеризующая зависимостьпотребительских расходов (Y,. руб.) отденежных доходов ( Х, руб. ).

Табл. 3.3.11.

Номер региона	Потребительские расходы на душу населения, руб. Y	Денежные доходы на душу населения, руб.Х
1	190	560
2	210	620
3	230	620
4	240	690
5	255	760
6	300	880
7	330	1000
8	330	1100
9	365	1200
10	370	1350
11	380	1400
12	410	1500

Для характеристики Yот Х требуется:

1. Построить степенную модель:

2.Оценить модель, определив:

• индекс корреляции,

• среднюю относительную ошибку,

• коэффициент детерминации,

• F-критерий Фишера.

2. Результаты расчетов отобразить на графике.