Всероссийский заочный финансово-экономический институт

КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ

Эконометрика

Тема 3. Парная регрессия и корреляция.

(Материалы к лекции)

Орлова и.В.

2005

Вопросы по теме лекции

• Статистическая зависимость (независимость) случайных переменных. Ковариация, корреляция.

• Анализ линейной статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции.

• Статистическая зависимость (независимость) случайных переменных. Ковариация.

• Предпосылки метода наименьших квадратов.

• Свойства оценок МНК.

• Линейная модель парной регрессии. Оценка параметров модели с помощью метода наименьших квадратов (МНК).

• Оценка качества модели парной регрессии.

• Проверка выполнения предпосылок МНК.

• Интервалы прогноза по линейному уравнению парной регрессии.

• Нелинейная регрессия. Нелинейные модели и их линеаризация.

• Проверка условия гомоскедастичности.

• Гетероскедастичность и способы устранения.

Материалы к лекции по теме Парная регрессия и корреляция содержат примеры из учебного пособия И.В. Орловой

Пример 3.2.1.Вычисление коэффициентов парной, множественной и частной корреляции.

В табл. 3.2.2 представлена информация об объёмах продаж и затратах на рекламу одной фирмы, а также индекс потребительских расходов за ряд текущих лет.

Требуется:

1. Построить диаграмму рассеяния (корреляционное поле) для переменных «объёмы продаж» и «индекс потребительских расходов».

2. Определить степень влияния индекса потребительских расходов на объёмы продаж (вычислить коэффициент парной корреляции).

3. Оценить значимость вычисленного коэффициента парной корреляции.

4. Построить матрицу коэффициентов парной корреляции по трем переменным.

5. Найти оценку множественного коэффициента корреляции.

6. Найти оценки коэффициентов частной корреляции.

Таблица 3.2.2

Объем продаж, тыс. руб.-Y	126	137	148	191	274	370	432	445	367	367	321	307	331	345	364	384
Затраты на рекламу - Х1	4	4,8	3,8	8,7	8,2	9,7	14,7	18,7	19,8	10,6	8,6	6,5	12,6	6,5	5,8	5,7
Индекс потребительских расходов, % - X2	100	98,4	101,2	103,5	104,1	107	107,4	108,5	108,3	109,2	110,1	110,7	110,3	111,8	112,3	112,9

Решение

1) Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение о том, что существует некоторая объективная тенденция прямой линейной связи между значениями переменных x-индекс потребительских расходов иy-объёмы продаж.

В нашем примере диаграмма рассеяния имеет вид, приведенный на рис 3.2.1.

2) Промежуточные расчеты при вычислении коэффициента корреляции между переменными x-индекс потребительских расходов иy-объёмы продаж приведены в таблице 3.2.3.

Средние значения случайных величин Х и Y, которые являются наиболее простыми показателями, характеризующими последовательностии, рассчитаем по формулам, соответственно:

.

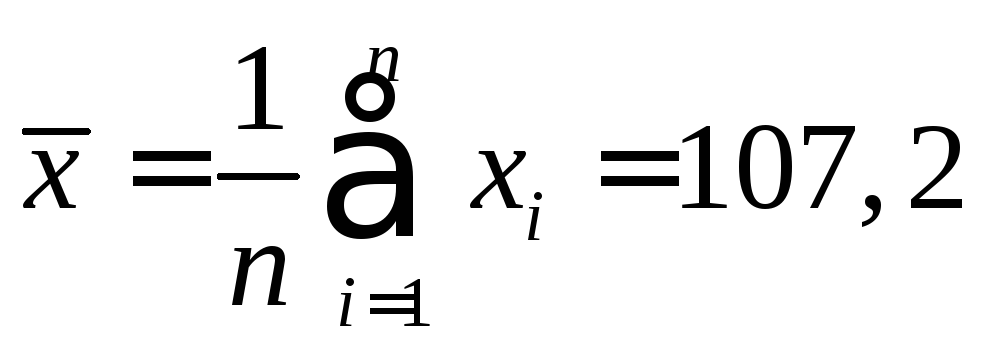
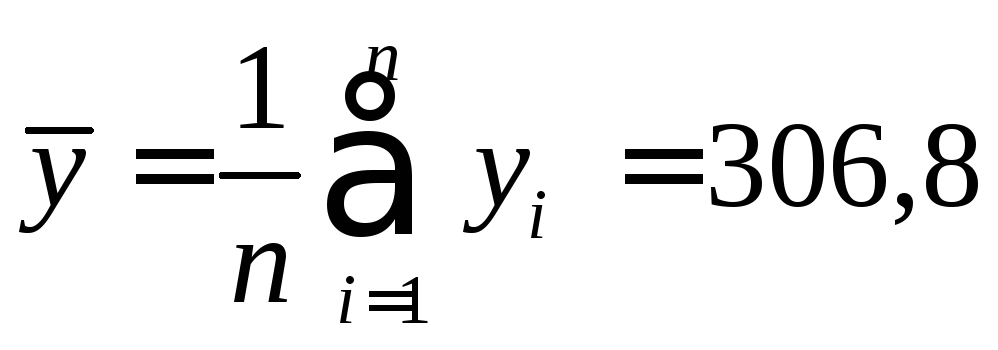Дисперсия характеризуют степень разброса значений () вокруг своего среднего(, соответственно)

Рис. 3.2.1. Диаграмма рассеяния.

Стандартные ошибки случайных величин Х и Y рассчитаем по формулам, соответственно:

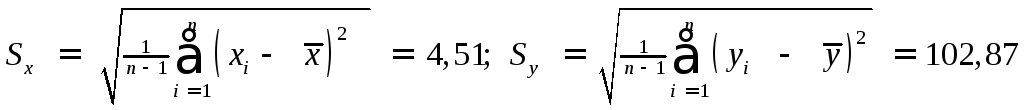
Коэффициент корреляции рассчитаем по формуле (3.2.2), используя данные из таблицы 3.2.3:

Таблица 3.2.3.

№	Y	X
1	126	100	-180,813	-7,231	1307,500	52,291	32693,160
2	137	98,4	-169,813	-8,831	1499,657	77,991	28836,285
3	148	101,2	-158,813	-6,031	957,838	36,376	25221,410
4	191	103,5	-115,813	-3,731	432,125	13,922	13412,535
5	274	104,1	-32,813	-3,131	102,744	9,805	1076,660
6	370	107	63,188	-0,231	-14,612	0,053	3992,660
7	432	107,4	125,188	0,169	21,125	0,028	15671,910
8	445	108,5	138,188	1,269	175,325	1,610	19095,785
9	367	108,3	60,188	1,069	64,325	1,142	3622,535
10	367	109,2	60,188	1,969	118,494	3,876	3622,535
11	321	110,1	14,188	2,869	40,700	8,230	201,285
12	307	110,7	0,188	3,469	0,650	12,032	0,035
13	331	110,3	24,188	3,069	74,225	9,417	585,035
14	345	111,8	38,188	4,569	174,469	20,873	1458,285
15	364	112,3	57,188	5,069	289,869	25,692	3270,410
16	384	112,9	77,188	5,669	437,557	32,135	5957,910
сумма	4909	1715,7	0,000	0,000	5681,994	305,474	158718,438
среднее	306,8125	107,23125

3) Оценим значимость коэффициента корреляции. Для этого рассчитаем значение t –статистики по формулеТабличное значение критерия Стьюдента равно:t_табл (α = 0,1;k = n– 2 = 14) =1,76 (см. Приложение 2). Сравнивая числовые значения критериев, видно, чтоt_расч > t_табл, т.е. полученное значение коэффициента корреляции значимо.

Таким образом, индекс потребительских расходов оказывает весьма высокое влияние на объёмы продаж.

4) Матрица R коэффициентов парной корреляции, вычисленных по формуле (3.2.2) для трех факторов будет иметь вид:

		Объем реализации	Затраты на рекламу	Индекс потребительских расходов
		1	2	3
Объем реализации	1	1	0,646	0,816
Затраты на рекламу	2	0,646	1	0,273
Индекс потребительских расходов	3	0,816	0,273	1

5) Вычисление множественного коэффициента корреляции y c x1 и x2.

- определитель корреляционной матрицы R равен 0,1304 (см. главу 1, 1.2),

- алгебраическое дополнение 1-го диагонального элемента той же матрицы R

.

6) Вычисление коэффициентов частной корреляции.

,

где алгебраическое дополнение элемента матрицы R, а алгебраическое дополнение 2-го диагонального элемента:

.

Коэффициенты частной корреляции можно вычислить, используя коэффициенты парной корреляции:

.