
- •Всероссийский заочный
- •2. Определители 2-го и 3-го порядков(определение и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца
- •Свойства определителей
- •Теорема Лапласа о разложении определителя по элементам строки или столбца
- •3. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления
- •4. Понятие минора k-го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований
- •5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы
- •Тема 2: Системы линейных уравнений
- •7. Решение системы n линейных уравнений с n переменными по формулам Крамера
- •8. Решение системы n линейных уравнений с n переменными
- •9. Метод Гаусса решения системы n линейных уравнений с n переменными. Понятие о методе Жордана-Гаусса
- •10. Система m линейных уравнений с n переменными. Теорема Кронекера-Капелли. Условия определенности и неопределенности совместной системы линейных уравнений
- •11. Базисные (основные) и свободные (неосновные) переменные системы m линейных уравнений с n переменными. Базисное решение
- •12. Система линейных однородных уравнений и ее решения. Условие существования ненулевых решений системы
- •Тема 3: Векторные пространства
- •13. Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами (сложение, умножение вектора на число). Коллинеарные и компланарные векторы
- •14. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами
- •16. Векторное (линейное) пространство, его размерность и базис. Теорема о существовании и единственности разложения вектора линейного пространства по векторам базиса
- •17. Скалярное произведение векторов в n-мерном пространстве. Евклидово пространство. Длина (норма) вектора
- •17. Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса в евклидовом пространстве
- •Тема 4: Линейные операторы
- •19. Определение оператора. Понятие линейного оператора. Образ и прообраз векторов
- •20. Матрица линейного оператора в заданном базисе: связь между вектором х и образом у. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы
- •21. Собственные векторы и собственные значения матрицы. Собственные векторы и собственные значения оператора (матрицыА). Характеристический многочлен оператора и его характеристическое уравнение
- •22. Матрица линейного оператора в базисе,
- •24. Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм
- •25. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра)
- •Тема 6: Элементы аналитической геометрии
- •26. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести)
- •27. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых
- •28. Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса
- •29. Канонические уравнения гиперболы и параболы, геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратно пропорциональной зависимости и квадратного трехчлена
- •30. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей
- •42. Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условия параллельности и перпендикулярности двух плоскостей, двух прямых, прямой и плоскости
5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.
Пусть дана матрица
 .
Для ее строк введем обозначения:e1=(a11,
a12,
... , a1n),e2=(a21,
a22,
... , a2n),
...,em=(am1,
am2,
... , amn).
.
Для ее строк введем обозначения:e1=(a11,
a12,
... , a1n),e2=(a21,
a22,
... , a2n),
...,em=(am1,
am2,
... , amn).
Две строки матрицы называются равными, если равны их соответствующие элементы.
Операции умножения строки на число и сложения строк вводятся как операции проводимые поэлементно.
Определение 1. Строкаеназываетсялинейной комбинациейстрокe1,e2, ... ,es, матрицы, еслие=1e1+2 e2+ ... +s es, где1,2, ... ,s- произвольные числа.
Определение 2. Строки матрицыe1,e2, ... ,esназываютсялинейно зависимыми, если существуют такие числа1,2, ... ,sне равные нулю одновременно, что линейная комбинация1e1+2e2+ ... +sesравна нулевой строке.
Линейная зависимость всех строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных строк.
Определение 3. Строки матрицыe1,e2, ... ,esназываютсялинейно независимыми, если их линейная комбинация1e1+2e2+ ... +sesравна нулевой строке тогда и только тогда, когда все коэффициенты1,2, ... ,sравны нулю.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов,через которые линейно выражаются все остальные ее строки (столбцы).
Тема 2: Системы линейных уравнений
6. Система n линейных уравнений с n переменными (общий вид) и матричная форма её записи. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений
Определение 1. Системой n линейных уравнений с n переменныминазывается система вида:
 ,
,
где aij(i=1,2,...,n;j=1,2,...,n) - коэффициенты при переменных;
bi(i=1,2,...,n) - свободные члены.
Запишем систему линейных уравнений в матричной форме.
Обозначим
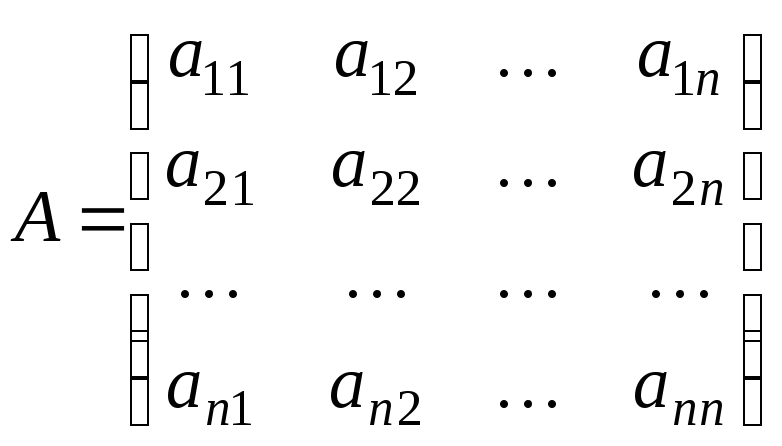 ;
;
 ;
; .
.
Имеем
 - матрица-столбец. Следовательно,
по определению равенства матриц, систему
уравнений можно записать в видеAX=B, гдеA-матрица
коэффициентов при переменных,Х-матрица столбец переменных,B-матрица-столбец свободных членов.
- матрица-столбец. Следовательно,
по определению равенства матриц, систему
уравнений можно записать в видеAX=B, гдеA-матрица
коэффициентов при переменных,Х-матрица столбец переменных,B-матрица-столбец свободных членов.
Определение 2. Решением системы уравненийназывается такой упорядоченный набор (k1,k2, ... ,kn) чисел, при подстановке которых вместо переменныхx1,x2, ... ,xnкаждое уравнение системы обращается в верное числовое равенство.
Определение 3. Система уравнений называетсясовместной, если она имеет хотя бы одно решение.
Определение 4. Система уравнений называетсянесовместной, если она не имеет решений.
Определение 5. Совместная система уравнений называетсяопределенной, если она имеет единственное решение.
Определение 6. Совместная система уравнений называетсянеопределенной, если она имеет более одного решения.
Определение 7. Две системы уравнений называютсяравносильнымиилиэквивалентными, если они имеют одно и то же множество решений.
7. Решение системы n линейных уравнений с n переменными по формулам Крамера
Пусть дана система двух линейных уравнений с двумя переменными:
 .
.
Умножим первое уравнение на a22, второе уравнение на (-a12) и сложим их. Получим уравнение (a11a22-a21a12)x1=b1a22-b2a12.
Умножим первое уравнение на (-a21), второе уравнение наa11и сложим их. Получим уравнение (a11a22-a21a12)x2=a11b2-a21b1.
Заметим, что ![]() ,
,
![]() ,
,![]()
т.е. система имеет вид
 .
.
Если 0, то система
имеет единственное решение![]() ,
,![]() .
.
Если =0, а10 или20 то система несовместная.
Если =0,1=0 и2=0 , то система неопределенная и имеет бесконечное множество решений.
Теорема Крамера. Пусть- определитель матрицыAсистемыnлинейных уравнений сnпеременными,j- определитель матрицы, полученной из матрицыAзаменойj-го столбца столбцом свободных членов (j=1,2,...,n). Тогда, если0, то система имеет единственное решение, определяемое по формулам
![]() ,
,
![]() ,
. . . ,
,
. . . ,
![]() (формулы Крамера).
(формулы Крамера).
