Уравнение плоскости.

П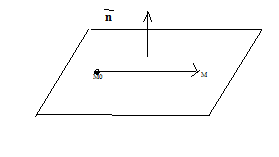усть плоскость проходит точку М₀(х₀,y₀,z₀) перпендикулярно вектору . М(х,y,z)-текущая точка плоскости. . Тогда,или

А(х-х₀) + В(y-y₀)+C(z-z₀)=0 (16)

Уравнение (16) запишем в виде:

Ах+Вy+Сz+D=0 (17)

где D=-Ах₀-Вy₀-Cz₀.

Если D=0: Ах+Вy+Сz=0- плоскость, проходящую через начало координат.

А=0: Вy+Сz+D=0-плоскость, параллельной оси Ох.

А=D=0:Вy+Сz=0-плоскость, проходящею через ось Ох.

А=В=0:Сх+D=0-плоскость, параллельной плоскости Охy.

А=В=D=0:Сz=0-координатная плоскость Охy.

Условия параллельности и перпендикулярности плоскостей векторов и:-условия параллельности плоскостей.

А₁А₂+В₁В₂+С₁С₂=0 – условия перпендикулярности плоскостей.

Прямая в пространстве задается как линия пересечения двух плоскостей:

Уравнение -каноническое уравнение прямой в пространстве. Определяется из условия коллинеарности векторови(m,n,p)-направляющий вектор прямой.

Под углом между двумя плоскостями понимается угол между их нормалями () и:

(18)

Угол между прямыми есть угол между направляющими векторами этих прямых:

(19)

Угол между прямой и плоскостью определяется через - направляющий вектор прямой и- вектор нормали плоскости по формуле:

(20).