Решение:

А₁₁= 4, а₂₂= 1_, а₃₃= -3, а₁₂= а₂₁ = -6, а₁₃ = а₃₁= -5, а₂₅= 0

L = (х₁, х₂, х₃)

Рассмотрим невырожденном линейном преобразовании переменных. Пусть Х= (х₁, х₂, х₃) и Y= (y₁, y₂,….,y_n) связаны линейным соотношением Х=СY, где С=(С_ij)- есть некоторая невырожденная матрица n-го порядка. Тогда:

, т.е. при невырожденном линейном преобразовании Х=СY матрица квадратичной формы принимает вид:

А^*=(3)

Квадратичная форма называется канонической, если все ее коэффициенты а_ij=0 при i≠j

, а ее матрица является диагональной.

Теорма: Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Канонические формы имеет ряд общих свойств. Одно из этих сформулируем в виде.

Теорема(закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

Рангом квадратичной формы называется ранг матрицы квадратичной формы. Ранг равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичная форма L-называется положительно (отрицательно) определенной, если при всех значениях переменных.

L(х₁,х₂,...,х_n)>0 (L(х₁,х₂,…,х_n)<0).

Теорма. Для того чтобы квадратичная форма L=была положительно (отрицательно) определенной, необходимо и достаточно, чтобы ее собственные значенияλ _i матрицы А были положительны (отрицательные).

Для знакоопределенности квадратичной формы используется и следующая теорема.

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и недостаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е.

>0, > >0,…,_n>0, где

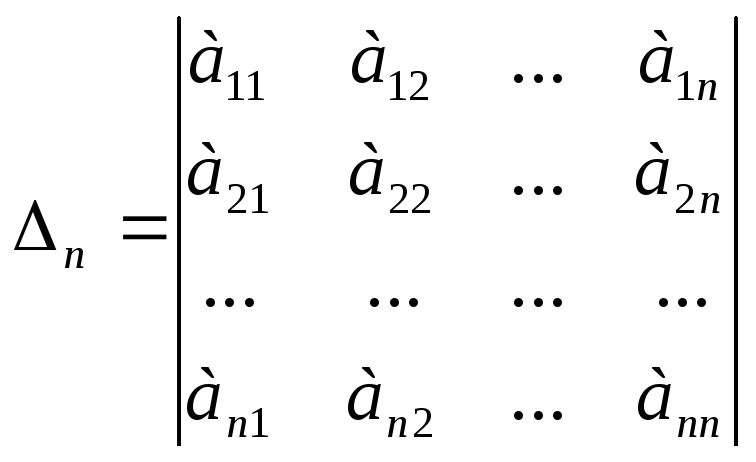
Замечание. Для отрицатель определенных квадратичных форм знаки главных миноров чередуются.

Тема 6. Элементы аналитической геометрии. (3+1ч.).

Пусть имеем на плоскости координат некоторую линию.

Определение. Уравнением линии на координатной плоскости 0_хy называется уравнение, которому удовлетворяют координаты х и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Y= f(х), а М (х,y)-текущая точка линии.

Уравнение прямой

И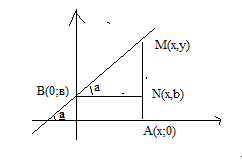зМNB: tq а = (1)

Пусть k = tq a, получим k = илиy = kх+b (2)

Уравнение (2) –уравнение с угловым коэффициентом. Пусть M₁(х₁y₁) – тогда, принадлежащий прямой. Тогда y₁ = kх₁ + b.

Вычитая из уравнения (2) получим:

y-y₁ = k (х-х₁) (3)

Уравнение (3) – уравнение прямой, проходящий через данную точку в данном направлении.

Пусть М₂ (х₂,y₂) лежит на данной прямой. Тогда, подставляя ее координаты в (3), получаем:

y₂ –y₁ = или

(5)

( 5) – уравнение прямой, проходящей через две данные точки.

Общее уравнение прямой.

Уравнение (2) и (5) представляет собой уравнения первой степени с двумя переменами. Такое уравнение в общем виде можно записать в виде:

(6)

1. Пусть В≠0. Тогда y=. Если k = , В =, тоy=kх+b – уравнение прямой с угловым коэффициентом. Если А≠0, С=0, то y = kх – уравнение прямой, проходящей через начало координат. Если А=0, С≠0, то y=b – уравнение прямой, параллельной оси О_y. Если А =0, С=0, то y=0 – уравнение оси О_х^.

2. Пусть В=0, А≠0, то х=или х=а, где а=- уравнение прямой, параллельной оси О_y.

Уравнение (6) называется общим уравнением прямой.

Прямая на плоскости

Для нахождения точки пересечения двух прямых нужно решить систему.

Если прямые не параллельны, то получим единственную точку.

=а₂-а₁ и y=k₁х+b₁

y=k₂х+b₂

k₁=tq а₁, k₂=tq а₂

tq =tq (а₂-а₁) =

tq= (7)

Если прямые параллельны, то =0. Из ( 7) получим k₁=k₂ – необходим и достаточным условием параллельности двух прямых.

Если прямые перпендикулярны, то =иtq не определен, а ctq и 1+k₁k₂=0 или k₁k₂=-1.

Для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку. Для обозначения вида l₁ || l₂ : и условие перпендикулярности А₁А₂+В₁В₂=0.

Кривым второго порядка описывается уравнение второй степени с двумя переменами, имеющий общий вид:

Ах²+Вхy+Сy²+Дх+Еy+F=0 (8)

Пусть данная окружность с центром О^` (х_о,y_о) и радиусом R. Тогда ОМ=R.

(х-х₀)²+(y-y₀)²=R² (9)

Уравнение (9) называется нормальным уравнением окружности. Если центр совпадает с началом координат.

х² + y² = R² (10)

Преобразование уравнение (8) можно представить к виду:

Ах² + Сy² = b (11)

Кривая второго порядка (11) называется эллипсом, если коэффициента А и С имеют одинаковые знаки.

(12) где

Уравнение (12) –каноническое уравнение эллипса. Кривая (11) называется гиперболой, или А и С имеют противоположные знаки ( А>0, С<0) и b>0.

Каноническое уравнение гиперболы имеет вид:

(13)

Где а=-действительная полуось,b=-мнимая полуось.

F₁(c,0) и F₂(-c,0)-фокусы

Прямые y=-асимптотами гиперболы.

Уравнение (8) В=0, А=0, С≠0, т.е.

Сy²+Dх+Еy+F=0 (14)

Такое преобразование приводит ее к виду:

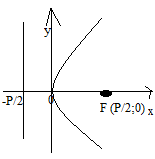
y²=2pх (15)

точка F()-фокус фокусом параболы, а прямая х=--директрисой параболы.