
- •Тема1. Матрицы и определители (4ч)
- •Доказательство:
- •Свойства определителей:
- •Обратная матрица.
- •Алгоритм вычисления обратной матрицы:
- •Ранг матрицы.
- •Элементарные преобразование матрицы:
- •Тема 2. Системы линейных уравнений. (1ч.)
- •Теорема Крамера.
- •Теорема Кронекера-Капелли.
- •Тема 4. Линейные операторы
- •Тема 5. Квадратные формы. (1ч.)
- •Решение:
- •Уравнение прямой
- •Общее уравнение прямой.
- •Уравнение плоскости.
Теорема Кронекера-Капелли.
Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Без доказательства.
Для совместных систем линейных уравнений верны:
1) Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система (1) имеет единственное решение.
2) Если ранг матрицы совместной системы меньше числа переменных, т.е. r<n, то система (1) неопределенная и имеет бесконечное множество решений.
Пусть r < n, r переменных х1, х2, …, хr называются основными или базисными, если определитель матрицы иэ коэффициентов при них отличен от нуля. Остальные n – r называются неосновными (или свободными).
Решение системы (1), в котором все n – r неосновных переменных равны нулю, называется базисным.
Система линейных однородных уравнений имеет ненулевые решения, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r(А) < n.
Рассмотрим процесс производства за год:
Хi- общий объем продукции i-й отрасли.
Хij- объем продукции i-й отрасли, потребляемой j-й отраслью.
Yi- объем конечного продукта i-й отрасли.
Хi
=
![]() +yi
(i=
1,2….n)
(5)
+yi
(i=
1,2….n)
(5)
Уравнение (5) называется соотношениями баланса. Введем коэффициенты прямых затрат:
Аij
=
![]() (6)
(6)
Показывающие затраты продукции i-й отрасли на производство продукции j-й отрасли.
Хij = аijхj (7)
Тогда модель межотраслевого баланса называется линейной. (5) примут вид:
![]() (8)
(8)
Х=АХ + Y (9)
Основная задача межотраслевого баланса состоит в отыскании такого вектора выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
(Е-А)Х = Y; Х = (Е-А)-1Y – модель Леонтьева
Тема 3. Векторные пространства. (3+1ч)
 Определение.
n
– мерным вектором называется упорядоченная
совокупность n
действительных чисел, записываемых в
виде х (х1,…,хn)
Определение.
n
– мерным вектором называется упорядоченная
совокупность n
действительных чисел, записываемых в
виде х (х1,…,хn)
 Два
n
– мерных вектора равны только тогда,
когда равны их соответствующие компоненты.
Два
n
– мерных вектора равны только тогда,
когда равны их соответствующие компоненты.

 Вектором
называется
направленный отрезок АВ. Длиной │АВ│
вектора АВ называется число, равное
длине отрезка АВ.
Вектором
называется
направленный отрезок АВ. Длиной │АВ│
вектора АВ называется число, равное
длине отрезка АВ.
Вектора называются коллинеарными, если существует прямая, которой они параллельны. Обозначается О = АА – нулевой вектор.
П


 роизведением
вектора а на числоλ
называется вектор b
= λа,
имеющий длину
роизведением
вектора а на числоλ
называется вектор b
= λа,
имеющий длину
│ b│=
│λ│а│,
направление которого совпадает с
направление вектора а, если λ
>0, и противоположно ему, если λ
<0.
b│=
│λ│а│,
направление которого совпадает с
направление вектора а, если λ
>0, и противоположно ему, если λ
<0.
Противоположным
вектором ![]() называется
произведение
называется
произведение ![]() на (-1).
на (-1).
Сумма
двух
векторов ![]() находится
по правилам треугольника и параллелограмма.
находится
по правилам треугольника и параллелограмма.

![]()
![]()


![]()

![]()


![]()
Правило треугольника Правило параллелограмма
Разностью
двух
векторов ![]() и
и
![]() называется
сумма вектора
называется
сумма вектора ![]() и
вектора
и
вектора ![]() .
.
Координатами
вектора ![]() называются
координаты его конечной точки.
называются
координаты его конечной точки.

![]()
![]()
![]()
Определение.
Скалярным
произведением ![]() двух векторов
двух векторов ![]() называется
число, равное произведению длин этих
векторов на косинус угла
называется
число, равное произведению длин этих
векторов на косинус угла ![]() между
ними:
между
ними:
![]()
![]() (1)
(1)
![]() (2)
(2)
![]() (2а)
(2а)
 (3)
(3)
Суммой
двух векторов
размерности n
называется
вектор ![]() ,
компоненты которого равны сумме
соответствующих компонент слагаемых
векторов.
,
компоненты которого равны сумме
соответствующих компонент слагаемых
векторов.
Произведением
вектора х на число ![]() называется
вектор
называется
вектор ![]() ,
компоненты которого равны произведению
,
компоненты которого равны произведению
![]() на
соответствующие компоненты вектора
на
соответствующие компоненты вектора
![]() .
.
Линейные операции над векторами удовлетворяют свойствам:
 +
+ =
= +
+ —
коммутативное свойство;
—
коммутативное свойство;(
 +
+ )+
)+ =
= +(
+( +
+ )
— ассоциативное
свойство;
)
— ассоциативное
свойство; — ассоциативное относительно
числового множителя свойство;
— ассоциативное относительно
числового множителя свойство;
4. ![]() —
дистрибутивное
относительно суммы векторов свойство;
—
дистрибутивное
относительно суммы векторов свойство;
5.
![]() — дистрибутивное относительно суммы
числовых множителей свойство;
— дистрибутивное относительно суммы
числовых множителей свойство;
Существует (
 нулевой вектор
нулевой вектор  =(0,0,...,0)
такой, что
=(0,0,...,0)
такой, что  ;
;Для любого вектора
 существует
(
существует
(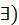 противоположный вектор (
противоположный вектор (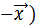 такой,
что
такой,
что  ;
; .
.
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее свойствам 1) – 8), называется векторным пространством.
Если под х, у, z рассматриваются векторы любой природы то соответствующее множество элементов называется линейным пространством.
Определение.
Вектор
![]() называется линейной
комбинацией векторов
называется линейной
комбинацией векторов ![]() векторного пространства R,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
векторного пространства R,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
![]() (4)
(4)
Определение.
Векторы
![]() векторного пространства R
называются линейно
зависимыми, если
существуют такие числа
векторного пространства R
называются линейно
зависимыми, если
существуют такие числа ![]() ,
не
равные одновременно 0, что
,
не
равные одновременно 0, что
![]() (5)
(5)
В
противном случае векторы ![]() называются линейно
независимыми.
называются линейно
независимыми.
Определение. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых векторов.
Определение. Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.
Теорема. Каждый вектор х линейного пространства R можно представить
и притом единственным способом в виде линейной комбинации векторов базиса.
Док-во:
![]() (6)
(6)
Числа
![]() - координаты вектора х относительно
этого базиса.
- координаты вектора х относительно
этого базиса.
Пусть
в пространстве R
имеются
два базиса: старый
![]() и
новый
и
новый ![]() .
.
 (7)
(7)
Переход от старого базиса к новому задается матрицей перехода
.
![]()
Пусть
![]()
![]() и
и
![]()
![]() относительно
нового базиса.
относительно
нового базиса.
![]() (8)
(8)
Подставив из (7), получим
 (9)
(9)
Определение.
Скалярным
произведением двух
векторов ![]() и
и ![]() называется число
называется число
![]() (10)
(10)
Скалярное произведение имеет свойства:
(
 ,
,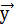 )
=
(
)
=
( ,
, )
— коммутативное
свойство;
)
— коммутативное
свойство;
(
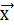 ,
,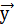 +
+ )
= (
)
= ( ,
, )+(
)+( ,
, )
— дистрибутивное
свойство;
)
— дистрибутивное
свойство;(
 ,
, )=
)=
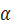 (
( ,
, );
);(
 )>0.
)>0.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее свойствам 1) – 4), называется евклидовым пространством.
Длиной
(нормой) вектора
![]() в евклидовом пространстве называется
корень квадратный из его скалярного
квадрата:
в евклидовом пространстве называется
корень квадратный из его скалярного
квадрата:
![]() (11)
(11)
Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Векторы
![]() n-мерного
евклидова пространства образуют
ортонормированный
базис, если
эти векторы попарно ортогональны и
норма каждого из них равна единице.
n-мерного
евклидова пространства образуют
ортонормированный
базис, если
эти векторы попарно ортогональны и
норма каждого из них равна единице.
