
Статистика
.pdf
2.(18) Какой из двух показателей растет быстрее: выручка или прибыль
от продаж? Как изменилась за полгода рентабельность продаж?
Месяцы |
Янв. |
Фев. |
март |
Апр. |
май |
Июнь |
|
|
|
|
|
|
|
Выручка от |
30 |
31 |
33 |
36 |
35 |
34 |
продаж, млн. руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Прибыль от |
1,50 |
1,54 |
1,59 |
2,10 |
2,25 |
2,30 |
продаж, млн. руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
1)Рассчитаем темпы роста выручки и прибыли от продаж по формуле:
отношение уровня месяца к уровню предыдущего месяца
Полученные значения представим в таблице:
Месяцы |
Янв. |
Фев. |
март |
Апр. |
май |
Июнь |
|
|
|
|
|
|
|
Выручка от |
30 |
31 |
33 |
36 |
35 |
34 |
продаж, млн. руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Темп роста, % |
- |
103,3 |
106,5 |
109,1 |
97,2 |
97,1 |
|
|
|
|
|
|
|
Прибыль от |
1,50 |
1,54 |
1,59 |
2,10 |
2,25 |
2,30 |
продаж, млн. руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Темп роста, % |
- |
102,7 |
103,2 |
132,1 |
107,1 |
102,2 |
|
|
|
|
|
|
|
Рентабельность |
5,00 |
4,97 |
4,82 |
5,83 |
6,43 |
6,76 |
продаж, % |
|
|
|
|
|
|
|
|
|
|
|
|
|
Как показывают рассчитанные темпы роста, прибыль от продаж растет быстрее выручки от продаж.
2)
ПР – прибыль от продаж ВР – выручка от продаж
Рассчитанные значения представлены в таблице.

Таким образом, рентабельность от продаж за полгода выросла на
35,2% ( )
3. (20) |
Имеются следующие данные, млрд. руб. |
|
|||
|
|
|
|
|
|
Кварталы |
|
Объем промышленной продукции в РФ |
|||
|
|
|
|
|
|
|
|
2000 г. |
|
2001 г. |
2002 г. |
|
|
|
|
|
|
I |
|
1180,0 |
|
1250,6 |
1400,3 |
II |
|
1200,0 |
|
1222,0 |
1500,3 |
III |
|
1306,0 |
|
1400,1 |
1565,4 |
IV |
|
1440,8 |
|
1550,5 |
1605,3 |
|
|
|
|
|
|
1. Определите индексы сезонности производства объема промышленной
продукции:
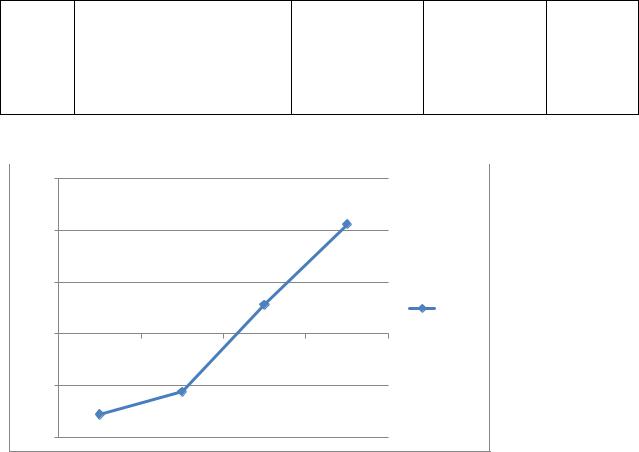
2. Постройте график сезонной волны.
Решение:
Индексы сезонности определим по формуле:
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||
где |
- значение объема продукции за квартал m года n |
|
||||||||
- среднемесячный объем продукции за год n |
|
|
||||||||
N – количество анализируемых лет = 3 |
|
|
||||||||
Представим данные в таблице: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Кварта |
Объем промышленной |
Средний |
Коэффициен |
Пики |
||||||
лы |
продукции в РФ |
|
объем |
ты |
сезоннос |
|||||
|
|
|
|
продукции по |
сезонности |
ти |
||||
|
|
|
|
кварталам |
|
|
||||
|
2000 г. |
2001 |
2002 г. |
|
|
|
|
|
|
|
|
|
г. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
1180,0 |
1250,6 |
1400,3 |
1276,97 |
0,922 |
-0,078 |
||||
II |
1200,0 |
1222,0 |
1500,3 |
1307,43 |
0,944 |
-0,056 |
||||
III |
1306,0 |
1400,1 |
1565,4 |
1423,83 |
1,028 |
0,028 |
||||
IV |
1440,8 |
1550,5 |
1605,3 |
1532,20 |
1,106 |
0,106 |
||||
Итого |
5126,8 |
5423,2 |
6071,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
варталь |
(5126,8+5423,2+6071,3)/1 |
|
||
ный |
|
2=1385,11 |
|
|
объем |
|
|
|
|
|
|
|
|
|
за 3 |
|
|
|
|
года |
|
|
|
|
Используя значения графы «Пики сезонности», построим график сезонной |
||||
волны |
|
|
|
|
0.15 |
|
|
|
|
0.1 |
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
Series1 |
0 |
|
|
|
|
|
I квартал |
II квартал |
III квартал |
IV квартал |
-0.05 |
|
|
|
|
-0.1 |
|
|
|
|
4. (22) |
Найти все недостающие значения показателей ряда динамики. |
|||
Годы |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Уровни ряда |
? |
? |
? |
50 |
? |
|
|
|
|
|
|
Абсолютные |
- |
? |
30 |
? |
? |
приросты |
|
|
|
|
|
(цепные) |
|
|
|
|
|
|
|
|
|
|
|
Темпы роста |
- |
1,5 |
? |
? |
? |
(цепные) |
|
|
|
|
|
|
|
|
|
|
|
Темпы роста |
- |
? |
? |
2,1 |
? |
(базисные) |
|
|
|
|
|
|
|
|
|
|
|
Среднегодовой темп роста составляет 1,4.
Решение:
Рассчитаем уровень ряда для первого года, исходя из данных за 4 год:

Темп роста базисный рассчитывается как отношение уровня года к уровню
базового года (обычно первого) по формуле: . Отсюда
Уровень ряда для второго года определим как произведение уровня ряда для первого года и темпа роста (цепного):
Уровень ряда для третьего года определим как сумму уровня ряда второго года и абсолютного цепного прироста для третьего ряда:
Так как среднегодовой темп роста равен 1,4, а годов пять, то определим темп роста базисный для пятого года:
Теперь определим уровень ряда для 5 года как произведение темпа роста базисного для 5 года и уровня ряда для первого года:
Рассчитаем оставшиеся показатели динамики по общеизвестным формулам: цепной абсолютный прирост:
=
=
=
=
цепной темп роста:
базисный темп роста:

Годы |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Уровни ряда |
23,8 |
35,7 |
65,7 |
50 |
91,4 |
|
|
|
|
|
|
Абсолютные |
- |
11,9 |
30 |
-15,7 |
41,4 |
приросты |
|
|
|
|
|
(цепные) |
|
|
|
|
|
|
|
|
|
|
|
Темпы роста |
- |
1,5 |
1,8 |
0,8 |
1,8 |
(цепные) |
|
|
|
|
|
|
|
|
|
|
|
Темпы роста |
- |
1,5 |
2,8 |
2,1 |
3,8 |
(базисные) |
|
|
|
|
|
|
|
|
|
|
|
5. (16) Построить прогноз показателя ряда динамики на 6-ой год по линейному тренду, рассчитанному методом наименьших квадратов.
Годы |
1 |
2 |
3 |
4 |
|
5 |
|
|
|
|
|
|
|
Показатель |
20 |
30 |
40 |
51 |
|
50 |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
Чтобы найти |
параметры |
линейного тренда |
y(t)=a0 |
+a1t, необходимо |
||
решить систему нормальных уравнений
Для расчета параметров методом наименьших квадратов (МНК) составим расчетную таблицу:

Годы |
t |
Показатель |
t2 |
yt |
|
|
y |
|
|
1 |
1 |
20 |
1 |
20 |
2 |
2 |
30 |
4 |
60 |
3 |
3 |
40 |
9 |
120 |
4 |
4 |
51 |
16 |
204 |
5 |
5 |
50 |
25 |
250 |
Итого |
15 |
191 |
55 |
654 |
Вычислим параметры:
Таким образом, уравнение линейного тренда имеет вид: y(t)=13,9 +8,1t
Построим прогноз показателя ряда динамики на 6 год: y(6)=13,9 +8,1∙6=62,5
Ответ: прогнозный уровень ряда 6-го года равен 62,5.
6. (15) Вывести аналитическое выражение тренда для ряда динамики по среднему темпу роста.
Периоды |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Уровни ряда |
40 |
45 |
55 |
60 |
61 |
|
|
|
|
|
|
Решение:
Вычислим средний темп роста по формуле:
Аналитическое выражение тренда для данного ряда динамики будет иметь вид:

Периоды |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Уровни ряда |
40 |
45 |
55 |
60 |
61 |
|
|
|
|
|
|
Тренд |
40 |
44 |
49 |
54 |
60 |
|
|
|
|
|
|
7. (20) Найти и сравнить коэффициенты вариации выручки и прибыли от продаж по пяти организациям.
Организации |
Выручка, млн. руб. |
Прибыль, млн. руб. |
|
|
|
1 |
130 |
31 |
|
|
|
2 |
100 |
30 |
|
|
|
3 |
110 |
32 |
|
|
|
4 |
105 |
15 |
|
|
|
5 |
120 |
20 |
|
|
|
Решение:
Вычислим среднее значение по формуле средней арифметической:
где – значение вариант
n – общее число вариант (объем выборки) Средняя выручка равна:
Средняя прибыль равна:
Для расчета среднего квадратического отклонения и коэффициента вариации составим вспомогательную таблицу

Организации |
Выручка, млн.руб. |
Прибыль, млн.руб. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
130 |
289 |
31 |
29,16 |
|
|
|||
|
|
|
|
|
2 |
100 |
169 |
30 |
19,36 |
|
|
|||
|
|
|
|
|
3 |
110 |
9 |
32 |
40,96 |
|
|
|||
|
|
|
|
|
4 |
105 |
64 |
15 |
112,36 |
|
|
|||
|
|
|
|
|
5 |
120 |
49 |
20 |
31,36 |
|
|
|||
|
|
|
|
|
Итого |
|
580 |
|
233,2 |
|
|
|
|
|
Среднее квадратическое отклонение рассчитывается по формуле:
σх =
σчка =
σл =
Коэффициент вариации рассчитаем по формуле:
V =
= |
|
|
|
= 9,5% |
|
|
|
||
= |
|
|
= 26,7% |
|
|
||||
Коэффициент вариации прибыли превышает коэффициент вариации выручки, это говорит о более высокой колеблемости значений прибыли,
нежели значений выручки. Однако, оба коэффициенты вариации не превышают 33,3%, что говорит об однородности совокупностей.

Корреляционная связь
1.(20) Имеются следующие данные об уровне энерговооруженности
труда и себестоимости продукции:
Энерговооруженность труда, |
40 |
43 |
50 |
51 |
54 |
кВт |
|
|
|
|
|
|
|
|
|
|
|
Себестоимость 1 ед. продукции |
15 |
16 |
18 |
11 |
10 |
тыс. руб. |
|
|
|
|
|
|
|
|
|
|
|
1.Рассчитайте параметры линейного уравнения зависимости себестоимости продукции от энерговооруженности труда.
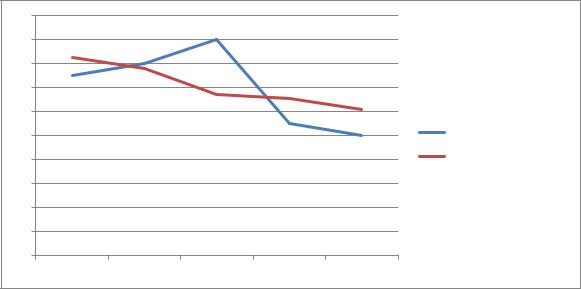
2.Покажите эмпирические и теоретические линии регрессии на графике.
Решение:
Чтобы найти параметры линейного тренда y(t)=a0 +a1t, необходимо решить
систему нормальных уравнений
Для расчета параметров составим расчетную таблицу:
№,п/п |
t |
Показатель |
t2 |
y∙t |
y(t) |
|
|
y |
|
|
|
1 |
40 |
15 |
1600 |
600 |
16,52 |
2 |
43 |
16 |
1849 |
688 |
15,59 |
3 |
50 |
18 |
2500 |
900 |
13,42 |
4 |
51 |
11 |
2601 |
561 |
13,11 |
5 |
54 |
10 |
2916 |
540 |
12,18 |
Итого |
238 |
70 |
11466 |
3289 |
70,82 |
Вычислим параметры:
Таким образом, уравнение линейного тренда имеет вид: y(t)=28,92 -0,31∙t
Так как коэффициент при t отрицательный, то наблюдается обратная связь, т.е. с увеличением величины энерговооруженности, себестоимость продукции снижается и наоборот.
20 |
|
|
|
|
18 |
|
|
|
|
16 |
|
|
|
|
14 |
|
|
|
|
12 |
|
|
|
|
10 |
|
|
|
|
8 |
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
Эмпирическая линия
Линия тренда
2. (22) Имеются следующие данные по группе предприятий:
№ предприятия |
Основные производственные |
Объем продукции, млн. |
п/п |
фонды, млн. руб. |
руб. |
1 |
4 |
8 |
2 |
5 |
6 |
3 |
6 |
10 |
4 |
10 |
9 |
5 |
12 |
12 |
По исходным данным определите линейное уравнение корреляционной связи между размером основных фондов и выпуском продукции
Решение:
Чтобы найти параметры линейного тренда y(t)=a0 +a1t, необходимо решить
систему нормальных уравнений
Для расчета параметров составим расчетную таблицу:
|
Основные |
Объем |
|
|
№,п/п |
производственные |
продукции, |
t2 |
y∙t |
|
фонды, млн. руб. |
млн. руб. |
|
|
|
t |
y |
|
|
1 |
4 |
8 |
16 |
64 |
2 |
5 |
6 |
25 |
36 |
3 |
6 |
10 |
36 |
100 |
4 |
10 |
9 |
100 |
81 |
5 |
12 |
12 |
144 |
144 |
Итого |
37 |
45 |
321 |
425 |
