
- •«Финансовый университет при правительстве
- •Содержание
- •Введение
- •1. Краткие теоретические сведения о маи
- •1.1. Собственные векторы и собственные значения матрицы
- •1.2. Алгоритм маи
- •1.2.1. Основные положения
- •Основные принципы метода анализа иерархий
- •1.2.2. Постановка задачи (пример)
- •1.2.3. Этапы маи
- •3. Ограничения на область применимости маи
- •Вопросы для самоподготовки:
- •4. Порядок выполнения лабораторной работы
- •Варианты заданий Базовый вариант задания (№0)
- •Литература:
- •Горбатков Станислав Анатольевич
1. Краткие теоретические сведения о маи
1.1. Собственные векторы и собственные значения матрицы
Прежде, чем изложить подробно алгоритм МАИ и описать пример его применения, приведем элементарные сведения о понятиях «собственный вектор» (СВ) матрицы и ее «собственное значение» (СЗ), поскольку МАИ основан на использовании этих понятий и математическим аппарате линейной алгебры.
Определение.
Число λ
называется собственным значением (или
характеристическим числом) квадратной
матрицы А
порядка n,
если можно подобрать такой n-мерный
нулевой вектор
![]() ,
что выполняется уравнение [10, с. 70]:
,
что выполняется уравнение [10, с. 70]:
![]() или
или
![]() .
(1)
.
(1)
Множество всех
собственных значений
![]() матрицы А находится как корни
характеристического или векового
уравнения
матрицы А находится как корни
характеристического или векового
уравнения
![]() ,
(2)
,
(2)
где λ – рассматривается в качестве независимых переменных; Е – матричная единица; det(·) – определитель матрицы.
Замечание 1. Если выполнить операцию вычисления определителя det(·) в (2), то получим выражение для характеристического полинома относительно собственных чисел:
![]() .
(3)
.
(3)
Решение систем линейных однородных уравнений вида (1) и (2) основано на известной лемме из теории матриц [9, с. 54]: «Для того, чтобы линейная система однородных алгебраических уравнений имела нетривиальное решение, необходимо и достаточно равенство нулю ее определителя».
Пример. Найти собственные значения и собственные векторы матрицы
![]() .
.
Запишем характеристическое уравнение матрицы
![]() .
.
То есть получилось квадратное уравнение (характеристический многочлен) относительно неизвестных значений λ.
Решением этого квадратного уравнения будут корни:
![]() .
.
Найдем собственные векторы, принадлежащие собственным значениям. Собственный вектор принадлежащий собственному значению
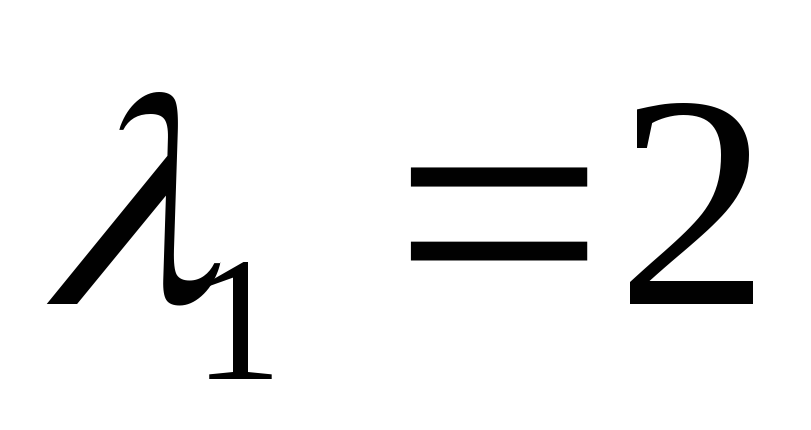 ,
по определению является нулевым решением
системы
,
по определению является нулевым решением
системы
![]() .
(3)
.
(3)
Верхний индекс в
скобках означает принадлежность к
собственному значению
![]() ,
а нижний индекс – это номер простого
(не кратного) корня.
,
а нижний индекс – это номер простого
(не кратного) корня.
Поучим:
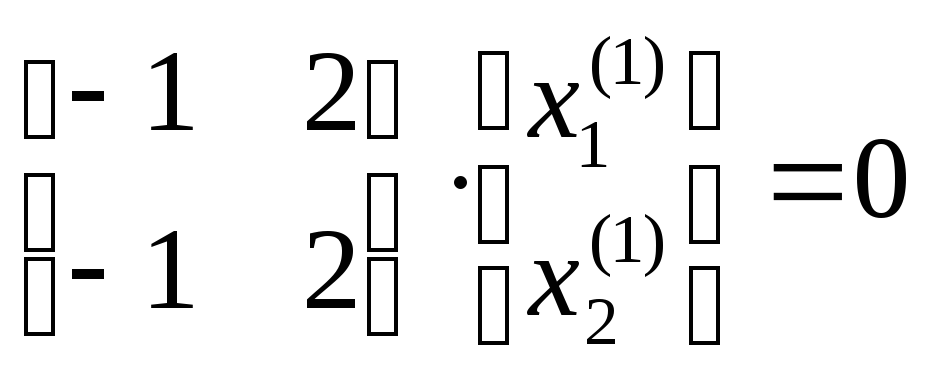 .
.
Проверяем условие цитированной выше леммы:
![]() .
.
Условия выполнены, значит нетривиальное решение (3) существует. Тогда в простейшем случае системы двух уравнений [9, с. 336]:
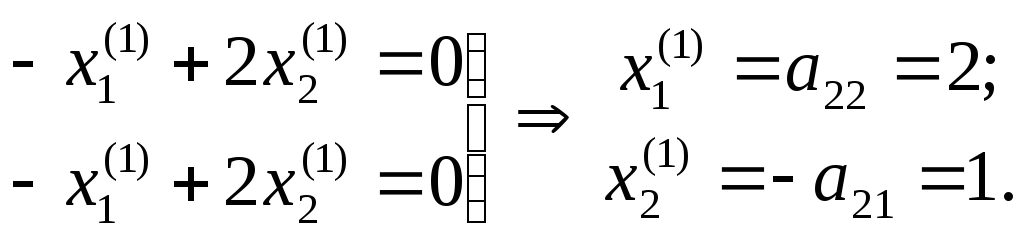
Таким образом,
ненулевой собственный вектор, принадлежащий
собственному числу
![]() ,
найден:
,
найден:
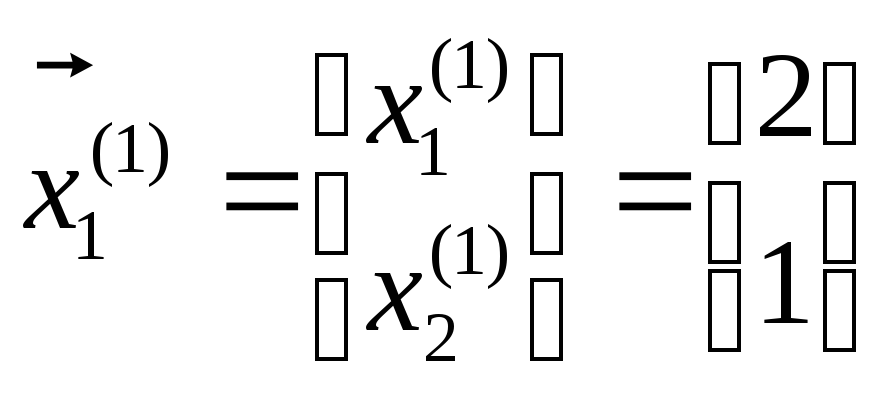 .
.
Аналогично
находится второй собственный вектор
![]() матрицыА,
принадлежащий собственному значению
матрицыА,
принадлежащий собственному значению
![]() .
.
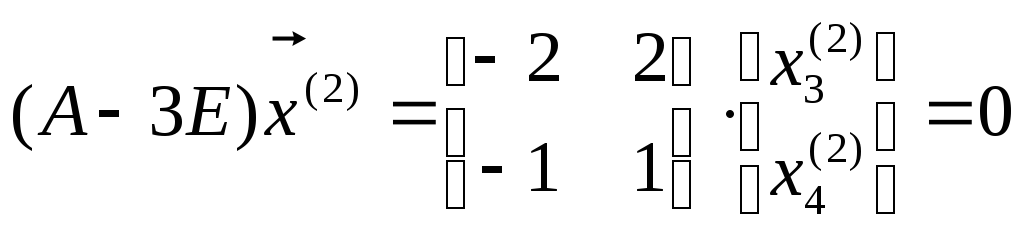 ;
;
![]()
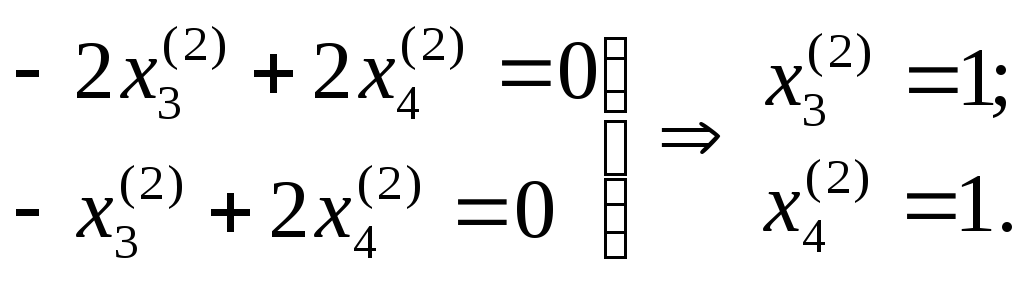
Следовательно,
второй собственный вектор, принадлежащий
собственному числу
![]() ,
равен
,
равен
![]() .
.
Замечание.
Метод нахождения собственных чисел
![]() и собственных векторов из [9, с. 336]
неэффективен с точки зрения вычислительной
математики при высоком порядке матрицыА
(n
~ сотни и тысячи).
и собственных векторов из [9, с. 336]
неэффективен с точки зрения вычислительной
математики при высоком порядке матрицыА
(n
~ сотни и тысячи).
В вычислительной математике известны различные вычислительные схемы определения собственных чисел и собственных векторов матрицы, и имеются соответствующие пакеты программ для ЭВМ. Однако до настоящего времени общепринятый стандартный простой метод решения проблемы на собственные значения и собственные векторы матриц большого размера отсутствует.
Если под рукой нет подходящей программы, то можно применить один из простых приближенных методов, описанных в [1, с. 32]. В лабораторной работе применен метод под номером 4, использующий среднегеометрическую оценку компонент собственного вектора (см. ниже, пункт 1.2).
