Интегрирование тригонометрических функций

Рассмотрим интеграл типа , гдеRобозначает рациональную функцию своих аргументови. Интеграл данного типа сводится к интегралу от рациональной функции с помощью так называемой универсальной постановки.

Действительно, и=.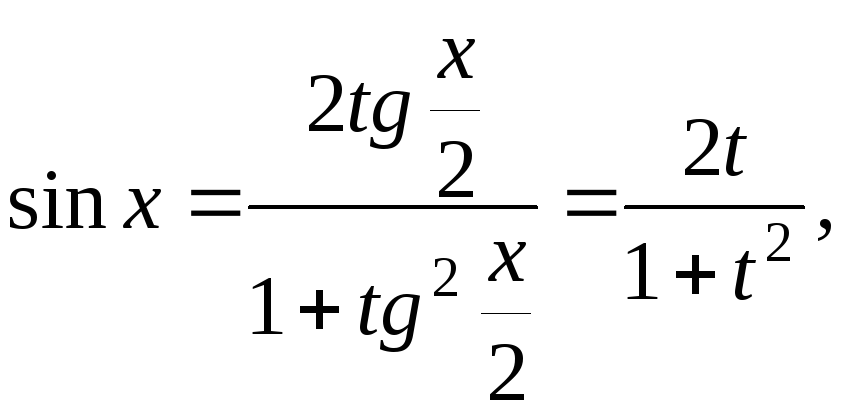

Тогда, подставляя в данный интеграл вместо ,иполученные выражения, будем иметь под знаком интеграла рациональную функцию.

Пример13.Вычислить интеграл.

Решение. Подстановкадает:

==.

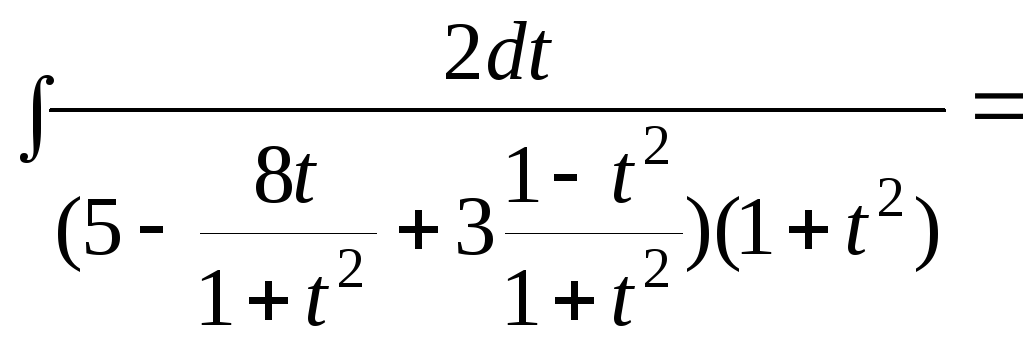
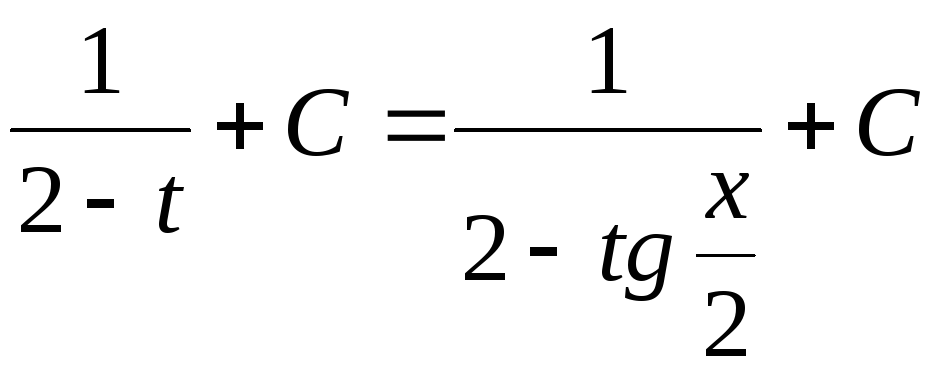Универсальная подстановка нередко приводит к сложным вычислениям. Поэтому в указанных ниже случаях предпочтительней частные подстановки, также рационализирующие интеграл.

если , то применима подстановка;

если , то применима подстановка;

если , то применима подстановка.

Пример14. Вычислить интеграл.

Решение. Положими найдем:

поэтому:

===.

Рассмотрим интеграл вида , гдеmиn-целые числа. Возможны следующие случаи:

1. Одно из чисел mилиn– нечетное, например, тогда полагая, получим:

==

2. Оба числа mиn– четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:

.

Пример15. Вычислить интеграл.

Решение. ==.

Интегрирование некоторых иррациональных функций

Рассмотрим интеграл следующего вида: ,

где R- рациональная функция,- рациональные числа. Данный интеграл сводится к интегралу от рациональной функции с помощью подстановки, гдеk- общий знаменатель всех дробных показателей.

Пример16.Вычислить интеграл.

Решение. Положив, получим:===.

Контрольные задания

Вычислить неопределенные интегралы.

5.1

5.2 .

5.3 .

5.4 .

5.5 .

5.6 .

5.7 .

5.8 .

5.9 .

5.10 .

5.11 .

5.12 .

5.13 .

5.14 .

5.15 .

5.16 .

5.17 .

5.18 .

5.19 .

5.20 .

Указания к заданию 6 тема 6. Определенный интеграл

Пусть функция определена на отрезке. Разобьем этот промежуток произвольным образом наnчастей точками .

В каждом из полученных частичных промежутков , где, выберем произвольную точку. Вычислим значение функциии умножим его на разность, после этого составим сумму, которая называетсяинтегральной суммой Римана для функциина отрезке.

Пусть , т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммыпри, не зависящий ни от способа разбиения промежуткана части, ни от выбора точек, то этот предел называетсяопределенным интеграломфункциина промежуткеи обозначается символом. Таким образом,.

Функция в этом случае называетсяинтегрируемойв промежутке. Числаиназываются соответственно нижним и верхним пределами интеграла.

Выясним геометрический смысл суммы Римана , когда функциянепрерывна и неотрицательна в промежутке,. В этом случае произведениеравно площади прямоугольника с основаниеми высотой, а суммаравна сумме площадей прямоугольников с основаниеми высотами(рис. 1).

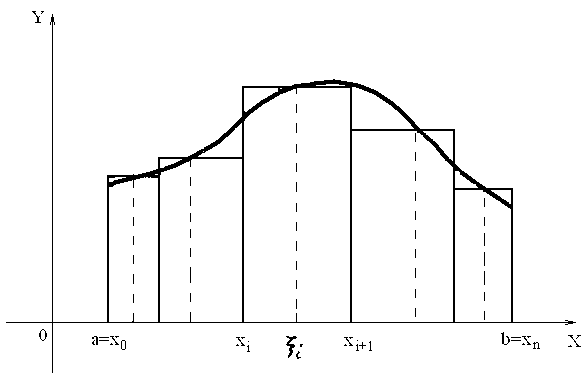
Рис.1

Таким образом, равна площади ступенчатой фигуры, а определенный интеграл равен пределупри, т.е. площади криволинейной трапеции, ограниченной графиком функции, прямымиии отрезкомоси.

Свойства определенного интеграла

Пусть все рассматриваемые функции являются непрерывными, так что определенные интегралы от них существуют. Тогда справедливы следующие соотношения:

1.

2.

3.

4.

5.

6. Если .

Если функции непрерывна на отрезкеи- какая-нибудь первообразная дляна этом отрезке, то справедлива формула Ньютона-Лейбница:

.

Правую часть формулы часто обозначают символом (знак двойной подстановки отдо).

Пример1. Вычислить определенный интеграл.

Решение. .

Замена переменной в определенном интеграле

Пусть функция непрерывна на отрезке, а функцияопределена и непрерывна вместе со своей производнойна отрезке, причемдля любогои,

Тогда:

Эта формула называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой.

Пример2.Вычислить определенный интеграл.

Решение.Сделаем замену переменной.

Тогда . Пересчитаем пределы интегрирования: при, а при.

.

Заметим, что при вычислении определенного интеграла к старой переменной не возвращаются.

Интегрирование по частям в определенном интеграле

Теорема. Если функции идифференцируемы на отрезке, то справедлива следующая формула.

Пример3. Вычислить.

Решение. Обозначим,.

Тогда ,.

.

Геометрические приложения определенного интеграла

Площадь плоской фигуры

Площадь криволинейной трапеции, ограниченной графиком, осьюи прямымии(рис.2) вычисляется по следующей формуле:

Если часть кривой находится под осью(рис.3), то площадь заштрихованной фигуры равна:

.

Пусть фигура ограничена двумя кривыми ,

и,(рис. 4). Тогда ее площадь вычисляется по формуле.

Рис.2

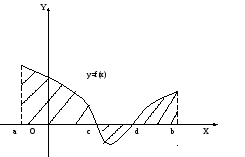
Рис. 3

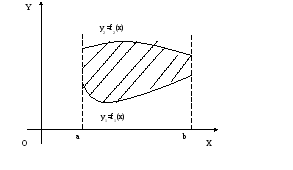
Рис. 4

Пример4.Вычислить площадь фигуры, ограниченной прямойи параболой.

Решение.Построим графики прямой и параболы

(рис. 5).

Рис. 5.

Найдем точки пересечения параболы и прямой:

.

Тогда получим:

.