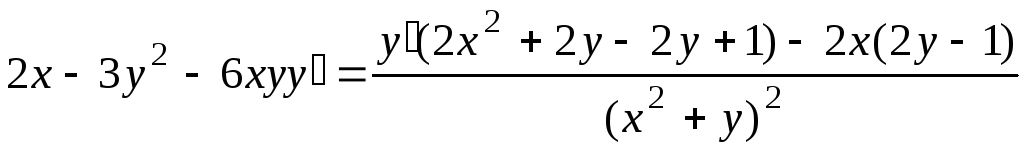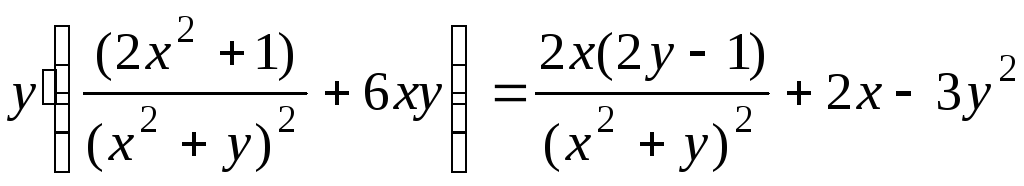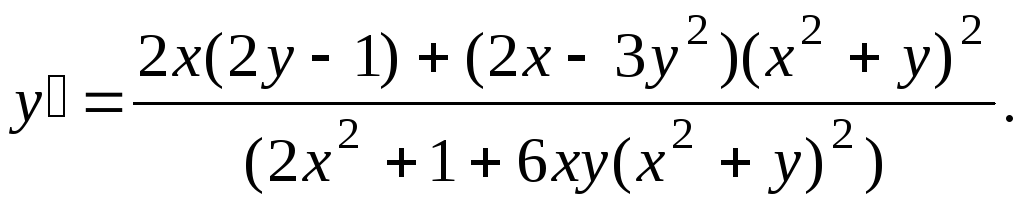- •Математика
- •Содержание
- •1. Общие положения
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №2 Указания к заданию 1
- •Тема 1. Предел функции
- •Контрольные задания
- •Указания к заданию 2
- •Тема 2. Основы дифференциального исчисления
- •Контрольные задания
- •Указания к заданию 3
- •Тема 3. Исследование функции и построение графика
- •Контрольные задания
- •Указания к заданию 4
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Указания к заданию 5 тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Контрольные задания
- •Указания к заданию 6 тема 6. Определенный интеграл
- •Свойства определенного интеграла
- •Объем тела вращения
- •Контрольные задания
- •Указания к заданию 7
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
- •Контрольные задания
- •Указания к заданию 8
- •Тема 8. Ряды
- •Рассмотрим выражение вида
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6. Список литературы
- •Содержание дисциплины
- •Раздел 1. Основы алгебры и анализа
- •Тема 1.3. Введение в анализ функций одной переменной.
- •Тема 1.4. Дифференциальное исчисление функции одной переменной.
- •Раздел 2. Функции нескольких переменных. Интегральное исчисление.
- •Тема 2.1. Функции нескольких переменных.
- •Тема 2.2. Неопределенный интеграл.
- •Тема 2.3. Определенный интеграл.
- •Раздел 3. Обыкновенные дифференциальные уравнения. Ряды.
- •Тема 3.1. Обыкновенные дифференциальные уравнения (оду).
- •Тема 3.2. Системы обыкновенных дифференциальных уравнений.
- •Тема 3.3. Числовые ряды.
- •Тема 3.4. Функциональные ряды.
- •Образец оформления титульного листа
Контрольные задания
Найти следующие пределы.
1.1
а) ![]() б)
б) ![]()
1.2.
а) ![]() б)
б) ![]()
1.3.
а)![]() б)
б) ![]()
1.4.
а) ![]() б)
б) 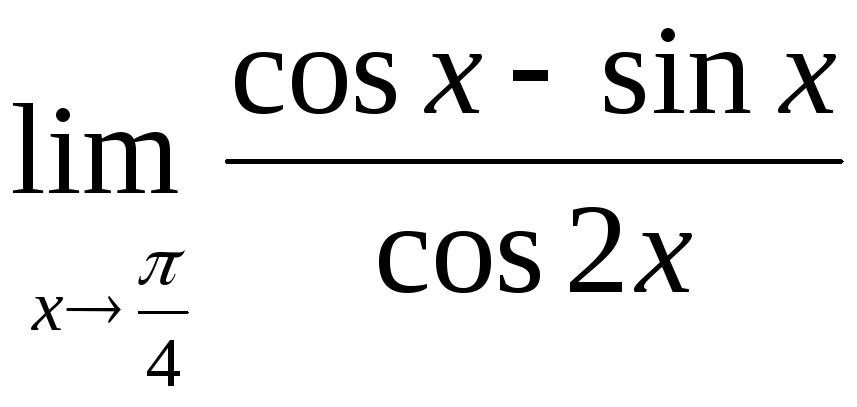
1.5.
а) б)
б)
![]()
1.6.
а) ![]() б)
б) 
1.7.
а) б)
б) 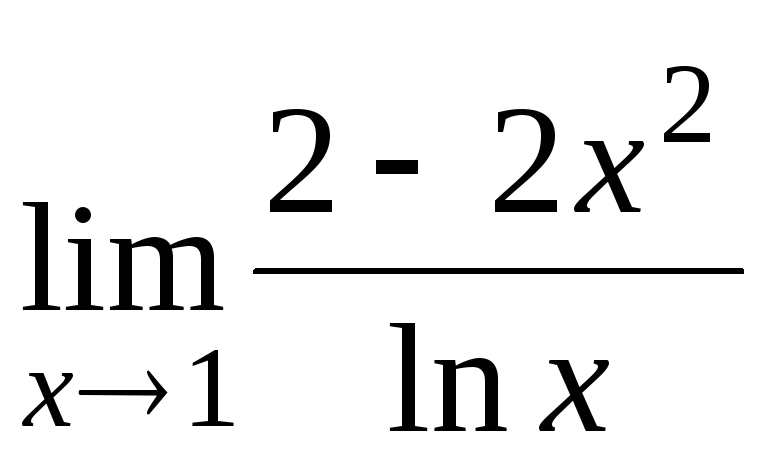
1.8.
а) ![]() б)
б) ![]()
1.9.
а) б)
б)
![]()
1.10.
а) ![]() б)
б) ![]()
1.11.
а)![]() б)
б)

1.12.
а) 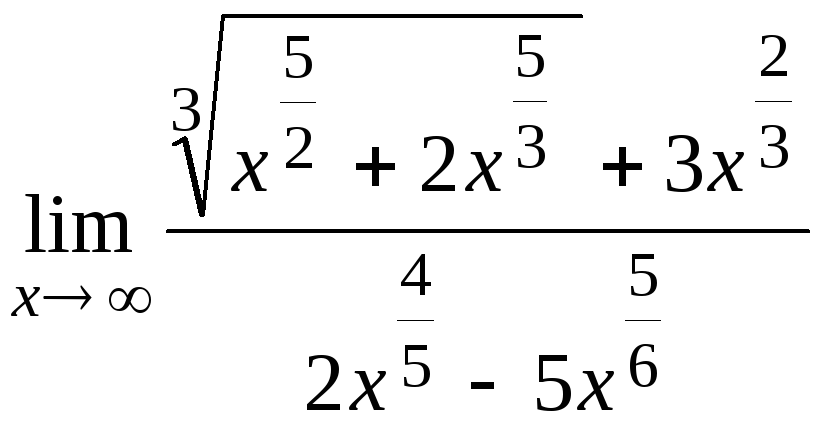 б)
б) ![]()
1.13.
а) б)
б)
![]()
1.14.
а) ![]() б)
б)
![]()
1.15.
а)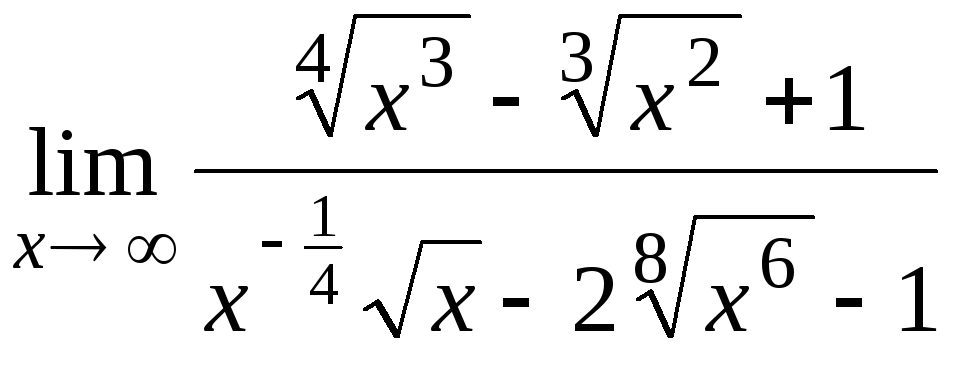 б)
б)
![]()
1.16.
а) ![]() б)
б) 
1.17.
а)![]() б)
б)
![]()
1.18.
а) ![]() б)
б) 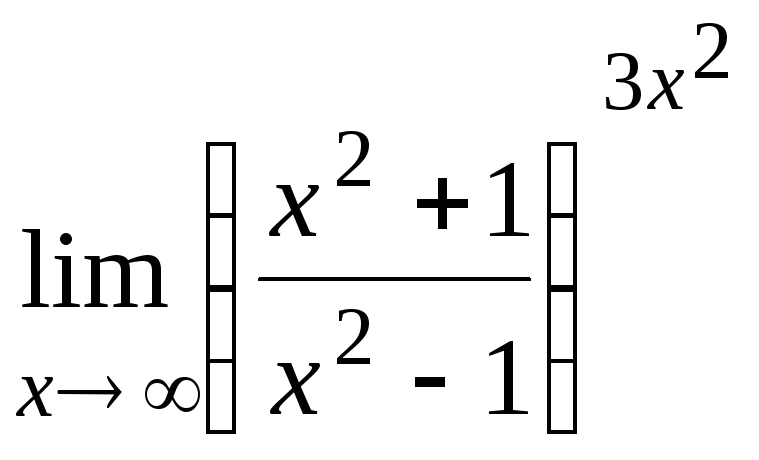
1.19.
а)![]() б)
б)
![]()
1.20.
а) ![]() б)
б) ![]()
Указания к заданию 2
Тема 2. Основы дифференциального исчисления
Пусть
на интервале
![]() задана функция
задана функция![]() .
Возьмем некоторое число
.
Возьмем некоторое число![]() и придадим аргументу
и придадим аргументу![]() приращение
приращение![]() .
Тогда значение функции получит приращение
.
Тогда значение функции получит приращение![]() .
Рассмотрим отношение
.
Рассмотрим отношение![]()
![]() .
Если при
.
Если при![]() существует конечный предел дроби
существует конечный предел дроби![]() ,
то этот предел называютпроизвoдной
функции
,
то этот предел называютпроизвoдной
функции
![]() в точке
в точке![]() и обозначают символом
и обозначают символом![]() (или
(или![]() ):
):
![]() .
.
Нахождение производной называют дифференцированием функции.
Функцию
![]() называютдифференцируемой
в точке
называютдифференцируемой
в точке
![]() ,
если в окрестности этой точки ее
приращение может быть представлено в
виде:
,
если в окрестности этой точки ее
приращение может быть представлено в
виде:
![]()
![]() .
.
Можно
доказать, что для дифференцируемости
функции необходимо и достаточно, чтобы
существовала и была конечной ее
производная, при этом
![]() .
.
Выражение
![]() называют
дифферен-циалом
функции и
обозначают
называют
дифферен-циалом
функции и
обозначают
![]() .
Приращение аргумента
.
Приращение аргумента![]() называют дифференциалом независимой
переменной и обозначают
называют дифференциалом независимой
переменной и обозначают![]() .
Таким образом,
.
Таким образом,
![]() .
.
Геометрически
дифференциал
![]() есть
приращение касательной, проведенной к
графику функции в точке
есть
приращение касательной, проведенной к
графику функции в точке
![]() ,
и может
быть как меньше, так и больше приращения
функции
,
и может
быть как меньше, так и больше приращения
функции
![]() .
Для линейной функции
.
Для линейной функции![]()
![]()
Если
производная существует для всех
![]() из интервала
из интервала![]() ,
то тем самым производная определена
как функция
,
то тем самым производная определена
как функция![]() в этом интервале, и можно говорить о
производной от этой функции, называемой
второй производной функции
в этом интервале, и можно говорить о
производной от этой функции, называемой
второй производной функции![]() :
:![]() Аналогично вводится понятие высших
производных (третья производная и т.д.)
Аналогично вводится понятие высших
производных (третья производная и т.д.)![]()
Для освоения техники дифференцирования, то есть нахождения производных, необходимо использовать правила дифференцирования и таблицу производных наиболее часто встречающихся функций.
Основные правила дифференцирования
1.
![]()
![]() .
.
2.
![]() (
(![]() –
постоянная)
–
постоянная)![]() .
.
3.
![]()
![]()
4.
![]()
![]() .
.
5.
Производная сложной функции: если
![]() ,
то
,
то![]() ,
где производные функций в правой части
равенства берутся по аргументам
,
где производные функций в правой части
равенства берутся по аргументам![]() и
и![]() соответственно.
соответственно.
Приведем таблицу производных наиболее часто используемых функций:
1.
![]() (
(![]() –
постоянная)
–
постоянная)![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]() (
(![]() –
постоянная)
–
постоянная)![]()
5.
![]()
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
![]()
![]()
14.
![]()
![]()
15.
![]()
![]()
Логарифмической
производной
функции
![]() называется
производная от логарифма этой функции:
называется
производная от логарифма этой функции:
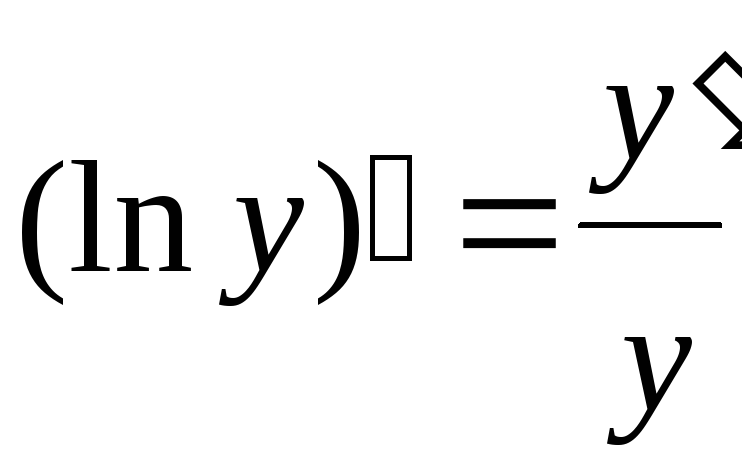 ,
при
y
> 0. Нахождение
производных от многих функций значительно
упрощается, если эти функции предварительно
прологарифмировать, а затем воспользоваться
логарифмической производной. При этом
логарифмическую производную применяют
формально, не учитывая, что формула
имеет смысл лишь при y
> 0.
,
при
y
> 0. Нахождение
производных от многих функций значительно
упрощается, если эти функции предварительно
прологарифмировать, а затем воспользоваться
логарифмической производной. При этом
логарифмическую производную применяют
формально, не учитывая, что формула
имеет смысл лишь при y
> 0.
Функция y(x) называется неявной, если зависимость между х и у выражена уравнением F(x,y)=0, неразрешенным относительно у.
Чтобы
найти производную от неявной функции,
надо данное уравнение продифференцировать,
считая у
функцией от х,
а затем полученное уравнение решить
относительно производной
![]() .
.
Рассмотрим примеры вычисления производных.
Пример1.
Найти производную функции
![]() .
.
Решение. Применяя правила 4,1 и таблицу производных, получим:
![]()
![]()
![]() .
.
Пример2.
Найти
![]() ,
если
,
если![]() .
.
Решение. Последовательно применяя правило дифференцирования сложной функции, получим:
![]()
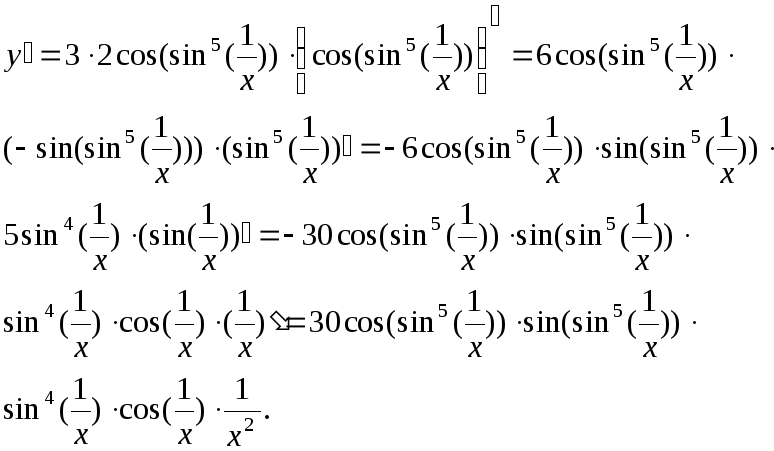
Пример3.
Найти
производную
функции
![]() .
.
Решение. Применим логарифмическую производную:
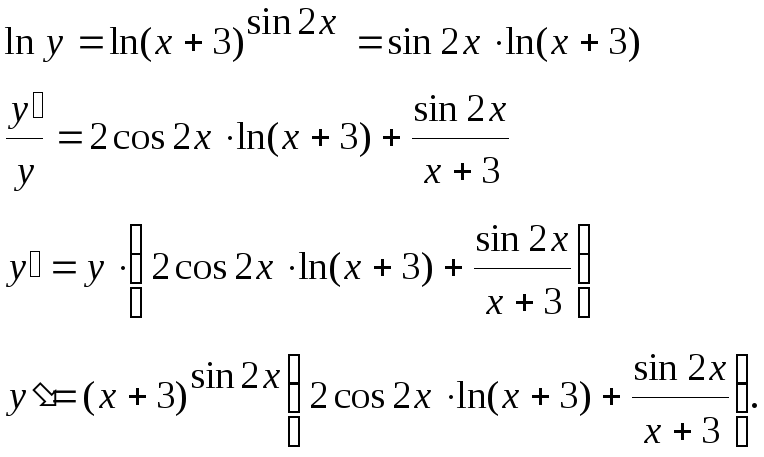
Пример4.
Найти
производную функции
 .
.
Решение. В случае произведения нескольких сомножителей применение логарифмической производной также эффективно:
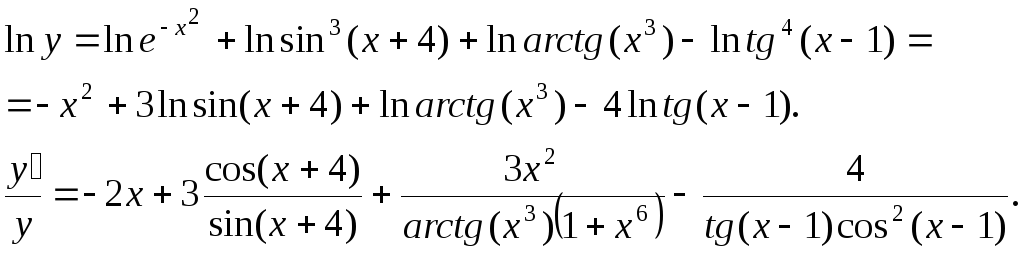
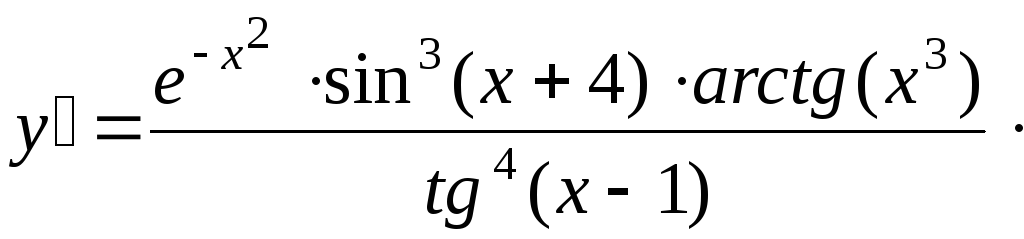 EMBED
Equation.3
EMBED
Equation.3
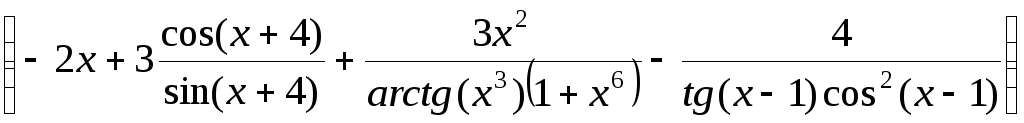 .Пример5.
Найти производную функции
.Пример5.
Найти производную функции
![]() ,
если
,
если![]() .
.
Решение. Применим правило дифференцирования неявной функции: