Matem_2_Komp_test
.docx
267@
A)
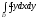
B)
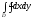
C)
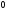
D)
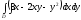
@268
Криволинейный
интеграл второго рода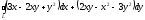
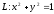 по
формуле Грина приводится к двойному
интегралу вида:
по
формуле Грина приводится к двойному
интегралу вида:
268@
A)
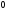
B)
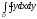
C)
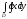
D)
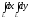
@269
Криволинейный
интеграл второго рода
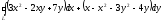
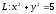 по формуле Грина приводится к двойному
интегралу вида:
по формуле Грина приводится к двойному
интегралу вида:
269@
A)
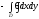
B)
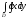
C)
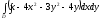
D)
@270
Криволинейный
интеграл второго рода
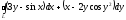 по
формуле Грина приводится к двойному
интегралу вида:
по
формуле Грина приводится к двойному
интегралу вида:
270@
A)
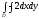
B)

C)
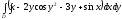
D)
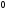
@271
Криволинейный интеграл второго рода по замкнутому контуру L, не зависящей от пути интегрирования есть:
271@
A)
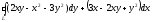
B)

C)
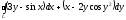
D)
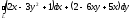
@272
Криволинейный интеграл второго рода по замкнутому контуру L, не зависящей от пути интегрирования, есть:
272@
A)
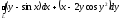
B)
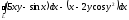
C)
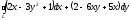
D)
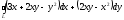
@273
Криволинейный интеграл второго рода по замкнутому контуру L, не зависящей от пути интегрирования, есть:
273@
A)
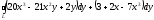
B)
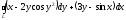
C)
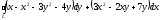
D)
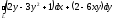
@274
Интеграл
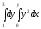 равен:
равен:
274@
A)
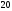
B)
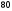
C)
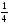
D)
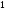
@275
Интеграл
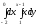 равен:
равен:
275@
A)
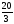
B)
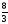
C)

D)

@276
Интеграл
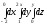 равен:
равен:
276@
A)
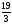
B)
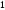
C)
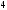
D)
@277
Интеграл
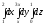 равен
равен
277@
A)
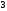
B)

C)
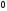
D)
@278
Поверхностной
интеграл первого рода
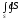 по поверхности
по поверхности
 в
виде двойного интеграла есть:
в
виде двойного интеграла есть:
278@
A)
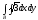
B)
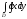
C)
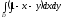
D)
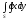
@279
Криволинейный
интеграл второго рода
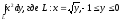 в
виде определенного интеграла есть:
в
виде определенного интеграла есть:
279@
A)
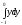
B)
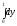
C)
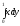
D) п.о.н.
@280
Криволинейный
интеграл
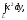 где
где
 равен:
равен:
280@
A)
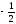
B)
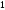
C)
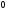
D)
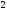
@281
Криволинейный
интеграл по замкнутому контуру L
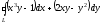 приводится к двойному интегралу вида:
приводится к двойному интегралу вида:
281@
A)
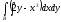
B)
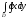
C)
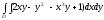
D)
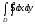
@282
Криволинейный
интеграл по замкнутому контуру L
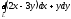 в
виде двойного интеграла есть:
в
виде двойного интеграла есть:
282@
A)
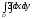
B)
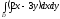
C)
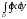
D)
@283
Длина
прямой
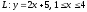 есть:
есть:
283@
A)
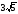
B)
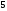
C)
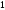
D)
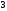
@284
Криволинейный
интеграл первого рода
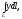 где
L
часть
окружности
где
L
часть
окружности
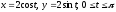 в
виде определенного интеграла есть:
в
виде определенного интеграла есть:
284@
A)
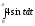
B)
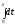
C)
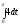
D)
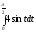
@285
Криволинейный
интеграл первого рода
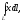 где
где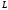 дуга
параболы
дуга
параболы
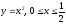 приводится к определенному вида:
приводится к определенному вида:
285@
A)
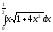
B)
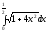
C)
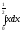
D)
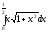
@286
Интеграл
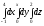 равен:
равен:
286@
A)
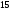
B)
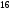
C)
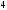
D)
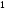
@287
Длина
прямой
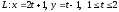 равна:
равна:
287@
A)
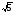
B)
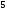
C)
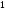
D)
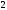
@288
Обьем
тела
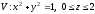 равен:
равен:
288@
A)
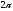
B)

C)
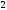
D)
@289
Площадь
области
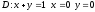 равна:
равна:
289@
A)
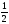
B)
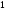
C)
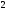
D)
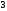
@290
Площадь
области
 равна;
равна;
290@
A)
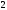
B)
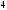
C)
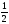
D)

@291
Площадь
области
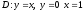 равна;
равна;
291@
A)
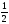
B)
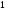
C)
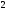
D)
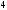
@292
Площадь
области
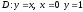 равна;
равна;
292@
A)
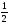
B)
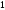
C)
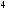
D)
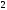
@293
Площадь
области
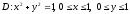 равна:
равна:
293@
A)
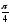
B)

C)
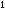
D)
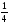
@294
Площадь
области
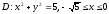 равна:
равна:
294@
A)
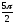
B)

C)
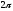
D)
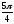
@295
После
замены порядка интегрирования интеграл
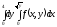 примет
вид:
примет
вид:
295@
A)
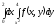
B)
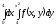
C)
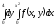
D)
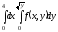
@296
После
замены порядка интегрирования интеграл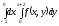 примет вид:
примет вид:
296@
A)
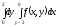
B)
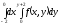
C)
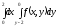
D)
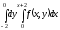
@297
Криволинейный
интеграл
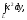 где
где
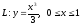 равен:
равен:
297@
A)
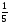
B)
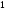
C)
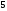
D)
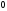
@298
Якобиан
перехода замены переменной
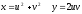 равен:
равен:
298@
A)
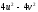
B)
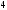
C)
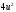
D)
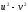
@299
Площадь
области
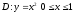 равна;
равна;
299@
A)
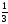
B)
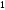
C)
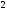
D)
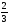
@300
Интеграл
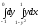 равен:
равен:
300@
A)
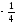
B)
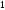
C)
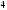
D)